

Мы поможем в написании ваших работ!
ЗНАЕТЕ ЛИ ВЫ?
|
Анализ текстовых парадоксов. . Языковые свойства имен объектов. . Пример 1. . Пример 2. . Пример 3.
Содержание книги
- Сущность языковых систем состоит в том, что закономерности мыслительных процессов реализуются в законах организации текстовых структур.
- Каковы закономерности знаковых систем, представляющих интеллектуальную продукцию в текстовой форме?
- О понятии действительных чисел
- Операции, определяющие формирование множества рациональных чисел.
- Аксиоматика рациональных чисел должна содержать правила, определяющие операции сложения, умножения, сравнения чисел и связь между этими операциями.
- Аксиома связи сложения и умножения.
- Задачи, приводящие к расширению множества рациональных чисел.
- Существуют числа, не являющиеся результатом конечного числа арифметических операций над целыми числами и не представимые в виде p/q ни для каких целых p, Q.
- О представлении действительных чисел.
- Аксиоматическое обоснование евклидовой геометрии.
- Аксиоматика Д. Гильберта(1862-1943)
- Группа 3. Аксиомы конгруэнтности.
- Теорема (о внешнем угле треугольника).
- Группа 4. Аксиомы непрерывности.
- Группа 5. Аксиома параллельности.
- Два недостатка аксиоматики Д. Гильберта.
- Структура векторного пространства.
- Множество всех векторов назовем векторным пространством, а построенную модель направленных отрезков - геометрической моделью векторного пространства.
- Если в пространстве задан базис { 1, 2, 3}, то между множеством векторов и упорядоченными тройками чисел (x,y,z) установлено взаимно-однозначное соответствие
- Абстрактное векторное пространство.
- Определение абстрактного векторного пространства.
- Аксиомы скалярного произведения векторов.
- Модель Вейля евклидовой геометрии.
- Свойства операции откладывания вектора.
- Многомерное арифметическое евклидово пространство.
- Модель А. Пуанкаре плоскости Лобачевского.
- Определение плоскости Лобачевского.
- Основные факты в планиметрии Лобачевского.
- Взаимное расположение прямых в плоскости L2.
- О роли открытия неевклидовой геометрии.
- Свойства аксиоматических систем.
- Понятие математической структуры.
- Модель или реализация системы аксиом.
- Формальная и содержательная аксиоматики. Теории и структуры.
- Другими словами, Изоморфизм моделей - это такое взаимно-однозначное соответствие между элементами моделей, которое сохраняет отношения элементов, задаваемые системой аксиом.
- Требования , предъявляемые к системам аксиом.
- Независимость аксиоматической системы.
- Независимость аксиомы параллельности.
- Определение (дедуктивной полноты).
- Историческая роль V постулата Евклида в развитии оснований математики.
- Анализ текстовых парадоксов. . Языковые свойства имен объектов. . Пример 1. . Пример 2. . Пример 3.
- Проблема выразимости.. Понятие искусственного языка.
- Парадокс достижимости в натуральном ряде.
§8 Анализ текстовых парадоксов.
8.1 Языковые свойства имен объектов.
Готлоб Фреге впервые обратил внимание на то, что имя каждого объекта имеет два значения: предметное и смысловое. Согласно его “теории смысла” с понятием имени связаны три отношения к объекту: предметное, смысловое и знаковое. Определим их:
Денотат имени - это предметное значение имени, т.е. сам именуемый объект.
Концепт имени - это смысловое значение имени, т.е. то объективное содержание, которое выражается именем.
Константы - это сами имена индивидуальных предметов, но не имена свойств и отношений.
Наличие у имен двух значений - предметного и смыслового, приводит к двузначности имени: если имеется в виду концепт имени, то говорят об интенциональном значении имени, если же имеется в виду денотат имени, то говорят об экстенциональном значении имени.
Рассмотрим примеры.
Пример 1.
“Число 2” - это имя имеет определенный денотат и концепт.
Пример 2.
Имена: “Отношение эквивалентности”, “подобие”, “параллельность” имеют определенный концепт, как некоторые отношения. В то же время денотаты этих имен не определены.
Пример 3.
Имя “ 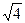 “ - символ, представляющий определенный денотат - число 2. Однако, его концепт неопределен: “ - символ, представляющий определенный денотат - число 2. Однако, его концепт неопределен: 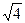 - операция или - операция или 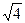 - величина? - величина?
|