Операции, определяющие формирование множества рациональных чисел.
Содержание книги
- Сущность языковых систем состоит в том, что закономерности мыслительных процессов реализуются в законах организации текстовых структур.
- Каковы закономерности знаковых систем, представляющих интеллектуальную продукцию в текстовой форме?
- О понятии действительных чисел
- Операции, определяющие формирование множества рациональных чисел.
- Аксиоматика рациональных чисел должна содержать правила, определяющие операции сложения, умножения, сравнения чисел и связь между этими операциями.
- Аксиома связи сложения и умножения.
- Задачи, приводящие к расширению множества рациональных чисел.
- Существуют числа, не являющиеся результатом конечного числа арифметических операций над целыми числами и не представимые в виде p/q ни для каких целых p, Q.
- О представлении действительных чисел.
- Аксиоматическое обоснование евклидовой геометрии.
- Аксиоматика Д. Гильберта(1862-1943)
- Группа 3. Аксиомы конгруэнтности.
- Теорема (о внешнем угле треугольника).
- Группа 4. Аксиомы непрерывности.
- Группа 5. Аксиома параллельности.
- Два недостатка аксиоматики Д. Гильберта.
- Структура векторного пространства.
- Множество всех векторов назовем векторным пространством, а построенную модель направленных отрезков - геометрической моделью векторного пространства.
- Если в пространстве задан базис { 1, 2, 3}, то между множеством векторов и упорядоченными тройками чисел (x,y,z) установлено взаимно-однозначное соответствие
- Абстрактное векторное пространство.
- Определение абстрактного векторного пространства.
- Аксиомы скалярного произведения векторов.
- Модель Вейля евклидовой геометрии.
- Свойства операции откладывания вектора.
- Многомерное арифметическое евклидово пространство.
- Модель А. Пуанкаре плоскости Лобачевского.
- Определение плоскости Лобачевского.
- Основные факты в планиметрии Лобачевского.
- Взаимное расположение прямых в плоскости L2.
- О роли открытия неевклидовой геометрии.
- Свойства аксиоматических систем.
- Понятие математической структуры.
- Модель или реализация системы аксиом.
- Формальная и содержательная аксиоматики. Теории и структуры.
- Другими словами, Изоморфизм моделей - это такое взаимно-однозначное соответствие между элементами моделей, которое сохраняет отношения элементов, задаваемые системой аксиом.
- Требования , предъявляемые к системам аксиом.
- Независимость аксиоматической системы.
- Независимость аксиомы параллельности.
- Определение (дедуктивной полноты).
- Историческая роль V постулата Евклида в развитии оснований математики.
- Анализ текстовых парадоксов. . Языковые свойства имен объектов. . Пример 1. . Пример 2. . Пример 3.
- Проблема выразимости.. Понятие искусственного языка.
- Парадокс достижимости в натуральном ряде.
1.2 Операции, определяющие формирование множества рациональных чисел.
Практическая необходимость перечислять предметы привела к формированию понятия натурального ряда. Практическая же необходимость арифметических операций над натуральными числами приводит к формированию более широкого класса величин - рациональным числам. Схематично это выглядит так:
Натуральный ряд N
L
Операция сложения “+”; операция вычитания " - " обратная к сложению
Множество Z целых чисел (положительные, отрицательные и ноль)
Множество Z
L
Операция умножения “х”; обратная операция “:” деление.
Множество Q рациональных чисел
вида 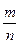
Схема 2
Вывод 1.
Множество чисел представимых в виде несократимых дробей m/n, где: m, n, N, n 0 называется множеством рациональных чисел и обозначается Q. На этом множестве определим операции ±, ´, :, и результат действия этих операций над рациональными числами есть снова рациональное число.
Мы не будем обсуждать все свойства рациональных чисел, а ограничимся напоминанием свойств систематического представления рациональных чисел, известных из элементарного курса математики.
Наличие операций сложения и умножения позволяет построить представление целых чисел при помощи алфавита, содержащего К знаков, называемых цифрами.
Такое представление дается записью вида:  a a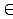 N N
a = anKn+... + a1K+ao (5)
и называется систематической К-ичной записью по основанию К. Символы ao, a1, ... , an принимают одно из К значений 0,1,2, ... , K-1. Если K 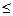 10, то для обозначения K цифр используют первые К цифр десятичной системы 0,1,2, ... , К-1. Для обозначения степеней оснований (классов) К1, К2, ..., Кn используются уже введенные числовые обозначения (классы “тиражируются медленнее”, чем числа, входящие в эти классы). 10, то для обозначения K цифр используют первые К цифр десятичной системы 0,1,2, ... , К-1. Для обозначения степеней оснований (классов) К1, К2, ..., Кn используются уже введенные числовые обозначения (классы “тиражируются медленнее”, чем числа, входящие в эти классы).
Запись целых чисел в K-ичной системе позволяет реализовать арифметические операции над рациональными числами в виде некоторых алгоритмов, то есть правил выполнения последовательности простых операций над цифрами, представляющими рациональные числа.
В школьном курсе изучаются алгоритмы арифметических операций в десятичной системе.
Напомним для примера алгоритм сложения целых чисел.
Пусть а = 247 = 2 . 102 +4 . 10+7, в = 378 = 3 . 102 + 7 . 10 + 8
Найти С = а+в.
Складывая цифры, нумерующие разряды единиц, десятков и сотен, получаем:
7+8 = 10+5 (единицы)
4 .10 + 7 . 10 = 102+10 (десятки)
2 . 102 + 3 . 102 = 5 . 102 (сотни)
Учитывая правила формирования разрядов, составляем десятичную запись числа С= а+в:
С = (102 +5 . 102) + (10+10)+5 = 6 . 102 +2 . 10+5 = 625
Кроме реализации арифметических операций, систематическое представление чисел дает алгоритм сравнения чисел по величине.
Для сравнения целых положительных чисел достаточно сравнить цифры разрядов по старшинству, например: 197<211, так как 197<2.102, а 211 > 2.102.
Алгоритм представления рационального числа 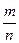 в десятичной записи приводит к двум типам записи, известным из школьного курса. в десятичной записи приводит к двум типам записи, известным из школьного курса.
Всякое рациональное число может быть представлено конечной десятичной дробью вида:
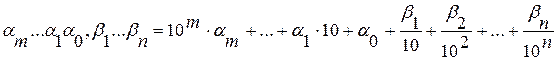 , (6) , (6)
либо бесконечной периодической дробью вида:
 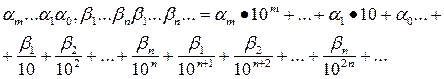 (7) (7)

Напомним так же, что алгоритм представления рационального числа в виде (6) или (7) основан на следующем свойстве целых чисел.
Для любых a, b 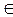 N , (a > b) существуют m, n N , (a > b) существуют m, n 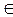 N,(m<a, n<b) такие, что N,(m<a, n<b) такие, что
а = bm+n (8)
|