

Мы поможем в написании ваших работ!
ЗНАЕТЕ ЛИ ВЫ?
|
Существуют числа, не являющиеся результатом конечного числа арифметических операций над целыми числами и не представимые в виде p/q ни для каких целых p, Q.
Содержание книги
- Сущность языковых систем состоит в том, что закономерности мыслительных процессов реализуются в законах организации текстовых структур.
- Каковы закономерности знаковых систем, представляющих интеллектуальную продукцию в текстовой форме?
- О понятии действительных чисел
- Операции, определяющие формирование множества рациональных чисел.
- Аксиоматика рациональных чисел должна содержать правила, определяющие операции сложения, умножения, сравнения чисел и связь между этими операциями.
- Аксиома связи сложения и умножения.
- Задачи, приводящие к расширению множества рациональных чисел.
- Существуют числа, не являющиеся результатом конечного числа арифметических операций над целыми числами и не представимые в виде p/q ни для каких целых p, Q.
- О представлении действительных чисел.
- Аксиоматическое обоснование евклидовой геометрии.
- Аксиоматика Д. Гильберта(1862-1943)
- Группа 3. Аксиомы конгруэнтности.
- Теорема (о внешнем угле треугольника).
- Группа 4. Аксиомы непрерывности.
- Группа 5. Аксиома параллельности.
- Два недостатка аксиоматики Д. Гильберта.
- Структура векторного пространства.
- Множество всех векторов назовем векторным пространством, а построенную модель направленных отрезков - геометрической моделью векторного пространства.
- Если в пространстве задан базис { 1, 2, 3}, то между множеством векторов и упорядоченными тройками чисел (x,y,z) установлено взаимно-однозначное соответствие
- Абстрактное векторное пространство.
- Определение абстрактного векторного пространства.
- Аксиомы скалярного произведения векторов.
- Модель Вейля евклидовой геометрии.
- Свойства операции откладывания вектора.
- Многомерное арифметическое евклидово пространство.
- Модель А. Пуанкаре плоскости Лобачевского.
- Определение плоскости Лобачевского.
- Основные факты в планиметрии Лобачевского.
- Взаимное расположение прямых в плоскости L2.
- О роли открытия неевклидовой геометрии.
- Свойства аксиоматических систем.
- Понятие математической структуры.
- Модель или реализация системы аксиом.
- Формальная и содержательная аксиоматики. Теории и структуры.
- Другими словами, Изоморфизм моделей - это такое взаимно-однозначное соответствие между элементами моделей, которое сохраняет отношения элементов, задаваемые системой аксиом.
- Требования , предъявляемые к системам аксиом.
- Независимость аксиоматической системы.
- Независимость аксиомы параллельности.
- Определение (дедуктивной полноты).
- Историческая роль V постулата Евклида в развитии оснований математики.
- Анализ текстовых парадоксов. . Языковые свойства имен объектов. . Пример 1. . Пример 2. . Пример 3.
- Проблема выразимости.. Понятие искусственного языка.
- Парадокс достижимости в натуральном ряде.
Вывод 3.
Существуют числа, не являющиеся результатом конечного числа арифметических операций над целыми числами и не представимые в виде p/q ни для каких целых p, q.
Числа, не представимые в виде p/q ни для каких целых p, q, называются иррациональными.
1.5 Аксиоматизация множества действительных чисел.

Конструктивное построение множества действительных чисел можно представить в виде схемы.
Непрерывными операциями мы называем вычислительные алгоритмы, состоящие из арифметических и других простых операций, пронумерованных натуральным рядом. Описание непрерывных операций потребует разработки вспомогательных понятий. Избежать такой дополнительной работы можно аксиоматическим заданием множества действительных чисел.
Добавим к аксиомам, определяющим в П. З. множество рациональных чисел Q, еще одну, следующую аксиому.
Аксиома непрерывности Кантора.
16. Пусть элементы x 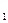 ,x ,x 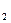 ,…,x ,…,x 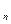 ,…,y ,…,y 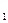 ,y ,y 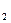 ,…,y ,…,y 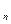 ,… удовлетворяют условию x ,… удовлетворяют условию x 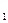 <x <x 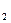 <…<x <…<x 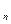 <…<y <…<y 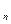 <…y <…y 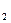 <y <y 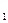 и пусть для любого положительного элемента e>0, начиная с некоторого номера n, выполняются условия y и пусть для любого положительного элемента e>0, начиная с некоторого номера n, выполняются условия y 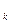 -x -x 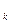 < e, k = n, n+1, … . Тогда существует элемент Z такой, что при всех значениях n выполняется x < e, k = n, n+1, … . Тогда существует элемент Z такой, что при всех значениях n выполняется x 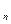 < Z < y < Z < y 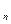 . .
То, что элемент Z, о котором говорится в этой аксиоме, является единственным, несложно доказать от противного.
|