

Мы поможем в написании ваших работ!
ЗНАЕТЕ ЛИ ВЫ?
|
Математической основой взаимного ориентирования пары снимков является условие компланарности трех векторов . Все три вектора лежат в
Математической основой взаимного ориентирования пары снимков является условие компланарности трех векторов . Все три вектора лежат в
1. плоскости левого снимка;
2. базисной плоскости;
3. главной базисной плоскости правого снимка;
4. главной базисной плоскости левого снимка;
5. плоскости правого снимка
Для нахождения ЭВ3О необходимо на снимках стереопары выбрать одноименные точки. Минимальное число точек равно
1. 3;
2. 4;
3. 5;
4. 6;
5. 9
Элементы взаимного ориентирования определяются по измеренным поперечным параллаксам q в точках ориентирования 1÷6, расположенных по стандартной схеме. Элемент ориентирования зависит от q в точках ориентирования
1. 1, 2;
2. 3, 5;
3. 4, 6;
4. 3, 4, 5, 6;
5. 1, 2, 3. 4, 5, 6
Элементы взаимного ориентирования определяются по измеренным поперечным параллаксам q в точках ориентирования 1÷6, расположенных по стандартной схеме. Элемент ориентирования зависит от q в точках ориентирования
1. 1, 2;
2. 3, 5;
3. 4, 6;
4. 3, 4, 5, 6;
5. 1, 2, 3. 4, 5, 6
Элементы взаимного ориентирования определяются по измеренным попе-речным параллаксам q в точках ори-ентирования 1÷6, расположенных по стандартной схеме. Элемент ориенти-рования зависит от q в точках ориен-тирования
1. 1, 2;
2. 3, 5;
3. 4, 6;
4. 3, 4, 5, 6;
5. 1, 2, 3. 4, 5, 6
Элементы взаимного ориентирова-ния пары плановых снимков расчи-тываются по формулам связи с попе-речными параллаксами в точках ори-ентирования 1÷6. Элемент ориенти-рования вычисляют по формуле
1. 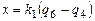 ; ;
2. 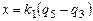 ; ;
3. 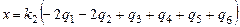 ; ;
4. 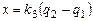 ; ;
5. 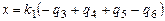 , ,
где 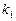 - коэффициенты. - коэффициенты.
|