Для определения элементов внеш-него ориентирования модели необ-ходимо иметь

Для плановых снимков стереопары поперечные параллаксы q в точках ориентирования 1÷6 измеряются на стереокомпораторе. Контроль результатов измерений q в точках ориентирования 1÷6 осуществляется по величине невязки W, рассчитанной по формуле

1. ;

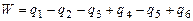2. ;

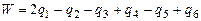3. ;

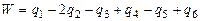4. ;

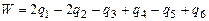5.

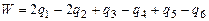
При аналитическом способе опреде-ления ЭВ3О исходным уравнением является уравнение компланарности, приведенное к линейному виду. В это уравнение входят поправки к опреде-ляемым величинам, число которых равно

1. 3;

2. 4;

3. 5;

4. 6;

5. 9

Задача определения ЭВ3О аналитическим способом решается последовательными приближениями по методу наименьших квадратов. На основе системы уравнений поправок, составленных для точек ориентирования 1÷6 образуется система нормальных уравнений, включающая

1. 3 уравнения;

2. 4 уравнения;

3. 5 уравнений;

4. 6 уравнений;

5. 9 уравнений

Модель местности строится путем взаимного ориентирования снимков стереопары в произвольном масштабе и ее ориентирования в принятой системе координат местности. Для ее масштабирования и ее ориентирования необходимо знать элементы внешнего ориентирования, число которых равно

1. 3;

2. 4;

3. 5;

4. 7;

5. 9

1. геодезические координаты опорных точек и плоские координаты их изображений на снимках стереопары;

2. пространственные X, Y, Z и плоские x, y, z координаты соответственных точек снимков;

3. геодезические координаты опорных точек и пространственные 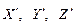 координаты их изображений на снимках;

4. геодезические и пространственные фотограмметри-ческие координаты опорных точек;

5. элементы внешнего ориентирования