Математической основой для определения эв3о снимков стереопары является уравнение компланарности. Для первой системы эв3о это уравнение в координатной форме имеет вид
Математической основой для определения ЭВ3О снимков стереопары является уравнение компланарности. Для первой системы ЭВ3О это уравнение в координатной форме имеет вид
1. 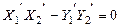 ; ;
2. 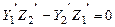 ; ;
3. 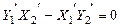 ; ;
4. 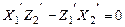 ; ;
5. 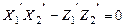
В уравнении взаимного ориентиро-вания (I система) ордината зави-сит от
1. 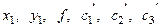 ; ;
2. 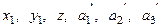 ; ;
3. 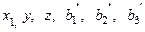 ; ;
4. 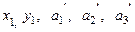 ; ;
5. 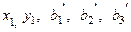
В уравнении взаимного ориентиро-вания (I система) ордината зави-сит от
1. 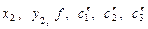 ; ;
2. 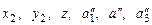 ; ;
3. 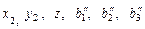 ; ;
4. 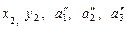 ; ;
5. 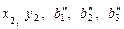
ЭВ3О используется для построения модели объекта на аналоговых приборах. Модель создается путем устранения поперечных параллаксов в точках ориентирования путем угловых поворотов и линейных перемещений камер прибора. При использовании первой системы ЭВ3О поперечный параллакс в точке 2 устраняется движением
6. 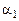 ; ;
7. 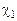 ; ;
8. 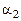 ; ;
9. 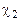 ; ;
10. 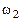
ЭВ3О используется для построения модели объекта на аналоговых приборах. Модель создается путем устранения поперечных параллаксов в точках ориентирования путем угловых поворотов и линейных перемещений камер прибора. При использовании второй системы ЭВ3О поперечный параллакс в точке 1 устраняется движением
1. 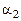 ; ;
2. 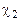 ; ;
3. 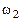 ; ;
4. 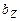 ; ;
5. 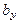
ЭВ3О используется для построения модели объекта на аналоговых приборах. Модель создается путем устранения поперечных параллаксов в точках ориентирования путем угловых поворотов и линейных перемещений камер прибора. При использовании второй системы ЭВ3О поперечный параллакс в точке 3 устраняется движением
1. 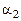 ; ;
2. 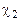 ; ;
3. 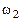 ; ;
4. 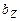 ; ;
5. 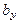
ЭВ3О используется для построения модели объекта на аналоговых приборах. Модель создается путем устранения поперечных параллаксов в точках ориентирования путем угловых поворотов и линейных перемещений камер прибора. При использовании второй системы ЭВ3О поперечный параллакс в точке 4 устраняется движением
1. 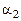 ; ;
2. 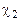 ; ;
3. 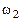 ; ;
4. 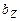 ; ;
5. 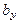
|