
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Несобственный интеграл второго родаСодержание книги
Поиск на нашем сайте
Пусть функция
В частности, если существует первообразная
Пример.Вычислим – Следовательно, рассматриваемый интеграл сходится и равен –1. Если же особой точкой функции Если особая точка
ЛИТЕРАТУРА
1. Данко, П.Е. Высшая математика в упражнениях и задачах. Т.1, Т.2/ П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова. – М.: Высшая школа, 2003.– 460с. 2. Матвеев, Н.М. Методы интегрирования обыкновенных дифференциальных уравнений: учебное пособие/ Н.М.Матвеев. – СПб.: Издательство «Лань», 2003.–832с. 3. Пискунов, Н.С. Дифференциальное и интегральное исчисления: учеб. пособие для вузов. В 2 т.Т.1. и Т.2./ Н.С. Пискунов. – М.: Интеграл-Пресс, 2002.- 415 с. и 544с. 4. Фихтенгольц, Г.М. Курс дифференциального и интегрального исчисления: учебник в 3-х т. / Г. М. Фихтенгольц. - 9-е изд., стер. – СПб.; М.; Краснодар: Лань, 2009.–608,800, 672с.
ОГЛАВЛЕНИЕ
Введение 3 Задания к контрольной работе 1 4 Методические указания к контрольной работе 1 11 Определители 13 1. Определитель второго порядка 14 2. Определитель третьего порядка 14
3. Определители более высокого порядка 15 Обратная матрица 15 Решение линейных систем с помощью обратной матрицы 18 Таблица производных основных элементарных функций 36 Производные более высокого порядка 38 Дифференциал и его свойства 40 Задания контрольной работы 2 41 Методические указания к контрольной работе 2 47 Экстремум функции двух переменных 62 Таблица неопределенных интегралов 65 Свойства определенного интеграла 69 Методы интегрирования 70 Список литературы 75
|
|||||
|
Последнее изменение этой страницы: 2024-06-27; просмотров: 9; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.239.215 (0.006 с.) |

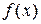 интегрируема на любом конечном промежутке
интегрируема на любом конечном промежутке 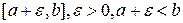 , а точка
, а точка 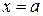 является особой точкой функции
является особой точкой функции 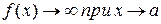 ). Тогда несобственным интегралом от функции
). Тогда несобственным интегралом от функции 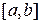 называют
называют 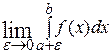 и обозначают так же, как и определённый интеграл
и обозначают так же, как и определённый интеграл 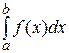 . Если указанный предел существует, то несобственный интеграл сходится, в противном случае говорят, что несобственный интеграл расходится.
. Если указанный предел существует, то несобственный интеграл сходится, в противном случае говорят, что несобственный интеграл расходится.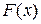 функции
функции 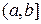 , тогда
, тогда 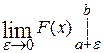 =
= 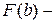
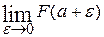 = =
= = 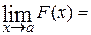
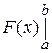 , где подстановка в точке
, где подстановка в точке 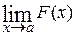 .
. . Так как
. Так как 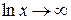 при
при 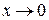 , то рассматриваемый интеграл является несобственным интегралом второго рода и, по определению,
, то рассматриваемый интеграл является несобственным интегралом второго рода и, по определению, 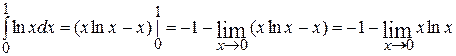 = (применим правило Лопиталя) =
= (применим правило Лопиталя) = 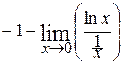 =
= 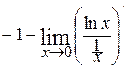 =
= 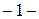
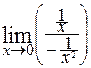 =
= 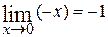 .
.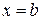 , тогда
, тогда 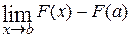 . Например,
. Например, 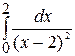 =
= 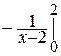 = =
= = 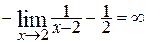 и этот интеграл расходится.
и этот интеграл расходится.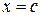 лежит внутри промежутка интегрирования
лежит внутри промежутка интегрирования 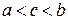 , тогда, по определению, несобственный интеграл
, тогда, по определению, несобственный интеграл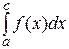 +
+ 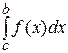 .
.


