
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойства определённого интегралаСодержание книги
Поиск на нашем сайте
Свойства определённого интеграла 1. Если функция 2. Если функция 3. Линейность определённого интеграла. Для любых постоянных справедливо равенство 4. Аддитивность. Если 5.
Формула Ньютона–Лейбница.Если функция
Методы интегрирования 1. Формула интегрирования по частям для определённого интеграла. Пусть функции
Равенство (12) называют формулой интегрирования по частям. Рассмотрим некоторые примеры вычисления определённых интегралов при помощи этой формулы. Основные типы интегралов, которые вычисляются только с помощью интегрирования по частям, уже были рассмотрены в примерах к предыдущему заданию. В этом пункте рассмотрим дополнительно ещё несколько интегралов такого вида. Пример.Вычислим – Следовательно, получили уравнение относительно исходного интеграла Пример.Вычислим с помощью формулы интегрирования по частям =
2. Замена переменной в определённом интеграле. Пусть функция
Пример.Вычислим интеграл
|
||||
|
Последнее изменение этой страницы: 2024-06-27; просмотров: 5; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.167.11 (0.007 с.) |

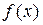 непрерывна на промежутке
непрерывна на промежутке 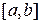 , тогда
, тогда 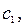
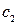
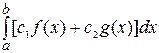 =
= 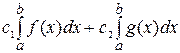 .
.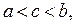 тогда
тогда 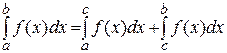 .
.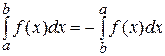 . 6). Если
. 6). Если 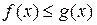 на промежутке
на промежутке 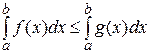 (функциональные неравенства можно интегрировать).
(функциональные неравенства можно интегрировать).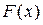 и выполняется равенство
и выполняется равенство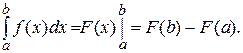
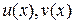 – непрерывно дифференцируемые функции на промежутке
– непрерывно дифференцируемые функции на промежутке 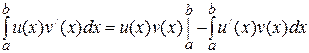 . (12)
. (12)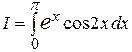 . Применив формулу (11), получим
. Применив формулу (11), получим 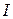 =
= 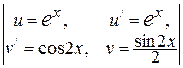 =
= 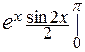 –
– 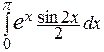 = –
= – 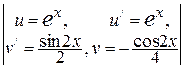 =
= 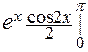 –
–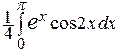 =
= 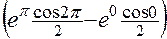 –
– 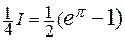 –
– 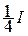 .
.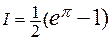 –
– 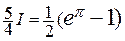 или
или 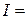 =
= 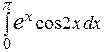 =
= 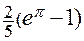 .
.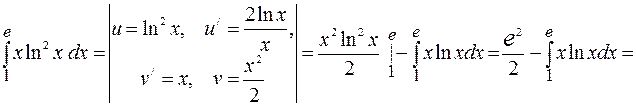 (применим ещё раз формулу интегрирования по частям)
(применим ещё раз формулу интегрирования по частям) 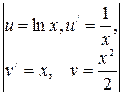 =
=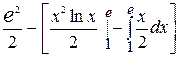 =
= 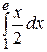 =
= 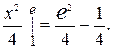
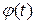 непрерывно дифференцируема на промежутке
непрерывно дифференцируема на промежутке 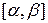 и
и 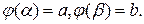 Тогда справедливо равенство
Тогда справедливо равенство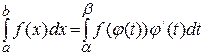 . (13)
. (13)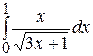 с помощью формулы (13). Сделаем в этом интеграле замену переменной
с помощью формулы (13). Сделаем в этом интеграле замену переменной 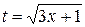 , тогда
, тогда 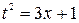 ,
, 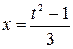 . Продифференцировав последнее равенство, получим
. Продифференцировав последнее равенство, получим 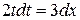 или
или 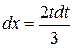 . Пределы интегрирования по новой переменной
. Пределы интегрирования по новой переменной 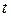 находим из формулы замены
находим из формулы замены 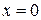 , а затем верхний предел интегрирования
, а затем верхний предел интегрирования 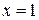 . После этой замены получаем
. После этой замены получаем 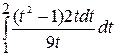 =
= 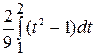 =
= 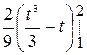 = =
= = 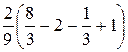 =
= 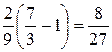 .
.


