
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Диэлектрическая восприимчивость.Содержание книги Поиск на нашем сайте
Рассмотрим неполярный диэлектрик, помещённый во внешнее электрическое поле с напряженностью
Неполярные молекулы во внешнем электрическом поле поляризуются: молекула диэлектрика приобретает индуцированный (наведенный) дипольный момент Состояние диэлектрика во внешнем электрическом поле характеризуют вектором
Если в однородном неполярном диэлектрике с концентрацией молекул n все молекулы одинаковы, то и поляризуются в электрическом поле они одинаково. В этом случае используя в (2) значение (1) для
где Молекулы полярных диэлектриков обладают электрическим моментом и в отсутствии электрического поля, причём их момент на порядок больше момента
В твердых диэлектриках, имеющих ионную кристаллическую решетку, внешнее электрическое поле вызывает смещение всех положительных ионов в направлении вектора напряженности
§11. Теорема Гаусса для электростатического поля в диэлектрике.Диэлектрическая проницаемость. Вектор D
Электрическое поле в диэлектрике создается как свободными, так и связанными зарядами и теорема Гаусса для электростатического поля в диэлектрике должна отличаться от теоремы Гаусса в вакууме только тем что в (5.6)-(5.7) под зарядом q следует понимать сумму свободных и связанных зарядов (q + q ´) внутри замкнутой поверхности:
Связанные заряды Приведём без вывода основные соотношения, возникающие при анализе формулы (1). С использованием величин, рассмотренных в §10, вводятся следующие соотношения. Величину
называют электрическим смещением, а уравнение
называют теоремой Гаусса для электростатического поля в среде. Для электронной и дипольной поляризации однородного изотропного диэлектрика справедливо соотношение (10.3) и выражение (3) существенно упрощается:
где величину ε
называют диэлектрической проницаемостью среды. Величина ε среды достаточно просто определяется экспериментально по измерениям электроёмкости конденсатора с диэлектриком и без него и приведена для большинства диэлектриков в справочниках. С учётом (5) теорему Гаусса (4) для электростатического поля в среде можно записать в виде
2. Напряженность поля, образованного заряженным шаром
где 3. Напряженность поля равномерно заряженной бесконечно длинной нити (цилиндра)
где
§13 Проводники в электростатическом поле
В проводниках есть свободные заряды, способные перемещаться в пределах проводника в сколь угодно слабом электрическом поле. Если проводник зарядить или просто поместить во внешнее электростатическое поле Отсутствие поля внутри проводника (
Решение задач
ЗАДАЧА 5. 5. Вычислить поля вблизи поверхности проводника (в отсутствии и в присутствии диэлектрика). Вычислить плотность связанных зарядо σ´ на поверхности диэлектрика, прилегющей к поверхности проводника.
и
Тогда и Для электростатического поля вблизи поверхности проводника, окружённого однородным изотропным диэлектриком (рис.13.2) из(6) . (13.1) Выберем поверхность интегрирования в виде малого прямого цилиндра с площадью оснований S 01= S 02. Заряд q, заключённый внутри объёма цилиндра равен q = σ S 01, а интеграл в (7) равен Е ∙ S 01. Приравнивая, получим В отсутствии диэлектрика
Уменьшение поля (8) происходит за счет поля, создаваемого связанным зарядом σ´ на поверхности диэлектрика. .
Теоретическое введение §14. Электроемкость Конденсатор представляет собой систему двух проводников (обкладок), разделенных диэлектриком. Если сообщить обкладкам равные по величине и противоположные по знаку заряды q и - q, то разность потенциалов между обкладками будет пропорциональна величине q j1 - j2 = где С - емкость конденсатора: величина, численно равная отношению заряда одной обкладки к разности потенциалов между обкладками
С = Ёмкость конденсатора зависит от геометрических характеристик обкладок конденсатора, их взаимного расположения и диэлектрических свойств среды между ними. Емкость плоского конденсатора, состоящего из двух обкладок С =
При параллельном соединении (рис. 14.1) заряды равны
Общий заряд батареи равен сумме зарядов всех конденсаторов
Полная емкость батареи
Разность потенциалов на зажимах батареи равна сумме разностей потенциалов на обкладках каждого из конденсаторов
где При последовательном соединении конденсаторов суммируются величины, обратные емкостям входящих в батарею конденсаторов.
При таком соединении электрическая емкость
|
|||||||||||||||
|
Последнее изменение этой страницы: 2022-09-03; просмотров: 138; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.174.253 (0.011 с.) |
||||||||||||||||

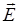 . Под действием сил поля происходит поляризация диэлектрика: смещение центров распределения положительных (ядер) и отрицательных (электронных оболочек) зарядов молекул в противоположные стороны на величину
. Под действием сил поля происходит поляризация диэлектрика: смещение центров распределения положительных (ядер) и отрицательных (электронных оболочек) зарядов молекул в противоположные стороны на величину 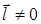 относительно друг друга. В результате молекулы приобретают электрический момент
относительно друг друга. В результате молекулы приобретают электрический момент  , направленный вдоль поля. Для неполярных молекул выполняется равенство
, направленный вдоль поля. Для неполярных молекул выполняется равенство . (1)
. (1)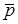 , пропорциональный напряженности внешнего поля. Коэффициент α зависит только от объема молекулы и называется поляризуемостью. Отметим, что в поле
, пропорциональный напряженности внешнего поля. Коэффициент α зависит только от объема молекулы и называется поляризуемостью. Отметим, что в поле 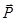 , называемом поляризованностью и равному суммарному электрическому моменту всех молекул в единице объёма диэлектрика:
, называемом поляризованностью и равному суммарному электрическому моменту всех молекул в единице объёма диэлектрика: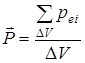 . (2)
. (2) можно записать
можно записать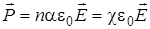 :
: , (3)
, (3)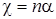 - безразмерная величина, называемая диэлектрической восприимчивостью диэлектрика.
- безразмерная величина, называемая диэлектрической восприимчивостью диэлектрика.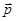 (1), приобретаемого молекулами неполярного диэлектрика в электрическом поле. Однако, тепловое движение молекул приводит к хаотичному разбросу направлений их электрических моментов и в отсутствии электрического поля поляризованность диэлектрика (2) равна нулю. Под действием поля возникает преимущественная ориентация электрических моментов молекул вдоль поля (дипольная или ориентационная поляризация), возрастающая с увеличением напряженности
(1), приобретаемого молекулами неполярного диэлектрика в электрическом поле. Однако, тепловое движение молекул приводит к хаотичному разбросу направлений их электрических моментов и в отсутствии электрического поля поляризованность диэлектрика (2) равна нулю. Под действием поля возникает преимущественная ориентация электрических моментов молекул вдоль поля (дипольная или ориентационная поляризация), возрастающая с увеличением напряженности  и с уменьшением температуры и в не слишком сильных полях справедливо соотношение (3).
и с уменьшением температуры и в не слишком сильных полях справедливо соотношение (3). . (1)
. (1)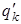 возникают в результате поляризации диэлектрика и их величина должна быть связана с его поляризованностью
возникают в результате поляризации диэлектрика и их величина должна быть связана с его поляризованностью 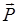 .
.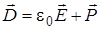 (3)
(3)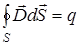 , (4)
, (4) , т.е.
, т.е.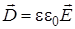 , (5)
, (5)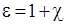 (6)
(6)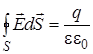 . (7)
. (7)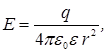 (1.28)
(1.28)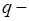 заряд шара радиуса
заряд шара радиуса 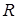 ;
; 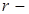 расстояние от центра шара до точки поля (
расстояние от центра шара до точки поля (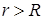 ).
).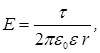 (1.29)
(1.29) линейная плотность заряда на нити (заряд, приходящийся на единицу длины);
линейная плотность заряда на нити (заряд, приходящийся на единицу длины);  , имеющее противоположное
, имеющее противоположное 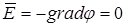 ) означает, что потенциал во всех точках внутри проводника постоянен, т.е. поверхность проводника в электростатическом поле является эквипотенциальной. Отсюда же вытекает, что вектор
) означает, что потенциал во всех точках внутри проводника постоянен, т.е. поверхность проводника в электростатическом поле является эквипотенциальной. Отсюда же вытекает, что вектор 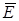 поля направлен по нормали к каждой точке поверхности проводника.
поля направлен по нормали к каждой точке поверхности проводника.

 РЕШЕНИЕ. Применим теорему Гаусса в присутствии диэлектрика (См формулы выше)
РЕШЕНИЕ. Применим теорему Гаусса в присутствии диэлектрика (См формулы выше)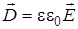 , (5)
, (5) (6)
(6) (7)
(7) . (8)
. (8) . (9)
. (9)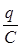 , (14.3)
, (14.3)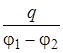 . (14.4)
. (14.4) . (14.7)
. (14.7)
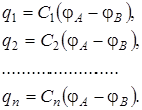

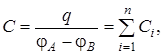 (14.8)
(14.8)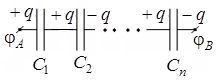
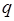 батареи.
батареи.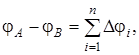
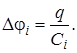

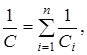 (14.9)
(14.9) батареи всегда меньше наименьшей емкости конденсатора, используемого в батарее.
батареи всегда меньше наименьшей емкости конденсатора, используемого в батарее.


