
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задача 1 (см. Теоретическое введение 1 стр. 13-17 )Содержание книги
Поиск на нашем сайте
ЗАДАЧА 1 (См. теоретическое введение 1 стр. 13-17)
ЗАДАЧА 2 (См. теоретическое введение 1 стр. 13-17)
ЗАДАЧА 3 (См. теоретическое введение 2 стр. 20-22) 3. Кольцо радиусом R = равномерно заряжено с линейной плотностью t Определить потенциал j точки, лежащей на перпендикуляре к плоскости кольца, восставленном из центра кольца, отстоящей на расстоянии h от его центра.
По теореме Пифагора
а потенциал, создаваемый всеми зарядами d q кольца L в т. А на перпендикуляре по (4.11) (4.12а), равен
где все величины в интеграле постоянные (кроме d q) и их можно вынести за знак интеграла
Интеграл
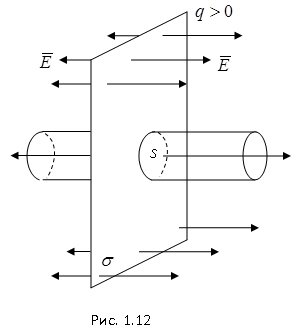
ЗАДАЧА 4 (См. теоретическое введение 3 стр. 23-25) . 4. Вычислить поле Е равномерно заряженной плоскости с поверхностной плотностью заряда s.
одинакова в любом месте плоскости. Это означает, что линии напряженности перпендикулярны плоскости в любой точке, т.е. поле заряженной плоскости однородно (рис. 1.12). Мысленно выделим в пространстве цилиндр, ось которого перпендикулярна плоскости и одно из оснований проходит через интересующую нас точку. Согласно теореме Гаусса,
С другой стороны, так как линии напряженности пересекают только основания цилиндра, поток вектора
Тогда
откуда
Приведем (без вывода) выражения для расчета напряженности электростатического поля, создаваемого разноименно заряженными параллельными бесконечно протяженными плоскостями (поле плоского конденсатора)
ЗАДАЧА 6 (См. теоретическое введение 5 стр. 32-35) .
ЗАДАЧА 7 (См. теоретическое введение 5 стр. 32-35)
ЗАДАЧА 8 (См. теоретическое введение 5 стр. 32-35)
ЗАДАЧА 9 (См. теоретическое введение 6 стр. 37-40)
ЗАДАЧА 10 (См. теоретическое введение 6 стр. 37-40)
РЕШЕНИЕ
ЗАДАЧА 11 (См. теоретическое введение 6 стр. 37-40)
ЗАДАЧА 12 (См. теоретическое введение 7 стр. 42-45)
ЗАДАЧА 13 (теоретическое введение См. стр.)
Теоретическое введение 1 §1. Закон Кулона. Принцип суперпозиции. Точечным зарядом называется заряженное тело, размерами и формой которого можно пренебречь в условиях рассматриваемой задачи. Взаимодействие в вакууме (рис.1) двух неподвижных точечных зарядов q и Q называется электростатическим и описывается законом Кулона
где r - расстояние между частицами с зарядами q и Q, находящимися в вакууме, Сила взаимодействия между точечными электрическими зарядами, находящимися в какой-либо среде, уменьшается и с учётом этого (1.2) принимает вид
где
Для электромагнитного взаимодействия справедлив принцип суперпозиции: сила, действующая на точечный заряд со стороны системы точечных зарядов, равна векторной сумме сил действующих на него со стороны каждого из зарядов по отдельности. Использование закона Кулона и принципа суперпозиции позволяет в принципе рассчитать электростатическое взаимодействие любых произвольно заряженных объектов.
§2. Напряженность электрического поля в вакууме. Напряженности поля.
Взаимодействие между зарядами осуществляется через электромагнитное поле, которое создается самими зарядами. Поле проявляет себя в том, что помещенный в него заряд испытывает действие силы. Опыт показывает, в вакууме сила, действующая на заряд, пропорциональна величине заряда
где коэффициент Из (2.1) следует способ определения величины напряженности
Если выбрать пробный заряд единичным q =+1, то вектор Электростатика изучает поля, создаваемые неподвижными заряженными телами. Такое электромагнитное поле называют электростатическим. Его характеристики не изменяются со временем т.е.
Единицей измерения напряженности поля в СИ служит 1 Н/Кл =1 В/м. Если записать силу, действующей на точечный заряд q, в виде (1.3) и в виде (2.3) и приравнять выражения, то получим
где Модуль вектора напряженности поля точечного заряда Q на расстоянии r от него E = Вектор напряженности данного поля в любой точке направлен вдоль прямой, соединяющей эту точку и заряд (рис.2.1).
Для напряженности поля, так же как и для сил, справедлив принцип суперпозиции: напряженность поля, создаваемого любым числом точечных зарядов, равна векторной сумме напряженностей полей, создаваемых в рассматриваемой точке пространства каждым зарядом в отдельности
§3. Применение принципа суперпозиции для расчёта полей.
Формулы (2.4) и (2.6) позволяют в принципе рассчитать напряженность электрического поля любой системы зарядов Q 1... Qn, если известны их положения Непрерывное распределение зарядов по объему V заряженного тела, полный заряд которого q, характеризуют объемной плотностью заряда r = dq =r dV и Если тело заряжено по объему V равномерно, то r = const и полный заряд тела q = r V. При непрерывном распределении заряда по поверхности S тела рассматривается поверхностная плотность заряда s = dq =s dS и Если тело заряжено по поверхности равномерно то s = const и полный заряд тела q = s S. Непрерывное распределение зарядов вдоль тонкого стержня (“линии, нити”) характеризует линейная плотность заряда t = dq =t dl и В случае непрерывного распределения зарядов заряженное тело мысленно разбивается на малые части (dV , dS или dl) с зарядами dq, поле каждого из которых рассматривается как поле точечного заряда. Сложение напряженностей поля (рис.3.1) таких зарядов сводится к интегралам вида
.
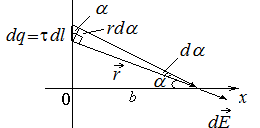
Рис.3.1. В частности, для величины напряженности поля равномерно заряженной бесконечной прямолинейной нити получается выражение
напряженность электрического поля равномерно заряженной бесконечной плоскости -
где s - поверхностная плотность заряда,
Для наглядного изображения поля используют силовые линии. Силовая линия электрического поля - линия, касательная к которой в каждой точке поля совпадает с напряженностью
Решение задач
ЗАДАЧА 1
ЗАДАЧА 2
Теоретическое введение 2
§4. Работа в электростатическом поле. Разность потенциалов. Потенциал электрического поля. Связь потенциала с напряжённостью поля. Принцип суперпозиции для потенциала. Электростатические силы являются потенциальными - их работа А 12по перемещению частицы с зарядом q из точки 1 в точку 2 не зависит от формы траектории, определяется только начальным и конечным положением частицы и пропорциональна величине q перемещаемого заряда.
Работа, совершаемая при перемещении электрического заряда во внешнем электростатическом поле по любому замкнутому (отражено кружком на значке интеграла) пути L равна нулю, т.е.
где dA =
Силовое поле E, циркуляция которого равна нулю, является в силу (4.2) также потенциальным. Величина работы A 12 сил поля, равная по (4.1)
A 12 = q (j1 - j2), (4.4) равна, с другой стороны, убыли потенциальной энергии частицы в потенциальном поле сил А 12 = -Δ W n= W n1 - W n2. (4.5) Из (4.4) и (4.5) следует связь потенциала с потенциальной энергией Wn заряда q в этой точке
Введенное понятие разности потенциалов (4.1) и связь (4.6) потенциала j с потенциальной энергией Wn не дают однозначного определения j, так как добавление к j любой постоянной величины не изменяет разности потенциалов (и работы), а Wn принципиально задана с точностью до некоторой постоянной. Разность же потенциалов (4.1) определена однозначно, так как при вычитании постоянная сокращается. Если выбрать точку и задать в ней значение j, то после этого потенциал в любой другой точке поля будет иметь определенное значение. Для заряженных тел, занимающих ограниченный объем, удобно считать потенциал равным нулю на бесконечном удалении от зарядов. Единицей измерения потенциала (и разности потенциалов) является 1 вольт (1 В = 1 Дж/Кл). Работа по перемещению точечного положительного заряда q из одной точки поля в другую вдоль оси х на элементарное расстояние
Рис.4.1 где В математике вектор, показывающий направление наибольшего роста скалярной функции П, называется градиентом (обозначается
т.е. напряженность поля равна градиенту потенциала со знаком «минус». Это означает, что вектор напряженности электростатического поля направлен в сторону убывания потенциала. Геометрическое место точек с одинаковым потенциалом называется эквипотенциальной поверхностью. Силовые линии перпендикулярны эквипотенциальным поверхностям и направлены в сторону уменьшения потенциала. При перемещении d х по эквипотенциальной поверхности d j = 0 и по (4.8) Ех = 0, т.е. вектор В этом случае где U = j1 - j2, d - расстояние между эквипотенциальными поверхностями с потенциалами j1 и j2. Напряженность
По напряжённости поля точечного заряда Q и (4.7) находим потенциал на расстоянии r от заряда
при этом считаем, что j ® 0 при r ® ¥. Для потенциала справедлив принцип суперпозиции: потенциал поля, создаваемого любым числом точечных зарядов, равен сумме потенциалов полей, создаваемых в рассматриваемой точке пространства каждым зарядом в отдельности
Формулы (4.11) и (4.12) позволяют в принципе рассчитать потенциал поля любой системы зарядов, занимающей ограниченный объем:
Рассуждения, поясняющие метод вычислений, совершенно аналогичны приведенным в § 2, следует лишь заменить в них величину вектор Е на скаляр j. Связь напряженности и потенциала (4.7) - (4.9) используется в ряде случаев для расчета потенциала. В частности, вычисление потенциала поля заряженной с поверхностной плотностью s бесконечной плоскости на расстоянии х от нее даёт
Если положить j = 0 при х = 0, то const = 0. На практике сначала вычисляют потенциал j, а затем по (4.7) находят проекции поля на оси выбранной системы координат. Решение задач ЗАДАЧА 3 3. Кольцо радиусом R = равномерно заряжено с линейной плотностью t Определить потенциал j точки, лежащей на перпендикуляре к плоскости кольца, восставленном из центра кольца, отстоящей на расстоянии h от его центра.
По теореме Пифагора
а потенциал, создаваемый всеми зарядами d q кольца L в т. А на перпендикуляре по (4.11) (4.12а), равен
где все величины в интеграле постоянные (кроме d q) и их можно вынести за знак интеграла
Интеграл
Теоретическое введение 3 §5. Поток вектора напряжённости. Теорема Гаусса для электростатического поля в вакууме.
Выделим на поверхности S малый элемент dS (рис. 5.1). Пусть n - единичный вектор нормали к dS, a j угол между векторами Е и n. При вычислении некоторых поверхностных интегралов оказывается удобным представить дифференциал поверхности в векторной форме. По определению, вектором элемента площади
Также по определению, потоком вектора Е Рис. 5.1 через поверхность S называется поверхностный интеграл
В случае замкнутой поверхности (рис. 5.1) поток (5.2)
В качестве нормали выбирается внешняя нормаль к поверхности. Пусть точечный заряд q окружен произвольной замкнутой поверхностью S. Напряжённость электростатического поля Е в любой точке поверхности направлена вдоль радиус-вектора данной точки и вычисляется в соответствии с законом Кулона (2.4). В пределах малой площадки dS напряжённость электростатического поля можно считать постоянной. Вычислим поток (3) вектора Е через замкнутую поверхность.
В случае, когда поверхность S сферическая с центром в точке нахождения заряда q, вектора
Результат вычисления потока (5.3) вектора Е через произвольную замкнутую поверхность также оказывается равным (5.5), т.е.
Кроме того, если внутри поверхности находятся несколько точечных зарядов, то в правой части (5.6) под q следует понимать алгебраическую сумму зарядов внутри поверхности
Если внутри поверхности находится заряд, распределённый по объёму с плотностью r, то суммарный заряд, внутри поверхности равен
Уравнения (5.6) - (5.8) представляют собой выражения теоремы Гаусса для электростатического поля в вакууме: поток вектора напряжённости электростатического поля в вакууме сквозь произвольную замкнутую поверхность равен отношению алгебраической суммы зарядов внутри поверхности к электрической постояннойe 0. Теорема Гаусса может быть использована для вычисления напряжённости электростатического поля. Однако используется она в основном для случаев симметричного распределения зарядов, когда вычисление интегралов в правой части (5.6) - (5.8) достаточно простое. Из уравнения (5.8) можно получить дифференциальное уравнение, которому удовлетворяет поле Е
Уравнение (5.9), в отличие от уравнений (5.6) - (5.8), позволяет вычислить поле любой системы зарядов.
Решение задач ЗАДАЧА 4. 4. Вычислить поле Е равномерно заряженной плоскости с поверхностной плотностью заряда s.
одинакова в любом месте плоскости. Это означает, что линии напряженности перпендикулярны плоскости в любой точке, т.е. поле заряженной плоскости однородно (рис. 1.12). Мысленно выделим в пространстве цилиндр, ось которого перпендикулярна плоскости и одно из оснований проходит через интересующую нас точку. Согласно теореме Гаусса,
С другой стороны, так как линии напряженности пересекают только основания цилиндра, поток вектора
Тогда
откуда
Приведем (без вывода) выражения для расчета напряженности электростатического поля, создаваемого разноименно заряженными параллельными бесконечно протяженными плоскостями (поле плоского конденсатора)
Теоретическое введение 4
В состав молекул вещества входят заряженные частицы, но в целом они нейтральны. Молекула, в которой «центр тяжести» отрицательных зарядов (электронов) совпадает с «центром тяжести» положительных зарядов (протонов в атомных ядрах), называется неполярной. Если «центры тяжести» не совпадают - молекула называется полярной. Полярная молекула является примером электрического диполя. По определению, электрическим диполем называется система, состоящая из двух точечных электрических зарядов q +> 0 и q −< 0, расстояние l между которыми мало по сравнению с расстояниями r от этой системы до рассматриваемых точек пространства (рис. 7.1). Плечом диполя называется вектор l, направленный от отрицательного заряда к положительному, равный по модуля расстоянию между зарядами. Электрическим моментом диполя
Очевидно, при наличии поля электрический момент возникнет и у неполярных молекул, а у полярных он увеличится.
§6. Проводники и диэлектрики.
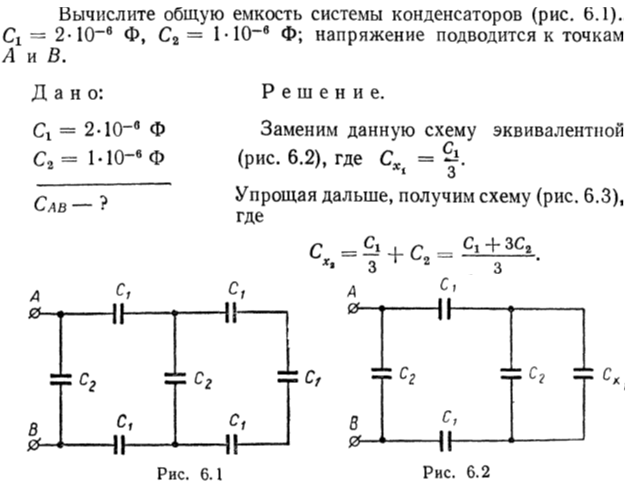
Все вещества по способности проводить электрический ток подразделяют на проводники и диэлектрики. Удельное сопротивление ρ Д диэлектриков на много порядков больше чем ρ П проводников: ρ Д~ §10. Диэлектрики в электрическом поле. Теоретическое введение §14. Электроемкость Конденсатор представляет собой систему двух проводников (обкладок), разделенных диэлектриком. Если сообщить обкладкам равные по величине и противоположные по знаку заряды q и - q, то разность потенциалов между обкладками будет пропорциональна величине q j1 - j2 = где С - емкость конденсатора: величина, численно равная отношению заряда одной обкладки к разности потенциалов между обкладками С = Ёмкость конденсатора зависит от геометрических характеристик обкладок конденсатора, их взаимного расположения и диэлектрических свойств среды между ними. Емкость плоского конденсатора, состоящего из двух обкладок С =
При параллельном соединении (рис. 14.1) заряды равны
Общий заряд батареи равен сумме зарядов всех конденсаторов
Полная емкость батареи
Разность потенциалов на зажимах батареи равна сумме разностей потенциалов на обкладках каждого из конденсаторов
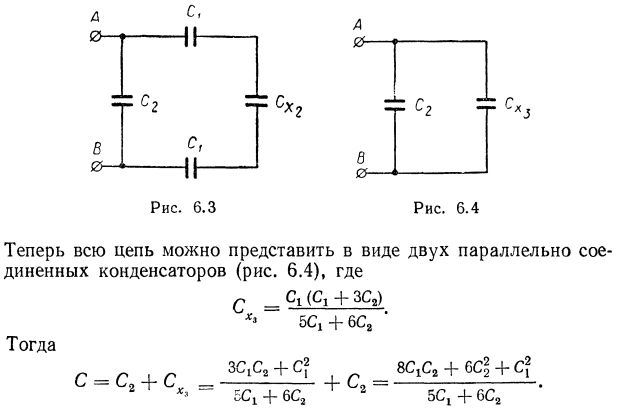
где При последовательном соединении конденсаторов суммируются величины, обратные емкостям входящих в батарею конденсаторов.
При таком соединении электрическая емкость И электростатического поля Соответственно, энергия заряженного конденсатора равна
Энергия однородного электростатического поля плоского конденсатора связана с напряженностью поля Е и объемом
Из (15.8) следует выражение для объемной плотности энергии (энергии единицы объема) электростатического поля
В случае неоднородного поля его энергия в объеме V находится интегрированием (15.9) по объему V пространства, занимаемого полем
Решение задач
ЗАДАЧА 6.
(r 1 или r 2). Тогда
ЗАДАЧА 7
ЗАДАЧА 8
Теоретическое введение 6 ЗАДАЧА 9
ЗАДАЧА 10
РЕШЕНИЕ
ЗАДАЧА 11
Теоретическое введение 7
|


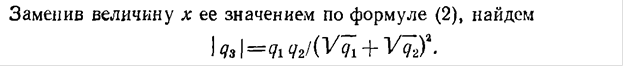

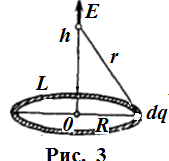 Решение. Разобьём кольцо на элементарные точечные заряды d q. Запишем потенциал точечного заряды d q в т. А. По (4.11)
Решение. Разобьём кольцо на элементарные точечные заряды d q. Запишем потенциал точечного заряды d q в т. А. По (4.11)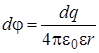
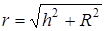 . Тогда
. Тогда ,
,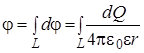
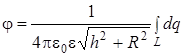 .
.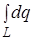 просто равен заряду полному q кольца q = t ∙ L = t ∙ 2 πr. Окончательно
просто равен заряду полному q кольца q = t ∙ L = t ∙ 2 πr. Окончательно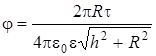
 РЕШЕНИЕ.
РЕШЕНИЕ.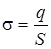 Применим теорему Гаусса для определения напряженности поля равномерно заряженной бесконечной плоскости. В этом случае ее поверхностная плотность заряда
Применим теорему Гаусса для определения напряженности поля равномерно заряженной бесконечной плоскости. В этом случае ее поверхностная плотность заряда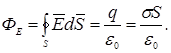
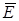 можно выразить через напряженность электрического поля у обоих оснований цилиндра, т.е.
можно выразить через напряженность электрического поля у обоих оснований цилиндра, т.е.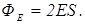
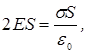
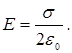 (1.26)
(1.26)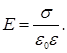 (1.27)
(1.27) (r 1 или r 2). Тогда
(r 1 или r 2). Тогда








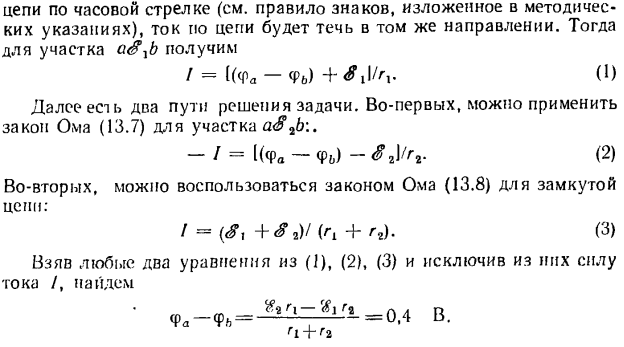



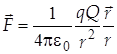 , (1.2)
, (1.2) - радиус - вектор, направленный к частице, на которую действует сила
- радиус - вектор, направленный к частице, на которую действует сила  , из точки, где находится другая частица, e 0 = 8,85×10-12 Кл2/(Нм2) - электрическая постоянная.
, из точки, где находится другая частица, e 0 = 8,85×10-12 Кл2/(Нм2) - электрическая постоянная.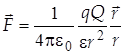 , (1.3)
, (1.3)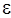 - диэлектрическая проницаемость среды. Безразмерная физическая величина
- диэлектрическая проницаемость среды. Безразмерная физическая величина 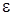 показывает во сколько раз кулоновское взаимодействие между двумя точечными электрическими зарядами в данной среде меньше, чем в вакууме. Подробнее величина
показывает во сколько раз кулоновское взаимодействие между двумя точечными электрическими зарядами в данной среде меньше, чем в вакууме. Подробнее величина 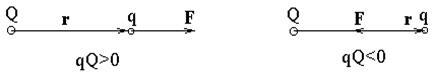
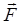 = q
= q 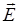 , (2.1)
, (2.1)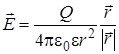 , (2.4)
, (2.4)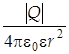 . (2.5)
. (2.5)
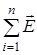 . (2.6)
. (2.6)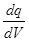 , где dq - заряд, заключенный в малом объеме dV. Тогда
, где dq - заряд, заключенный в малом объеме dV. Тогда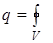 r dV (3.1)
r dV (3.1)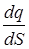 , где dq - заряд, находящийся на малом элементе dS. Тогда
, где dq - заряд, находящийся на малом элементе dS. Тогда s dS (3.2)
s dS (3.2) , где dq - заряд, заключенный на малом отрезке dl. Тогда
, где dq - заряд, заключенный на малом отрезке dl. Тогда . (3.3)
. (3.3)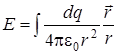 (3.4)
(3.4)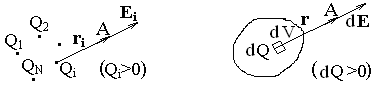
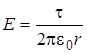 ; (3.5)
; (3.5)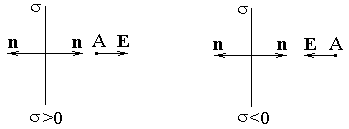
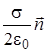 , (3.6)
, (3.6) - единичный вектор, перпендикулярный плоскости (рис.3.2).
- единичный вектор, перпендикулярный плоскости (рис.3.2).
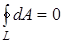 , (4.2)
, (4.2)
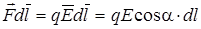 - элементарная работа сил поля на перемещении
- элементарная работа сил поля на перемещении 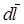 (помним?, что интеграл по смыслу просто сумма элементарных, т.е. малых величин). Силовое поле, обладающее свойством (4.2), является потенциальным. Подставив dA в (4.2), получим
(помним?, что интеграл по смыслу просто сумма элементарных, т.е. малых величин). Силовое поле, обладающее свойством (4.2), является потенциальным. Подставив dA в (4.2), получим (4.3)
(4.3)
 называется циркуляцией вектора напряженности.
называется циркуляцией вектора напряженности.
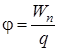 . (4.6)
. (4.6)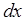 равна q
равна q 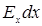 . С другой стороны, эту работу можно выразить через разность потенциалов на концах отрезка
. С другой стороны, эту работу можно выразить через разность потенциалов на концах отрезка 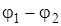 ) =- q
) =- q  . Приравнивая оба выражения для работы, получим
. Приравнивая оба выражения для работы, получим 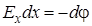 , откуда связь потенциала с напряженности электростатического поля имеет вид
, откуда связь потенциала с напряженности электростатического поля имеет вид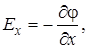 (4.7)
(4.7)
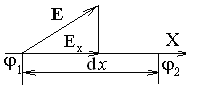 где частная производная соответствует дифференцированию только по перемещению по оси х (рис.4.1). Найдя по аналогии с (4.8) проекции вектора
где частная производная соответствует дифференцированию только по перемещению по оси х (рис.4.1). Найдя по аналогии с (4.8) проекции вектора 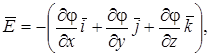 (4.8)
(4.8)  единичные векторы координатных осей x, y и z.
единичные векторы координатных осей x, y и z.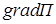 ) и формулу (4.8) записывают в виде
) и формулу (4.8) записывают в виде (4.9)
(4.9)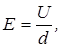 (4.10)
(4.10) электростатического поля в объеме и на поверхности проводника равна нулю
электростатического поля в объеме и на поверхности проводника равна нулю 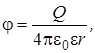 (4.11)
(4.11)
 (4.12)
(4.12)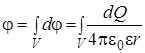 . (4.12а)
. (4.12а)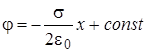 . (4.13)
. (4.13)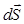 называется dS × n, а элементарным потоком d Ф вектора Е через площадку dS
называется dS × n, а элементарным потоком d Ф вектора Е через площадку dS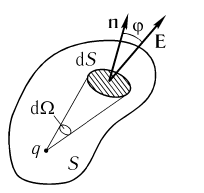 d Ф = (Е d S) = (E n) dS = E cosj dS. (5.1)
d Ф = (Е d S) = (E n) dS = E cosj dS. (5.1)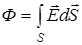 . (5.2)
. (5.2)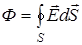 (5.3)
(5.3)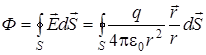 . (5.4)
. (5.4) совпадают по направлению и
совпадают по направлению и 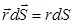 , а величина поля Е (2.4) одинакова по всей поверхности. Тогда вычисление интеграла (1.8) упрощается
, а величина поля Е (2.4) одинакова по всей поверхности. Тогда вычисление интеграла (1.8) упрощается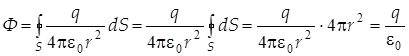 . (5.5)
. (5.5)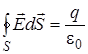 . (5.6)
. (5.6)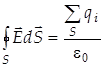 . (5.7)
. (5.7)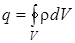 и (5.7) для этого случая запишется
и (5.7) для этого случая запишется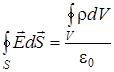 . (5.8)
. (5.8)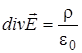 . (5.9)
. (5.9) §7. Электрический диполь.
§7. Электрический диполь. называется произведение положительного заряда на плечо диполя:
называется произведение положительного заряда на плечо диполя: (7.1)
(7.1) Ом·м, тогда как у металлических проводников ρ М~
Ом·м, тогда как у металлических проводников ρ М~  Ом·м. По этому признаку легко отличить диэлектрики от проводников. Различие в сопротивлении обусловлено большим количеством свободных зарядов в проводниках (электронов или ионов), способных под действием электрического поля приходить в упорядоченное движение и перемещаться на значительные расстояния. В атомах и молекулах диэлектриков тоже есть заряженные частицы – электроны и протоны, но они связаны кулоновскими силами притяжения так прочно, что в отсутствии ионизации они могут лишь незначительно сместиться под действием электрического поля друг относительно друга. Поэтому заряды в молекулах диэлектрикахназывают связанными и обозначают со штрихом (q ´). С точки зрения способности создавать электрическое поле свободные и связанные заряды неразличимы.
Ом·м. По этому признаку легко отличить диэлектрики от проводников. Различие в сопротивлении обусловлено большим количеством свободных зарядов в проводниках (электронов или ионов), способных под действием электрического поля приходить в упорядоченное движение и перемещаться на значительные расстояния. В атомах и молекулах диэлектриков тоже есть заряженные частицы – электроны и протоны, но они связаны кулоновскими силами притяжения так прочно, что в отсутствии ионизации они могут лишь незначительно сместиться под действием электрического поля друг относительно друга. Поэтому заряды в молекулах диэлектрикахназывают связанными и обозначают со штрихом (q ´). С точки зрения способности создавать электрическое поле свободные и связанные заряды неразличимы.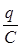 , (14.3)
, (14.3)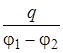 . (14.4)
. (14.4) . (14.7)
. (14.7)
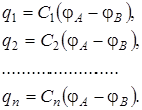

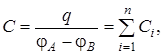 (14.8)
(14.8)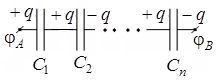
 батареи.
батареи.
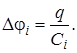

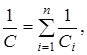 (14.9)
(14.9) батареи всегда меньше наименьшей емкости конденсатора, используемого в батарее.
батареи всегда меньше наименьшей емкости конденсатора, используемого в батарее.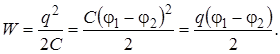 (15.6)
(15.6) пространства, занимаемого полем
пространства, занимаемого полем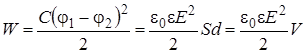 , (15.8)
, (15.8)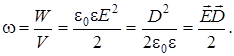 (15.9)
(15.9)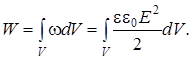 (15.10)
(15.10)


