
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Введение: задача распознавания речиСодержание книги
Поиск на нашем сайте
Распознавание речи Курс лекций по дисциплине «Распознавание речи» для студентов магистратуры, обучающихся по направлению подготовки 09.04.01 – «Информатика и вычислительная техника»
Донецк – 2016 Лекция 1 Тема. Классификация и общая структура систем распознавания речи, подходы к их разработке. В лекции будет рассмотрено: Классификация систем распознавания речи. Речевые базы данных. Архитектура систем распознавания речи. Проблемы, возникающие при разработке систем распознавания речи. Наиболее распространенный подход к распознаванию речи Упрощенно процесс распознавания речи может быть описан в виде последовательности следующих основных шагов. Шумоочистка и отделение полезного сигнала. Методы, применяемые для решения данной задачи, можно условно разделить на четыре группы. Методы первой группы обычно сводятся либо к выделению некоторых инвариантных относительно шума признаков, либо к обучению в условиях шумов или модификации эталонов распознавания с использованием оценки уровня шумов. Узким местом подобных методов является поразительный эффект ненадежной работы систем распознавания, настроенных на распознавание в шуме, в условиях отсутствия шумов. Преобразование входного речевого сигнала в набор акустических параметров. Как отмечалось выше, обычно звуковой сигнал разбивают на окна одинаковой длины и преобразуют в частотную область с помощью дискретного преобразования Фурье или более сложного преобразования, после чего частотные параметры факторизуют с целью сокращения размерности. По физическому смыслу частотные параметры наиболее близки к тем, которые использует человек в процессе восприятия речи. Лекция 2 Тема. Способы параметризации речевого сигнала На лекции будет рассмотрено: Дискретизация звука. Амплитудно-временное представление (АВП) сигнала. Спектральное представление сигнала. Спектры Фурье и вейвлет-спектры.
Ключевые операции ЦОС Цифровая обработка сигналов (ЦОС) выполняется либо специальными процессорами, либо на универсальных ЭВМ и компьютерах по специальным программам. Наиболее просты для рассмотрения линейные системы. Линейными называются системы, для которых имеет место суперпозиция (отклик на сумму двух входных сигналов равен сумме откликов на эти сигналы по отдельности) и однородность, или гомогенность (отклик на входной сигнал, усиленный в определенное число раз, будет усилен в то же число раз). Линейность позволяет рассматривать объекты исследования по частям, а однородность - в удобном масштабе. Для реальных объектов свойства линейности могут выполняться приближенно и в определенном интервале входных сигналов.
Если входной сигнал x (t - t 0) порождает одинаковый выходной сигнал y (t - t 0) при любом сдвиге t 0, то систему называют инвариантной во времени. Ее свойства можно исследовать в любые произвольные моменты времени. Для описания линейной системы вводится специальный входной сигнал - единичный импульс (импульсная функция). В силу свойства суперпозиции и однородности любой входной сигнал можно представить в виде суммы таких импульсов, подаваемых в разные моменты времени и умноженных на соответствующие коэффициенты. Выходной сигнал системы в этом случае представляет собой сумму откликов на эти импульсы, умноженных на указанные коэффициенты. Отклик на единичный импульс называют импульсной характеристикой системы h (n), а отклик на произвольный входной сигнал s (k) можно выразить сверткой g (k) = h (n)* s (k - n). Если h (n)=0 при n <0, то систему называют каузальной (причинной). В такой системе реакция на входной сигнал появляется только после поступления сигнала на ее вход. Некаузальные системы реализовать физически невозможно. Если требуются физически реализовать свертку сигналов с двусторонними операторами (при дифференцировании, преобразовании Гильберта, и т.п.), то это выполняется с задержкой (сдвигом) входного сигнала минимум на длину левосторонней части оператора свертки. Существует большое количество разнообразных алгоритмов ЦОС, еще больше находится в стадии разработки или ждет своего открывателя. Однако для всех этих алгоритмов, включая самые сложные, необходимы одни и те же основные операции. Для начала будет полезно рассмотреть некоторые из них, чтобы оценить простоту реализации ЦОС. Итак, основные операции ЦОС — это свертка, корреляция, фильтрация, дискретные преобразования. Дадим краткое описание каждой из них. При этом заметим, что для всех основных операций ЦОС потребуется выполнение только простых арифметических действий — умножения, сложения, вычитания и операции сдвига. Кроме того, отметим сходство между многими операциями.
Свертка Свертка — это одна из наиболее используемых операций в ЦОС. Например, это основная операция цифровой фильтрации. Для двух массивов x (n) и h (n) длиной
где Если h (n) трактовать как импульсную характеристику линейной цифровой системы, значения отсчетов которой приведены в таблице 1, а x (n) - как сигнал на входе цифровой системы (см.табл.2), тогда массив y (n) представляет собой сигнал на выходе линейной цифровой системы (см.табл.3). Действительно, учитывая финитность данных конкретных массивов, соотношение (4.1) можно переписать в виде:
Для
Для
Продолжая таким образом вычисления и учитывая, что
Таблица 1
Таблица 2
Таблица 3
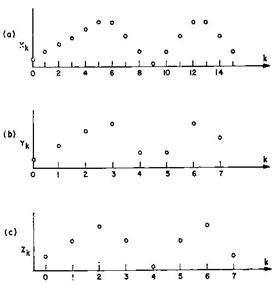
0 1 2 3 4
0 1 2 3 4
0 1 2 3 4 Рис.2.1 Цифровая фильтрация Цифровая фильтрация для одной из разновидностей цифровых фильтров – так называемых КИХ-фильтров (трансверсальных фильтров), математически описывается соотношением:
Сравнивая соотношения (2.2) и (2.3), нетрудно заметить их принципиальное сходство. Таким образом, цифровая фильтрация есть свертка сигнала с импульсной характеристикой фильтра. На рис.2.2 показана блок-схема такого фильтра. Символом
Рис.2.2 Основное применение цифровой фильтрации – подавление помех, маскирующих сигнал. Однако существует ряд иных интересных применений цифровых фильтров: моделирование резонансных свойств речевого тракта человека, физическое моделирование музыкальных звуков, выравнивание сигнала (эквалайзинг) и др. Корреляция Корреляциясуществует в двух формах: автокорреляции и взаимной корреляции. Взаимно-корреляционная функция (ВКФ, cross-correlation function - CCF), и ее частный случай для центрированных сигналов функция взаимной ковариации (ФВК)– это показатель степени сходства формы и свойств двух сигналов. Для двух последовательностей x (k) и y (k) длиной К с нулевыми средними значениями оценка взаимной ковариации выполняется по формулам:
ВКФ – это показатель степени сходства формы и свойств двух сигналов. Автокорреляционная функция (АКФ, correlation function, CF) является количественной интегральной характеристикой формы сигнала, дает информацию о структуре сигнала и его динамике во времени. Она, по существу, является частным случаем ВКФ для одного сигнала и представляет собой скалярное произведение сигнала и его копии в функциональной зависимости от переменной величины значения сдвига:
Нетрудно видеть известное сходство операций корреляции и свертки – разница лишь в том, что при свертке один из сигналов инвертируется, а при корреляции такой инверсии нет. Автокорреляционная функция успешно применяется для выявления так называемой «скрытой» периодичности сигнала. Взаимно-корреляционная функция применяется в задачах обнаружения сигнала известной формы, маскируемого помехами. Дискретные преобразования Дискретные преобразования позволяют описывать сигналы с дискретным временем в частотных координатах или переходить от описания во временной области к описанию в частотной. Переход от временных (пространственных) координат к частотным необходим во многих приложениях обработки данных. Дискретных преобразований достаточно много (преобразования Фурье, Хаара, Уолша, Гильберта и др.), однако самым распространенным является дискретное преобразование Фурье (ДПФ), с помощью которого осуществляют спектральный анализ сигналов:
Если соотношение (4.6) переписать в виде:
тогда становится очевидным, что ДПФ можно трактовать как результат цифровой фильтрации сигнала При достаточно большом значении параметра Модуляция сигналов Системы регистрации, обработки, интерпретации, хранения и использования информационных данных становятся все более распределенными, что требует коммуникации данных по высокочастотным каналам связи. Как правило, информационные сигналы являются низкочастотными и ограниченными по ширине спектра, в отличие от широкополосных высокочастотных каналов связи, рассчитанных на передачу сигналов от множества источников одновременно с частотным разделением каналов. Перенос спектра сигналов из низкочастотной области в выделенную для их передачи область высоких частот выполняется операцией модуляции. При модуляции значения информационного (модулирующего) сигнала переносятся на определенный параметр высокочастотного (несущего) сигнала.
Самые распространенные схемы модуляции для передачи цифровой информации по широкополосным каналам – это амплитудная (amplitude shift keying – ASK), фазовая (phase shift keying – PSK) и частотная (frequensy shift keying – FSK) манипуляции. При передаче данных по цифровым сетям используется также импульсно-кодовая модуляция (pulse code modulation – PCM).
Формы преобразования Фурье Непрерывное преобразование Фурье Известно несколько форм представления ряда Фурье: 1) синусно-косинусная; 2) амплитудно-фазовая; 3) комплексная. А. Синусно-косинусная форма Функция
где Здесь
Достоинство такого представления – вещественность величин Недостаток – не очень понятна необходимость функций Б. Амплитудно-фазовая форма Запишем (2.7) в виде:
Или, что то же,
Сравнивая с (5.1), видим, что:
откуда
В. Комплексная форма В амплитудно-фазовой форме полагаем:
Получаем:
Дискретное преобразование Фурье Пару непрерывных преобразований Фурье обычно записывают в виде:
Перепишем соотношения (2.8) в виде:
При
Можно рассуждать и по-иному. Сравним соотношения:
Если функция
Таким образом, с учетом соотношений (2.6) и (2.8) можем записать:
где обозначено
Используя дуальность времени t и частоты f, а также полученный выше результат о возможности формального перехода от пары непрерывных преобразований Фурье к паре дискретно-непрерывных преобразований Фурье, сразу запишем:
Продолжая развивать идею «дискретизации-периодизации», приходим к паре дискретных соотношений:
0
Обозначая
Быстрое преобразование Фурье (БПФ)
Пару ДПФ часто записывают в виде:
где
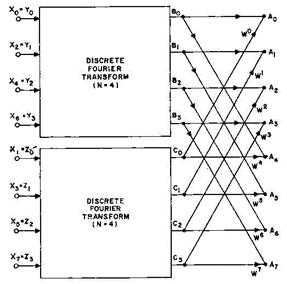
Для вычисления одного элемента последовательности Еще более заметен выигрыш алгоритма БПФ при обработке двумерных массивов чисел, например, при обработке изображений. В этом случае необходимо Существует несколько разновидностей алгоритма БПФ. Ниже будет изложена модификация алгоритма БПФ: с прореживанием по времени. Существует и вторая - с прореживанием по частоте. При этом рассмотрим случай, когда N - степень двойки. А. Прореживание по времени Разделим последовательность Отсчеты
Поскольку подпоследовательности
Нам нужна последовательность
Рис.2.3 Рис.2.4
Поскольку
Таким образом, первые
Рис.2.5 Рис.2.6
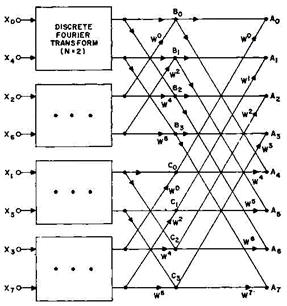
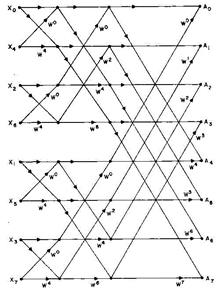
Поскольку нам удалось задачу вычисления N -точечного ДПФ редуцировать к задаче вычисления двух N /2-точечных ДПФ, естественно попытаться “развить” успех в данном направлении. На рис.2.5 и 2.6 показаны два следующих аналогичных шага, после которых отсчеты сигнала Итак, для случая N = 23 = 8 вычисления совершаются в 3 этапа. На первых двух этапах вычисляются некие “промежуточные” массивы из 8 точек каждый. На третьем этапе вычисляется “окончательный” 8-точечный массив. Для вычисления каждого элемента этих 3-х массивов необходимо выполнить одно комплексное умножение и одно комплексное сложение – итого Обобщая наши рассуждения на случай N -точечных массивов, заключаем, что для вычислений в соответствии с алгоритмом БПФ необходимо N log2 N комплексных умножений и сложений, тогда как при прямых вычислениях требуется N операций. Таким образом, при прореживании по частоте, как и при прореживании по времени, процедуру вычислений делят наlog2 N этапов. При этом на каждом этапе на вычисление элементов N -точечного массива затрачивается N комплексных сложений и умножений. В результате вычисления производятся примерно за N log2 N комплексных сложений и умножений против N 2 при “лобовых” вычислениях. Признаки вейвлета Для практического применения важно знать признаки, которыми обязательно должна обладать функция, чтобы быть вейвлетом: Локализация. Вейвлет должен быть локализован и во временном пространстве, и по частоте. Нулевое среднее:
Часто для приложений оказывается необходимым, чтобы первые
Такой вейвлет называется вейвлетом Ограниченность:
Опишем сигнал в терминах вейвлет-преобразования при помощи его средних (по некоторым интервалам) значений и изменений вокруг этих средних (флуктуациями). Это позволит вскрыть флуктуационную структуру сигнала на разных масштабах, что приводит к понятию многомасштабного анализа. Многомасштабный анализ Многомасштабное приближение 1. 2. 3. 4. С учетом многомасштабного анализа разложение функции в вейвлет-ряд имеет вид:
при этом Возвращаясь к вейвлетам, отметим, что Вейвлет-коэффициенты
Первая сумма в (1) со скейлинг-функциями Представление (2.14) взаимно однозначно для любой функции из Вейвлеты Добеши Свяжем функцию
Величина масштабирующего множителя определяет размер ячеек выбранной решетки, число
Если
В практических приложениях используются только вейвлет-коэффициенты Общие свойства скейлинг-функций и вейвлетов однозначно определяют коэффициенты Из свойства ортогональности масштабных функций:
Из ортогональности вейвлетов масштабным функциям:
Отсюда получим
т. е. Условие ортогональности вейвлетов полиномам до степени
Вообще говоря, чем больше моментов равны нулю, тем больше вейвлет-коэффициентов для гладких функций близки к нулю. Очевидно, число нулевых моментов важно для достижения более сильного сжатия сигнала. Условие нормировки:
Набор всех возможностей (2.17) - (2.20) задает полную систему вейвлетов данного порядка из известного семейства ортонормальных вейвлетов Добеши. Вейвлеты Добеши с компактным носителем определяются одн
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2022-09-03; просмотров: 83; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.91.59 (0.013 с.) |

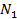 и
и 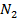 соответственно, их свертка определяется соотношением:
соответственно, их свертка определяется соотношением: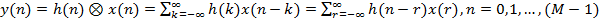 , (2.1)
, (2.1)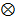 - символ свертки, а
- символ свертки, а 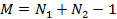 .
.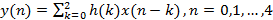 . (2.2)
. (2.2)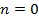 получим:
получим: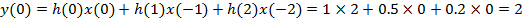 .
.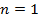 :
: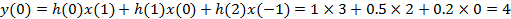 .
.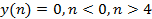 , получим результаты, сведенные в таблицу 3.
, получим результаты, сведенные в таблицу 3.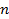
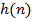
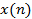

 Графически результаты вычисления свертки представлены на рис.2.1.
Графически результаты вычисления свертки представлены на рис.2.1.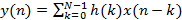 . (2.3)
. (2.3)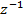 обозначена задержка на один интервал дискретизации.
обозначена задержка на один интервал дискретизации.
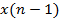
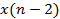
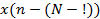
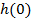
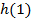
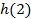
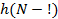
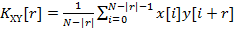 . (2.4)
. (2.4)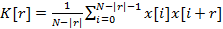 , (2.5)
, (2.5)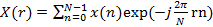 . (2.6)
. (2.6)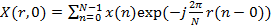 ,
,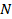 вычисление ДПФ весьма трудоемко. Благодаря изобретению алгоритма быстрого преобразования Фурье (БПФ) стало возможным весьма эффективное вычисление ДПФ (
вычисление ДПФ весьма трудоемко. Благодаря изобретению алгоритма быстрого преобразования Фурье (БПФ) стало возможным весьма эффективное вычисление ДПФ (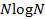 арифметических операций вместо
арифметических операций вместо 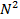 операций).
операций).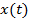 - периодическая с периодом
- периодическая с периодом 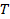 . «Классическая» синусно-косинусная форма представления этой функции в виде ряда Фурье имеет вид:
. «Классическая» синусно-косинусная форма представления этой функции в виде ряда Фурье имеет вид: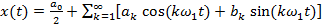 , (2.7)
, (2.7)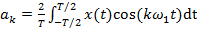 ,
, 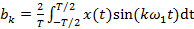 .
.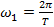 - «основная» частота ряда частот
- «основная» частота ряда частот 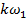 гармоник, на которые раскладывается сигнал
гармоник, на которые раскладывается сигнал 


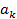
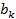
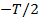 0
0 
 0 1 2 3
0 1 2 3 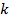 0 1 2 3
0 1 2 3 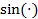 и
и 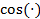 .
.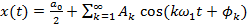 . (5.2)
. (5.2)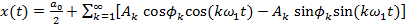 .
.
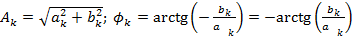 .
.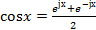 .
.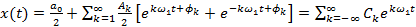 ; (2.8а)
; (2.8а)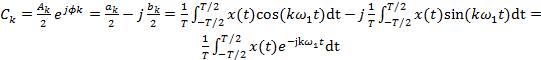 (2.8б)
(2.8б)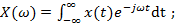 (2.9а)
(2.9а)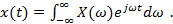 (2.9б)
(2.9б)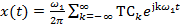 ;
;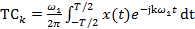 .
.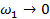 эти соотношения превращаются в пару непрерывных преобразований Фурье, поэтому:
эти соотношения превращаются в пару непрерывных преобразований Фурье, поэтому: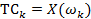 (2.10)
(2.10)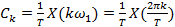 .
.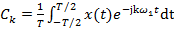 ;
;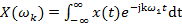 .
.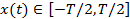 , тогда, периодизируя ее, можем записать:
, тогда, периодизируя ее, можем записать: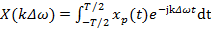 ; (2.11а)
; (2.11а)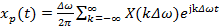 , (2.11б)
, (2.11б)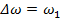 . Сравнивая пары соотношений (2.9) и (2.11), видим, что пару (5.6) можно формально и абсолютно точно получить, заменяя в (2.9а) бесконечные пределы интегрирования на конечные, а в (2.9б) – заменяя интеграл суммой. Причина точности произведенной замены – периодическое продолжение функции времени, приводящее к дискретизации спектра. Чтобы подчеркнуть периодический характер функции времени, мы и применили обозначение
. Сравнивая пары соотношений (2.9) и (2.11), видим, что пару (5.6) можно формально и абсолютно точно получить, заменяя в (2.9а) бесконечные пределы интегрирования на конечные, а в (2.9б) – заменяя интеграл суммой. Причина точности произведенной замены – периодическое продолжение функции времени, приводящее к дискретизации спектра. Чтобы подчеркнуть периодический характер функции времени, мы и применили обозначение 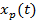 .
.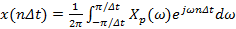 ; (2.12а)
; (2.12а)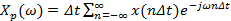 , (2.12б)
, (2.12б)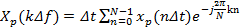 ;
;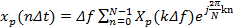 , где
, где 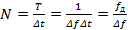 .
.

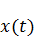
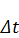
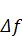
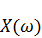
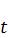 -
- 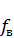
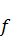
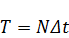
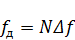
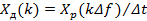 , получим «классическую» пару дискретных преобразований Фурье (ДПФ):
, получим «классическую» пару дискретных преобразований Фурье (ДПФ):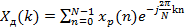 ; (2.13а)
; (2.13а)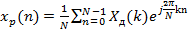 (2.13а)
(2.13а)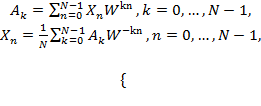
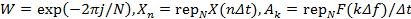 ,
, - отсчеты сигнала,
- отсчеты сигнала, 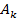 - коэффициенты ДПФ.
- коэффициенты ДПФ.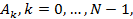 необходимо примерно
необходимо примерно 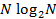 . Преимущества алгоритма БПФ быстро увеличиваются с ростом N, что существенно при обработке массивов большой размерности.
. Преимущества алгоритма БПФ быстро увеличиваются с ростом N, что существенно при обработке массивов большой размерности.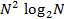 операций против
операций против 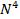 при «лобовых» вычислениях.
при «лобовых» вычислениях.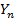 и
и 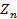 , каждая из N/ 2 отсчетов (рис.5.3).
, каждая из N/ 2 отсчетов (рис.5.3).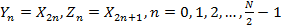 .
. 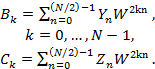
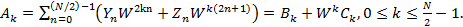
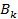 и
и 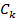 периодичны с периодом
периодичны с периодом 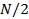 , можем записать:
, можем записать: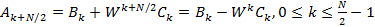 .
. 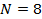 .
.
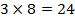 комплексных умножений и сложений вместо
комплексных умножений и сложений вместо 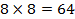 комплексных умножений и сложений при “лобовых” вычислениях.
комплексных умножений и сложений при “лобовых” вычислениях.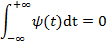
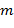 моментов были равны 0:
моментов были равны 0: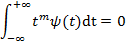
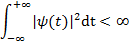
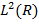 представляет собой нарастающую последовательность
представляет собой нарастающую последовательность 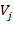 замкнутых линейных пространств
замкнутых линейных пространств 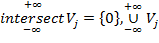 всюду плотно в
всюду плотно в 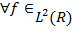 и
и 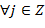
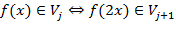 ;
;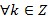
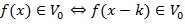 ;
;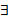 такая функция
такая функция 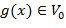 что последовательность
что последовательность 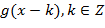 является ортонормальным базисом Рисса в пространстве
является ортонормальным базисом Рисса в пространстве 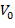 .
.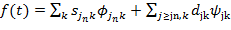 (2.14)
(2.14)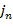 является уровнем детализации,
является уровнем детализации, 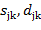 - коэффициенты вейвлет-разложения,
- коэффициенты вейвлет-разложения, 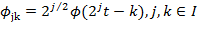 ,
, 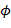 - скейлинг-функция или масштабная функция,
- скейлинг-функция или масштабная функция, 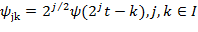 ,
, 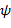 - базисный или «материнский» вейвлет. Эти коэффициенты зачастую называют суммами (
- базисный или «материнский» вейвлет. Эти коэффициенты зачастую называют суммами (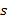 ) и разностями (
) и разностями (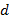 ), связывая со средними значениями и флуктуациями соответственно.
), связывая со средними значениями и флуктуациями соответственно.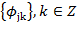 образуют ортонормированный базис
образуют ортонормированный базис 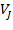 ;
; 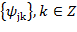 образуют ортонормированный базис в
образуют ортонормированный базис в 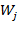 , где
, где 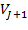 . Полный набор
. Полный набор 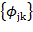 и
и 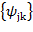 при всех
при всех 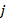 образуют ортонормированный базис в
образуют ортонормированный базис в 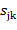 и
и 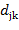 можно вычислить по формулам:
можно вычислить по формулам: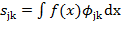 (2.15)
(2.15)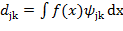 (2.16)
(2.16)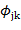 содержит средние значения
содержит средние значения 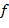 по диадным интервалам
по диадным интервалам 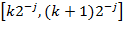 (усреднение проводится с весовыми функциями
(усреднение проводится с весовыми функциями 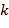 -том отрезке). Второй член содержит все флуктуации
-том отрезке). Второй член содержит все флуктуации 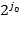 , где
, где 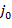 - начальный уровень с наименьшими интервалами, число членов в каждой сумме зависит от выбранного уровня разрешения. На
- начальный уровень с наименьшими интервалами, число членов в каждой сумме зависит от выбранного уровня разрешения. На 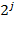
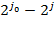
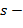 коэффициенты и получается представление скейлинг-функцией, конечное представление улавливает все флуктуации, имеющиеся в сигнале. При практическом анализе сигналов скейлинг- и вейвлет-функции называют широкополосными и узко-полосными фильтрами, т. к. они отфильтровывают компоненты сигнала на больших и малых масштабах.
коэффициенты и получается представление скейлинг-функцией, конечное представление улавливает все флуктуации, имеющиеся в сигнале. При практическом анализе сигналов скейлинг- и вейвлет-функции называют широкополосными и узко-полосными фильтрами, т. к. они отфильтровывают компоненты сигнала на больших и малых масштабах.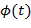 с ее сдвинутыми и сжатыми модификациями. Простейшее линейное соотношение с числом коэффициентов
с ее сдвинутыми и сжатыми модификациями. Простейшее линейное соотношение с числом коэффициентов 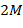 можно записать в виде:
можно записать в виде: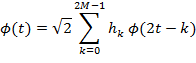
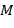 - число коэффициентов
- число коэффициентов 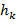 и длину области задания вейвлета. Для ортонормированных базисов
и длину области задания вейвлета. Для ортонормированных базисов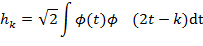
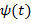 по формуле:
по формуле: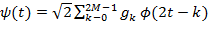 , где
, где 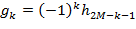 . Связь
. Связь 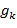 и
и 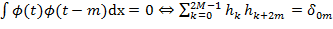 (2.17)
(2.17)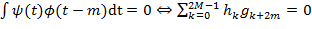
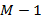 :
: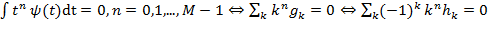 (2.19)
(2.19)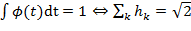 (2.20)
(2.20)


