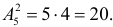Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сочетанием без повторений из n элементов по k называется любое k-элементное подмножество заданного n-элементного множества.Содержание книги
Поиск на нашем сайте Например, из множества {a, b, c, d} можно составить следующие сочетания без повторений из трех элементов: {a, b, c}, {a, b, d}, {a, c, d}, {b, c, d}. Количество сочетаний без повторений из n элементов по k элементов обозначается символом Выясним, сколько всего можно составить сочетаний без повторений из n элементов по k. Для этого используем известные нам формулы числа размещений и перестановок. Составление размещения без повторений из n элементов по k проведем в два этапа. Сначала выберем k разных элементов из заданного n-элементного множества, не учитывая порядок выбора этих элементов (то есть выберем kэлементное подмножество из n-элементного множества — сочетание без повторений из n-элементов по k). По нашему обозначению это можно сделать
Например, Используя формулу (3), можно легко обосновать свойство 1 числа сочетаний без повторений, приведенное в табл. 28. 1) Поскольку
Для того чтобы формулу (4) можно было использовать и при k = n, договорились считать, что Заметим, что формулу (4) можно получить без вычислений с помощью достаточно простых комбинаторных рассуждений. Когда мы выбираем k предметов из n, то n – k предметов мы оставляем. Если же, напротив, выбранные предметы оставим, а другие n – k -выберем, то получим способ выбора n – k предметов из n. Мы получили взаимно-однозначное соответствие способов выбора k и n – k предметов из n. Значит, количество одних и других способов одинаково. Но количество одних — Если в формуле (3) сократить числитель и знаменатель на (n – k)!, то получим формулу, по которой удобно вычислять
Например, 2. Вычисление числа сочетаний без повторений с помощью треугольника Паскаля: Для вычисления числа сочетаний без повторений можно применять формулу (3):
Для обоснования равенства (6) можно записать сумму
Это равенство позволяет последовательно вычислять значения
Каждая строка этой таблицы начинается с единицы и заканчивается единицей Если какая-либо строка уже заполнена, например третья, то в четвертой строке надо записать на первом месте единицу. На втором месте запишем число, равное сумме двух чисел третьей строки, стоящих над ним левее и правее (поскольку по формуле (6) Примеры решения задач: Обратим внимание, что, как и раньше, для выбора формулы при решении простейших комбинаторных задач достаточно ответить на вопросы: 1. Учитывается ли порядок следования элементов в соединении? 2. Все ли заданные элементы входят в полученное соединение? Чтобы выяснить, является ли заданное соединение сочетанием, достаточно ответить только на первый вопрос (см. схему в табл. 28). Если порядок следования элементов не учитывается, то по определению это сочетание из n элементов по k элементов. Пример: Из 12 членов туристической группы надо выбрать трех дежурных. Сколькими способами можно сделать этот выбор? Решение: Количество способов выбрать из 12 туристов трех дежурных равно количеству сочетаний из 12 элементов по 3 (без повторений), то есть Комментарий: Для выбора соответствующей формулы выясняем ответы на вопросы, приведенные выше. Поскольку порядок следования элементов не учитывается (для дежурных неважно, в каком порядке их выберут), то соответствующее соединение является сочетанием из 12 элементов по 3 (без повторений). Для вычисления можно использовать формулы (3) или (5), в данном случае применяем формулу (3): Пример: Из вазы с фруктами, в которой лежат 10 разных яблок и 5 разных груш, требуется выбрать 2 яблока и 3 груши. Сколькими способами можно сделать такой выбор? Решение: Выбрать 2 яблока из 10 можно Комментарий: Сначала отдельно выберем 2 яблока из 10 и 3 груши из 5. Поскольку при выборе яблок или груш порядок следования элементов не учитывается, то соответствующие соединения — сочетания без повторений. Учитывая, что требуется выбрать 2 яблока и 3 груши, используем правило произведения и перемножим полученные возможности выбора яблок Бином Ньютона:
Поскольку
Общий член разложения степени бинома имеет вид
Свойства биномиальных коэффициентов: 1. Число биномиальных коэффициентов (а следовательно, и число слагаемых) в разложении n-й степени бинома равно n + 1. 2. Коэффициенты членов, равноудаленных от начала и конца разложения, равны между собой (поскольку 3. Сумма всех биномиальных коэффициентов равна 4. Сумма биномиальных коэффициентов, стоящих на четных местах, равна сумме биномиальных коэффициентов, стоящих на нечетных местах. 5. Для вычисления биномиальных коэффициентов можно воспользоваться треугольником Паскаля, в котором вычисления коэффициентов основываются на формуле
Объяснение и обоснование: Бином Ньютона: Двучлен вида a + x также называют биномом. Из курса алгебры известно, что:
Можно заметить, что коэффициенты разложения степени бинома
Формулу (7) называют биномом Ньютона. Правая часть этого равенства называется разложением степени бинома Общий член разложения степени бинома имеет вид
Обосновать формулу (7) можно, например, с помощью метода математической индукции. (Проведите такое обоснование самостоятельно.) Приведем также комбинаторные рассуждения для обоснования формулы бинома Ньютона. По определению степени с натуральным показателем Именно из-за бинома Ньютона числа Записывая степень двучлена по формуле бинома Ньютона для небольших значений n, биномиальные коэффициенты можно вычислять с помощью треугольника Паскаля (см. табл. 30). Например, Так как
Если в формуле бинома Ньютона (8) заменить x на (–x), то получим формулу возведения в степень разности a – x:
Например, Свойства биномиальных коэффициентов: 1. Число биномиальных коэффициентов (а следовательно, и число слагаемых) в разложении n-й степени бинома равно n + 1, поскольку разложение содержит все степени x от 0 до n (и других слагаемых не содержит). 2. Коэффициенты членов, равноудаленных от начала и конца разложения, равны между собой, поскольку 3. Сумма всех биномиальных коэффициентов равна Для обоснования полагаем в равенстве (7) значения a = x = 1 и получаем:
Например, 4. Сумма биномиальных коэффициентов, стоящих на четных местах, равна сумме биномиальных коэффициентов, стоящих на нечетных местах. Для обоснования возьмем в равенстве (7) значения a = 1, x = –1:
Тогда Примеры решения задач: Пример: По формуле бинома Ньютона найдите разложение степени Комментарий: Для нахождения коэффициентов разложения можно использовать треугольник Паскаля (табл. 30) или вычислять их по общей формуле. По треугольнику Паскаля коэффициенты равны: 1, 6, 15, 20, 15, 6, 1. Учитывая, что при возведении разности в степень знаки членов разложения чередуются, получаем:
Для упрощения записи ответа можно избавиться от иррациональности в знаменателях полученных выражений (см. решение) или сначала учесть, что ОДЗ данного выражения: x > 0. Тогда Решение:
Пример: В разложении степени Решение: ОДЗ: b > 0. Тогда
Общий член разложения: По условию член разложения должен содержать Тогда член разложения, содержащий
Комментарий: На ОДЗ (b > 0) каждое слагаемое в данном двучлене можно записать как степень с дробным показателем. Это позволит проще записать общий член разложения степени
(где k = 0, 1, 2,..., n), выяснить, какой из членов разложения содержит
Всё о комбинаторике Пусть имеется несколько множеств элементов:
Вопрос: сколькими способами можно составить новое множество Элемент
Способы выбора трех элементов аbc перечислены в табл. 1.2.
В этой таблице Основной комбинаторный принцип. Если некоторый первый выбор можно сделать Комбинаторные формулы в прикладных задачах теории вероятностей обычно связывают с выбором
При повторном выборе каждый по порядку элемент может быть выбран В случае бесповторной выборки первый элемент можно выбрать
Число Например, существует Выделим особо случай, когда один за другим выбраны все
называют числом перестановок из Например, пять человек могут встать в очередь Подсчитаем количество бесповторных выборок объема
Это число называют числом сочетаний из
Например, сочетаний из четырех элементов Так как из Величины
Из формулы (1.3) следует, что
Биномиальные коэффициенты образуют так называемый треугольник Паскаля, который имеет вид:
В Биномиальные коэффициенты обладают свойством симметрии:
Это наглядно демонстрирует треугольник Паскаля. Равенство (1.4) подтверждает тот очевидный факт, что выбор При повторном выборе из
Совокупность из Пусть
Для безошибочного выбора комбинаторной формулы достаточно последовательно ответить на вопросы в следующей схеме:
Например, число словарей, необходимых для непосредственного перевода с одного на другой, для пяти языков определяется из следующих рассуждений. Для составления словаря выбираем из пяти языков (
|
||
|
Последнее изменение этой страницы: 2022-01-22; просмотров: 273; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.012 с.) |

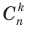 (читается: «число сочетаний из п по k» или «це из п по k», С — первая буква французского слова combinaison — сочетание). Как видим,
(читается: «число сочетаний из п по k» или «це из п по k», С — первая буква французского слова combinaison — сочетание). Как видим, 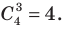
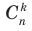 способами. После этого полученное множество из k разных элементов упорядочим. Его можно упорядочить
способами. После этого полученное множество из k разных элементов упорядочим. Его можно упорядочить 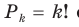 способами. Получим размещения без повторений из n элементов по k. Следовательно, количество размещений без повторений из n элементов по k в k! раз больше числа сочетаний без повторений из n элементов по k, то есть
способами. Получим размещения без повторений из n элементов по k. Следовательно, количество размещений без повторений из n элементов по k в k! раз больше числа сочетаний без повторений из n элементов по k, то есть 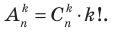 Отсюда
Отсюда 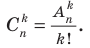 Учитывая, что по формуле (2)
Учитывая, что по формуле (2) 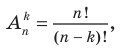 , получаем:
, получаем: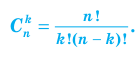 (3)
(3)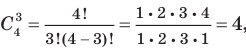 что совпадает со значением, полученным выше.
что совпадает со значением, полученным выше.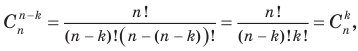 то
то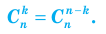 (4)
(4) Тогда
Тогда 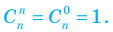
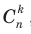 , а других
, а других 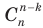 , поэтому
, поэтому 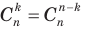 .
.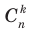 при малых значениях k:
при малых значениях k: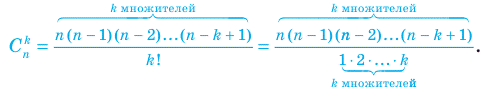 (5)
(5)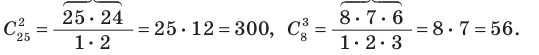
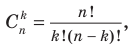 , а можно последовательно вычислять соответствующие значения, пользуясь следующим свойством:
, а можно последовательно вычислять соответствующие значения, пользуясь следующим свойством: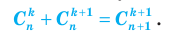 (6)
(6)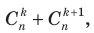 , используя формулу (3), и после приведения полученных дробей к общему знаменателю получить формулу для правой части равенства (6) (проделайте это самостоятельно). Также формулу (6) можно получить без вычислений с помощью комбинаторных рассуждений.
, используя формулу (3), и после приведения полученных дробей к общему знаменателю получить формулу для правой части равенства (6) (проделайте это самостоятельно). Также формулу (6) можно получить без вычислений с помощью комбинаторных рассуждений.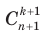 - это количество способов выбрать k +1 предмет из n + 1. Подсчитаем это количество, зафиксировав один предмет (назовем его «фиксированным»). Если мы не берем фиксированный предмет, то нам нужно выбрать k +1 предмет из n тех, что остались, а если мы его берем, то нужно выбрать из n тех, что остались, еще k предметов. Первое можно сделать
- это количество способов выбрать k +1 предмет из n + 1. Подсчитаем это количество, зафиксировав один предмет (назовем его «фиксированным»). Если мы не берем фиксированный предмет, то нам нужно выбрать k +1 предмет из n тех, что остались, а если мы его берем, то нужно выбрать из n тех, что остались, еще k предметов. Первое можно сделать 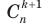 способами, второе
способами, второе 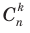 способами. Всего как раз
способами. Всего как раз 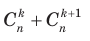 способов, следовательно,
способов, следовательно,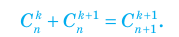
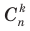 с помощью специальной таблицы, которая называется треугольником Паскаля. Если считать, что
с помощью специальной таблицы, которая называется треугольником Паскаля. Если считать, что 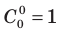 , то он будет иметь вид, представленный в табл. 29.
, то он будет иметь вид, представленный в табл. 29.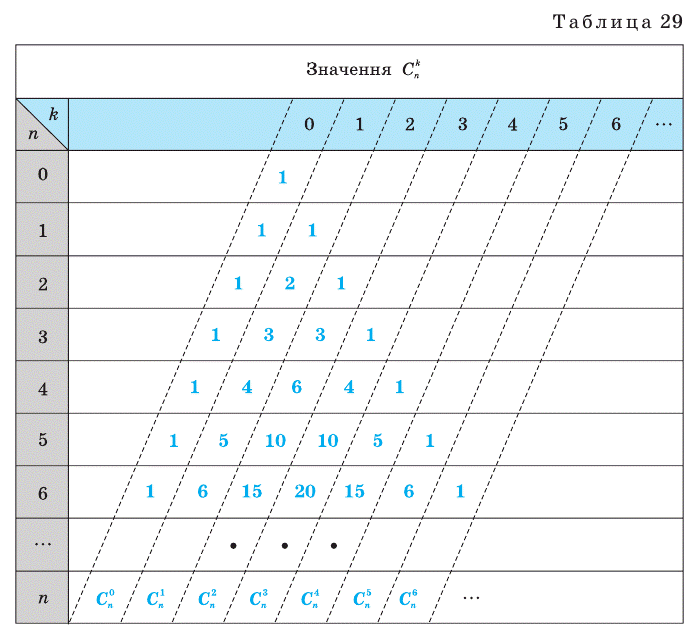
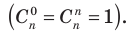
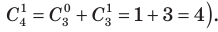 На третьем месте запишем число, равное сумме двух следующих чисел третьей строки, стоящих над ним левее и правее
На третьем месте запишем число, равное сумме двух следующих чисел третьей строки, стоящих над ним левее и правее 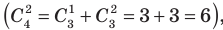 , и т. д. (а на последнем месте снова запишем единицу).
, и т. д. (а на последнем месте снова запишем единицу).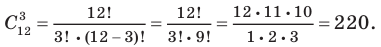
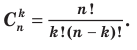
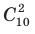 способами. При каждом выборе яблок груши можно выбрать
способами. При каждом выборе яблок груши можно выбрать 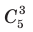 способами. Тогда по правилу произведения выбор требуемых фруктов можно выполнить
способами. Тогда по правилу произведения выбор требуемых фруктов можно выполнить 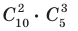 способами. Получаем
способами. Получаем 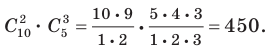
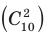 и груш
и груш 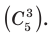
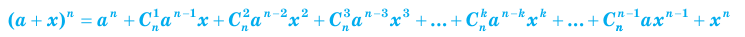
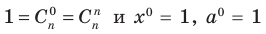 (при x ≠ 0 и a ≠ 0), то формулу бинома Ньютона можно записать еще и так:
(при x ≠ 0 и a ≠ 0), то формулу бинома Ньютона можно записать еще и так: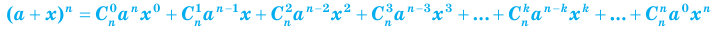
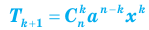 (где
(где 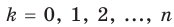 ). Коэффициенты
). Коэффициенты 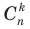 называют биномиальными коэффициентaми.
называют биномиальными коэффициентaми.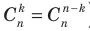 )
)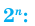
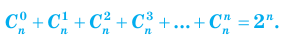
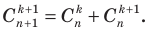
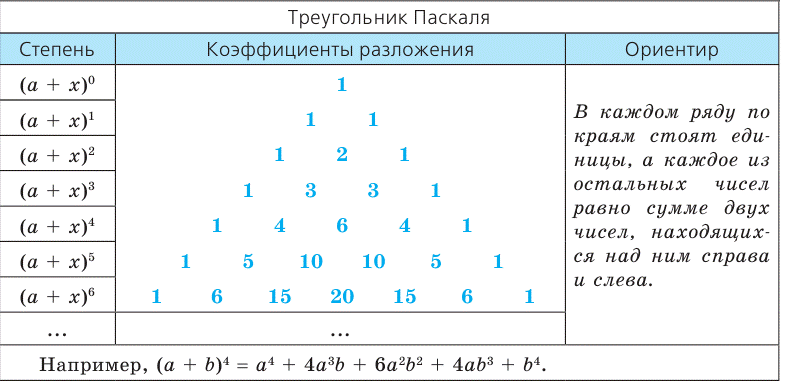
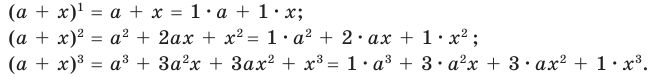
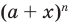 при n = 1, 2, 3 совпадают с числами в соответствующей строке треугольника Паскаля. Оказывается, что это свойство выполняется для любого натурального n, то есть справедлива формула
при n = 1, 2, 3 совпадают с числами в соответствующей строке треугольника Паскаля. Оказывается, что это свойство выполняется для любого натурального n, то есть справедлива формула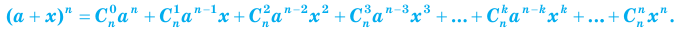 (7)
(7)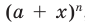 , а числа
, а числа 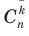 (при k = 0, 1, 2,..., n) называют биномиальными коэффициентами.
(при k = 0, 1, 2,..., n) называют биномиальными коэффициентами.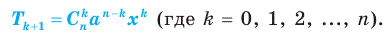
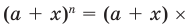
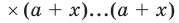 (всего n скобок). Раскрывая скобки, получаем в каждом слагаемом произведение n букв, каждая из которых - а или х. Если, например, в каком-либо слагаемом количество букв x равно k, то количество букв а в нем — n – k, то есть каждое слагаемое имеет вид
(всего n скобок). Раскрывая скобки, получаем в каждом слагаемом произведение n букв, каждая из которых - а или х. Если, например, в каком-либо слагаемом количество букв x равно k, то количество букв а в нем — n – k, то есть каждое слагаемое имеет вид 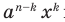 при некотором k от 0 до n. Покажем, что для каждого такого k число слагаемых an
при некотором k от 0 до n. Покажем, что для каждого такого k число слагаемых an 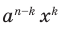 равно
равно 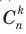 , откуда после приведения подобных членов и получаем формулу бинома. Произведение
, откуда после приведения подобных членов и получаем формулу бинома. Произведение 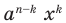 получаем, взяв букву x из k скобок и букву а из n – k тех скобок, которые остались. Разные такие слагаемые получим путем разного выбора первых k скобок, а k скобок из n можно выбрать именно
получаем, взяв букву x из k скобок и букву а из n – k тех скобок, которые остались. Разные такие слагаемые получим путем разного выбора первых k скобок, а k скобок из n можно выбрать именно 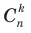 способами. Следовательно, общий член разложения бинома
способами. Следовательно, общий член разложения бинома 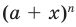 действительно имеет вид
действительно имеет вид 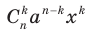 где k = 0, 1, 2,..., n.
где k = 0, 1, 2,..., n.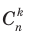 часто называют биномиальными коэффициентами.
часто называют биномиальными коэффициентами.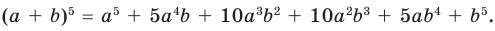
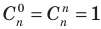 , формулу бинома Ньютона можно записать в виде:
, формулу бинома Ньютона можно записать в виде: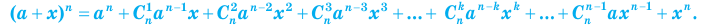 (8)
(8)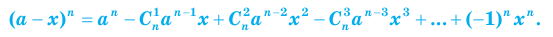
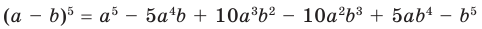 (знаки членов разложения чередуются!).
(знаки членов разложения чередуются!).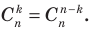
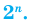
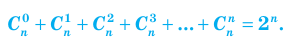
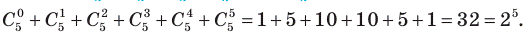
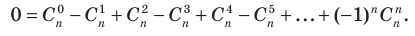
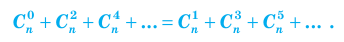
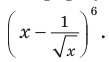 .
.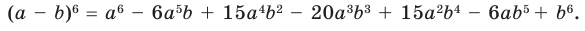
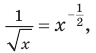 то есть данное выражение можно записать так:
то есть данное выражение можно записать так: 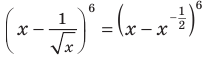 и возвести в степень последнее выражение.
и возвести в степень последнее выражение.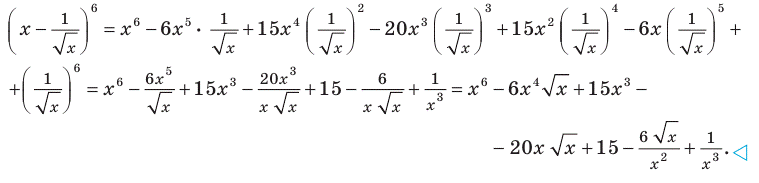
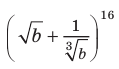 найдите член, содержащий
найдите член, содержащий 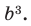
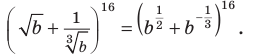 .
.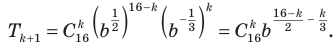
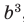 , следовательно,
, следовательно, 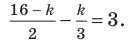 Отсюда k = 6.
Отсюда k = 6.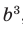 , равен
, равен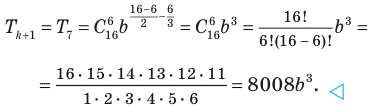
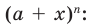
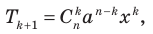
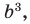 и записать его. Чтобы упростить запись общего члена разложения, запишем:
и записать его. Чтобы упростить запись общего члена разложения, запишем:
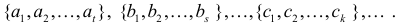
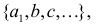 взяв из каждого исходного множества по одному элементу? Ответ на этот вопрос дают следующие рассуждения.
взяв из каждого исходного множества по одному элементу? Ответ на этот вопрос дают следующие рассуждения.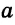 из первого множества можно выбрать
из первого множества можно выбрать 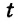 способами, элемент
способами, элемент 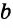 из второго – s способами, элемент с можно выбрать
из второго – s способами, элемент с можно выбрать  способами и т. д. Пару элементов
способами и т. д. Пару элементов 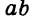 можно составить
можно составить 

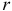 элементов («выборкой объема
элементов («выборкой объема 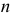 элементов (элементов «генеральной совокупности»). Различают два способа выбора:
элементов (элементов «генеральной совокупности»). Различают два способа выбора: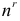 способами. Например, повторную выборку объема 2 из трех элементов
способами. Например, повторную выборку объема 2 из трех элементов 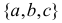 можно сделать 32 =9 способами:
можно сделать 32 =9 способами: 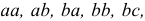
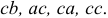
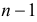 возможность выбора, третий элемент можно выбрать
возможность выбора, третий элемент можно выбрать 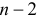 способами и т.д. Элемент выборки с номером
способами и т.д. Элемент выборки с номером 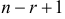 способом. Согласно комбинаторному принципу, общее число бесповторных выборок объема
способом. Согласно комбинаторному принципу, общее число бесповторных выборок объема 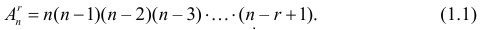
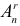 называют числом размещений из
называют числом размещений из 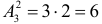 размещений из трех элементов
размещений из трех элементов 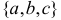 по два:
по два: 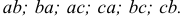 Отметим, что и в первом случае и во втором выборки отличаются либо составом элементов, либо порядком выбора элементов.
Отметим, что и в первом случае и во втором выборки отличаются либо составом элементов, либо порядком выбора элементов.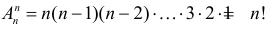
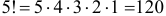 способами. Три элемента
способами. Три элемента 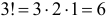 способами:
способами: 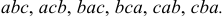
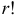 способами. Тогда
способами. Тогда 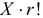 равно числу способов выбрать
равно числу способов выбрать 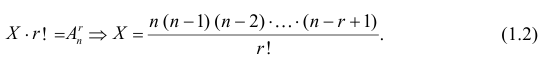
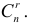 Если в формуле (1.2) умножить числитель и знаменатель на
Если в формуле (1.2) умножить числитель и знаменатель на 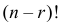 , то
, то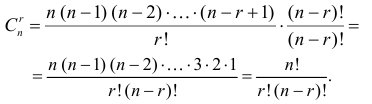
 по два существует
по два существует  . Это
. Это 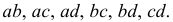
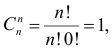 откуда следует, что
откуда следует, что 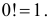
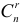 называют биномиальными коэффициентами. Название связано с формулой бинома Ньютона
называют биномиальными коэффициентами. Название связано с формулой бинома Ньютона
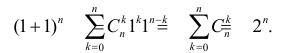

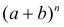 по формуле (1.3). Треугольником удобно пользоваться для нахождения значений
по формуле (1.3). Треугольником удобно пользоваться для нахождения значений 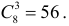
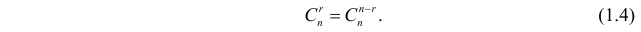
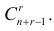 Еще раз подчеркнем, что речь идет о выборках, которые отличаются хотя бы одним элементом, а порядок выбора этих элементов во внимание не принимается. Число таких выборок можно подсчитать следующим образом. Между элементами
Еще раз подчеркнем, что речь идет о выборках, которые отличаются хотя бы одним элементом, а порядок выбора этих элементов во внимание не принимается. Число таких выборок можно подсчитать следующим образом. Между элементами 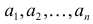 поставим разграничительные знаки, например, нули:
поставим разграничительные знаки, например, нули: 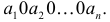 Таких знаков (нулей) понадобится
Таких знаков (нулей) понадобится 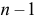 . На месте каждого элемента поставим столько единиц, сколько раз предполагается выбрать этот элемент. Например, комбинация
. На месте каждого элемента поставим столько единиц, сколько раз предполагается выбрать этот элемент. Например, комбинация 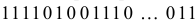 означает, что элемент
означает, что элемент 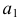 выбран четыре раза, элемент
выбран четыре раза, элемент 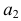 выбран один раз, элемент
выбран один раз, элемент 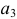 не выбран,..., элемент
не выбран,..., элемент 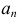 выбран два раза. Заметим, что в такой записи число единиц равно объему выборки
выбран два раза. Заметим, что в такой записи число единиц равно объему выборки 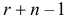 мест выбрать
мест выбрать 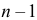 место и поставить на них нули, а на остальных местах разместить единицы. Это можно сделать способами.
место и поставить на них нули, а на остальных местах разместить единицы. Это можно сделать способами.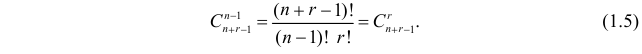
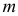 групп по
групп по 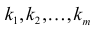 элементов соответственно
элементов соответственно 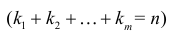 можно
можно 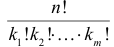 способами. Порядок элементов внутри каждой из этих
способами. Порядок элементов внутри каждой из этих 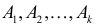 – множества, число элементов в каждом из которых равно соответственно
– множества, число элементов в каждом из которых равно соответственно 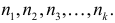 Составить множество B из
Составить множество B из  элементов множества А1,
элементов множества А1, 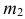 элементов множества А2, …,
элементов множества А2, …, 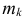 элементов множества Аk, можно, согласно основному комбинаторному принципу, способами.
элементов множества Аk, можно, согласно основному комбинаторному принципу, способами.