
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Перестановкой из n элементов называется любое упорядоченное множество из n данных элементов.Стр 1 из 13Следующая ⇒
Перестановкой из n элементов называется любое упорядоченное множество из n данных элементов. Иными словами, это такое множество, для которого указано, какой элемент находится на первом месте, какой — на втором,..., какой — на n-м. Формула числа перестановок
Пример: Количество различных шестизначных чисел, которые можно составить из цифр 1, 2, 3, 4, 5, 6, не повторяя эти цифры в одном числе, равно Размещения: Размещением из n элементов по k называется любое упорядоченное множество из k элементов, состоящее из элементов данного n-элементного множества. Формулы для нахождения количества соединений с повторениями обязательны только для классов физико-математического профиля. Формула числа размещений
Пример: Количество различных трехзначных чисел, которые можно составить из цифр 1, 2, 3, 4, 5, 6, если цифры не могут повторяться, равно
Сочетания: Всё о комбинаторике Пусть имеется несколько множеств элементов:
Вопрос: сколькими способами можно составить новое множество Элемент
Способы выбора трех элементов аbc перечислены в табл. 1.2.
В этой таблице Основной комбинаторный принцип. Если некоторый первый выбор можно сделать Комбинаторные формулы в прикладных задачах теории вероятностей обычно связывают с выбором
При повторном выборе каждый по порядку элемент может быть выбран
В случае бесповторной выборки первый элемент можно выбрать
Число Например, существует Выделим особо случай, когда один за другим выбраны все
называют числом перестановок из Например, пять человек могут встать в очередь Подсчитаем количество бесповторных выборок объема
Это число называют числом сочетаний из
Например, сочетаний из четырех элементов Так как из Величины
Из формулы (1.3) следует, что
Биномиальные коэффициенты образуют так называемый треугольник Паскаля, который имеет вид:
В Биномиальные коэффициенты обладают свойством симметрии:
Это наглядно демонстрирует треугольник Паскаля. Равенство (1.4) подтверждает тот очевидный факт, что выбор При повторном выборе из
Совокупность из Пусть
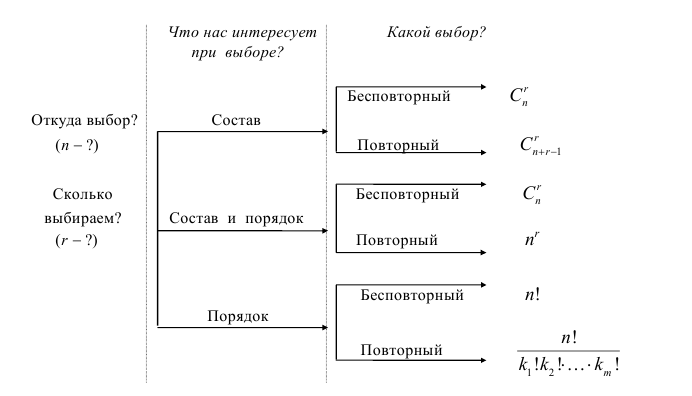
Для безошибочного выбора комбинаторной формулы достаточно последовательно ответить на вопросы в следующей схеме:
Например, число словарей, необходимых для непосредственного перевода с одного на другой, для пяти языков определяется из следующих рассуждений. Для составления словаря выбираем из пяти языков ( Пример №1 Сколькими способами можно выбрать путь из начала координат 0(0,0) в точку В(6,4), если каждый шаг равен единице, но его можно совершать только вправо или вверх? Сколько таких путей проходит через точку А(2,3)? Решение. Весь путь занимает 10 шагов (четыре вверх и шесть вправо). Для планирования пути следует решить, какие именно по счету четыре шага следует сделать вверх, а остальные шесть — вправо. Выбор бесповторный и нас интересует только состав выбора. Поэтому в описанных условиях всего путей из точки О в точку В будет Рассуждая подобным образом легко видеть, что путей из точки О в точку А существует Ответ. 210; 50. Пример №2 Сколькими способами можно выбрать путь из начала координат 0(0,0) в точку
Исходные данные к задаче 1.1.
Пример №3 В городе с идеальной прямоугольной планировкой (сеть улиц в этом городе изображена на рис. 1.1) из пункта А выходят
Решение. Каждый человек пройдет N улиц и окажется на одном из перекрестков На каждом перекрестке для каждого человека производится выбор из двух возможностей: идти в направлении В пункте Ответ. Пример №4 Сколькими способами можно Решение. Поставим эти предметы в ряд. Между ними будет Ответ. Пример 1.4. Сколькими способами можно распределить 6 яблок, 8 груш и 10 слив между тремя детьми? Сколькими способами это можно сделать так, чтобы каждый ребенок получил по меньшей мере одно яблоко, одну сливу и одну грушу? Решение. Яблоки в соответствии с формулой (1.5) можно распределить
Ответ. 83160; 7560. Пример №5 Сколько цифр в первой тысяче не содержат в своей записи цифры 5? Решение. Для записи любой из цифр 000, 001, 002,..., 999 необходимо трижды выбрать повторным способом одну из десяти цифр, поэтому и получается всего Ответ. 729. Пример №6 Сколько шестизначных чисел содержат в записи ровно три различных цифры? Решение. Заметим, что всего шестизначных чисел имеется Выбрать три ненулевых цифры можно Учтем теперь возможность использования нуля. К нулю нужно добавить две цифры, что можно сделать Ответ. 58320. Пример №7 В саду есть цветы десяти наименований (розы, флоксы, ромашки и т. д.). а) Сколькими способами можно составить букет из пяти цветков (не принимая во внимание совместимость растений и художественные соображения)? б) Сколькими способами можно составить букет из пяти различных цветков? в) Сколькими способами можно составить букет из пяти цветков так, чтобы в букете непременно было хотя бы по одному цветку двух определенных наименований Решение. а) Если запрета на повторение цветков нет, то мы имеем дело с повторным выбором и нас интересует только состав. Поэтому по формуле (1.5) получаем б) Если цветы должны быть разными, то способ выбора бесповторный и букет можно составить в) Отберем по одному цветку каждого из двух названных наименований. Три остальных цветка можно выбрать из 10 возможных Ответ. а) 2002; б) 504; в) 220. Пример №8 Имеется Решение. Ясно, что яблоки можно разложить
При ответе на второй вопрос учтем, что следует по одному яблоку сразу положить в каждую из корзин, а остальные Ответ. Пример №9 Требуется найти число натуральных делителей натурального числа Решение. Разложим
где Заметим, что при разделении числа
Так что разложение Ответ. Пример №10 Сколькими способами легкоатлет, собираясь на тренировку, может выбрать себе пару спортивной обуви, имея 5 пар кроссовок и 2 нары кед? Очевидно, что выбрать одну из имеющихся пар обуви, кроссовки или кеды, можно 5 + 2 = 7 способами. Обобщая, приходим к комбинаторному правилу сложения:
Это правило справедливо также для трех и более элементов. Пример №11 В меню школьной столовой предлагается на выбор 4 вида пирожков и 3 вида сока. Сколько разных вариантов выбора завтрака, состоящего из одного пирожка и одного стакана сока, имеется у учащегося этой школы? Пирожок можно выбрать 4 способами и к каждому пирожку выбрать сок 3 способами (рис. 76). Следовательно, учащийся имеет Обобщая, приходим к комбинаторному правилу умножения:
Это правило справедливо также для трех и более элементов. Пример №12 Сколько трехзначных чисел можно составить из цифр 1, 2, 3, 4, если в числе: 1) цифры не повторяются; 2) цифры могут повторяться?
Решение: 1) Первую цифру можем выбрать 4 способами (рис.77). Так как после выбора первой цифры их останется три (ведь цифры в нашем случае повторяться не могут), то вторую цифру можем выбрать 3 способами.И наконец, третью цифру можем выбрать из оставшихся двух - то есть 2 способами. Следовательно, количество искомых трехзначных у чисел будет равно 2) Применим комбинаторное правило умножения. Так как цифры в числе могут повторяться, то каждую из цифр искомого числа можно выбрать 4 способами (рис. 78), и тогда таких чисел будет Ответ. 1) 24 числа; 2) 64 числа. Отметим, что решить подобные задачи без применения комбинаторного правила умножения можно только путем перебора всех возможных вариантов чисел, удовлетворяющих условию задачи. Но такой способ решения является слишком долгим и громоздким. Пример №13 Сколько четных пятизначных чисел можно составить из цифр 5, 6, 7, 8, 9, если цифры в числе не повторяются? Решение: Четное пятизначное число можно получить, если последней его цифрой будет 6 или 8. Чисел, у которых последней является цифра 6, будет
а тех, у которых последней является цифра 8, - также 24. По комбинаторному правилу сложения всего четных чисел будет Ответ. 48. Пример №14 Азбука племени АБАБ содержит всего две буквы - «а» и «б». Сколько слов в языке этого племени состоит: 1) из двух букв; 2) из трех букв? Решение: 1) аа, ба, аб, бб (всего четыре слова); 2) ааа, ааб, аба, абб, ббб, бба, баб, баа (всего восемь слов). Заметим, что найденное количество слов соответствует комбинаторному правилу умножения. Так как на каждое место есть два «претендента» - «а» и «б», то слов, состоящих из двух букв, будет Пример №15 В футбольной команде из 11 игроков надо выбрать капитана и его заместителя. Сколькими способами это можно сделать? Решение: Капитаном можно выбрать любого из 11 игроков, а его заместителем - любого из 10 оставшихся игроков. Таким образом (по правилу умножения), имеем Пример №16 В Стране Чудес 10 городов и каждые два из них соединяет авиалиния. Сколько авиалиний в этой стране? Решение. Так как каждая авиалиния соединяет два города, то одним из них может быть любой из 10 городов, а другим - любой из 9 оставшихся. Следовательно, количество авиалиний равно Комбинаторные задачи неразрывно связаны с задачами теории вероятностей, еще одного раздела математики. В ХIII-ХII в. до н. э. встречаются упоминания о вопросах, близких к комбинаторным. Некоторые комбинаторные задачи решали и в Древней Греции. В частности, Аристоксен из Тарента (IV в. до н. э.), ученик Аристотеля, перечислил различные комбинации длинных и коротких слогов в стихотворных размерах. А Папп Александрийский в IV в. н. э. рассматривал число пар и троек, которые можно получить из трех элементов, допуская их повторения. Некоторые элементы комбинаторики были известны и в Индии во II в. до н. э. Индийцы умели вычислять числа, известные нам как коэффициенты формулы бинома Ньютона. Позднее, в VIII в. н. э., арабы нашли и саму эту формулу, и ее коэффициенты, которые сейчас вычисляют с помощью комбинаторных формул или «треугольника Паскаля». Свой нынешний вид упомянутые комбинаторные формулы приобрели благодаря средневековому ученому Леви бен Гершону (XIV в.) и французскому математику П. Эригону (XVII в.). В III в. н. э. сирийский философ Порфирий для классификации понятий составил специальную схему, получившую название «древо Порфирия». Сейчас подобные деревья используются для решения определенных задач комбинаторики в разнообразных областях знаний. Некоторые ранее неизвестные комбинаторные задачи рассмотрел Леонардо Пизанский (Фибоначчи) в своей знаменитой «Книге абака» (1202 г.), в частности, о нахождении наименьшего набора различных гирь, позволяющего взвесить груз с любой целочисленной массой, не превышающей заданного числа. Со времен греческих математиков были известны две последовательности, каждый член которых получали по определенному правилу из предыдущих, - арифметическая и геометрическая прогрессии. А Фибоначчи впервые в одной из задач выразил член последовательности через два предыдущих, используя формулу, которую назвали рекуррентной. В дальнейшем метод рекуррентных формул стал одним из мощнейших для решения комбинаторных задач. Как ни странно, развитию комбинаторики в значительной степени способствовали азартные игры, которые были очень популярны в XVI в. В частности, вопросами определения разнообразных комбинаций в игре в кости в то время занимались такие известные итальянские математики, как Д. Кардано, H. Тарталья и др. А наиболее полно изучил этот вопрос в XVII в. Галилео Галилей. Современные комбинаторные задачи высокого уровня сложности связаны с объектами в других отраслях математики: определителями, конечными геометриями, группами, математической логикой и т. п. Пример №17 В городе Решение: Обозначим буквой Описанную ситуацию можно обобщить в виде утверждения, которое называется правилом суммы. Если элемент некоторого множества Правило суммы распространяется и на большее количество множеств. Пример №18 Планируя летний отдых, семья определилась с местами его проведения: в Одессе — 1, в Евпатории — 3, в Ялте — 2, в Феодосии — 2. Сколько возможностей выбора летнего отдыха имеет семья? Решение: Поскольку все базы отдыха разные, то для решения задачи достаточно найти сумму элементов всех множеств, о которых говорится: Пример №19 От пункта Решение: Чтобы пройти от пункта Обобщим описанную ситуацию. Если первый компонент пары можно выбрать Это — правило произведения, его часто называют основным правилом комбинаторики. Обратите внимание: речь идёт об упорядоченных парах, составленных из различных компонентов. Правило произведения распространяется и на упорядоченные тройки, четвёрки и любые другие упорядоченные конечные множества. В частности, если первый компонент упорядоченной тройки можно выбрать
Описанной ситуации соответствует диаграмма, изображённая на рисунке 137. Такие диаграммы называют деревьями. Пример №20 Сколько разных поездов можно составить из 6 вагонов, если каждый из вагонов можно поставить на любом месте? Решение:
|
|||||||||
|
Последнее изменение этой страницы: 2022-01-22; просмотров: 92; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.86.134 (0.142 с.) |
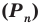

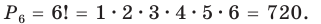
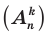
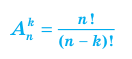
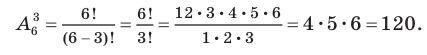
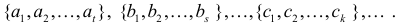
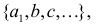 взяв из каждого исходного множества по одному элементу? Ответ на этот вопрос дают следующие рассуждения.
взяв из каждого исходного множества по одному элементу? Ответ на этот вопрос дают следующие рассуждения.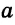 из первого множества можно выбрать
из первого множества можно выбрать 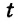 способами, элемент
способами, элемент 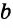 из второго – s способами, элемент с можно выбрать
из второго – s способами, элемент с можно выбрать  способами и т. д. Пару элементов
способами и т. д. Пару элементов 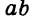 можно составить
можно составить 

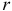 элементов («выборкой объема
элементов («выборкой объема 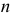 элементов (элементов «генеральной совокупности»). Различают два способа выбора:
элементов (элементов «генеральной совокупности»). Различают два способа выбора: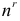 способами. Например, повторную выборку объема 2 из трех элементов
способами. Например, повторную выборку объема 2 из трех элементов 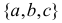 можно сделать 32 =9 способами:
можно сделать 32 =9 способами: 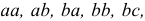
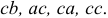
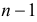 возможность выбора, третий элемент можно выбрать
возможность выбора, третий элемент можно выбрать 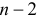 способами и т.д. Элемент выборки с номером
способами и т.д. Элемент выборки с номером 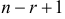 способом. Согласно комбинаторному принципу, общее число бесповторных выборок объема
способом. Согласно комбинаторному принципу, общее число бесповторных выборок объема 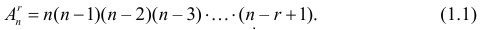
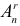 называют числом размещений из
называют числом размещений из 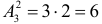 размещений из трех элементов
размещений из трех элементов 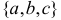 по два:
по два: 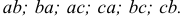 Отметим, что и в первом случае и во втором выборки отличаются либо составом элементов, либо порядком выбора элементов.
Отметим, что и в первом случае и во втором выборки отличаются либо составом элементов, либо порядком выбора элементов.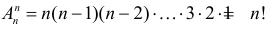
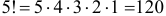 способами. Три элемента
способами. Три элемента 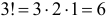 способами:
способами: 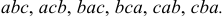
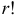 способами. Тогда
способами. Тогда 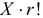 равно числу способов выбрать
равно числу способов выбрать 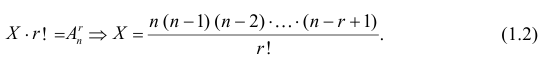
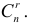 Если в формуле (1.2) умножить числитель и знаменатель на
Если в формуле (1.2) умножить числитель и знаменатель на 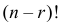 , то
, то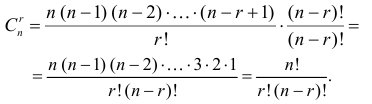
 по два существует
по два существует  . Это
. Это 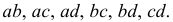
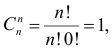 откуда следует, что
откуда следует, что 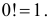
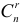 называют биномиальными коэффициентами. Название связано с формулой бинома Ньютона
называют биномиальными коэффициентами. Название связано с формулой бинома Ньютона
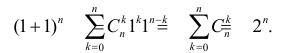

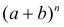 по формуле (1.3). Треугольником удобно пользоваться для нахождения значений
по формуле (1.3). Треугольником удобно пользоваться для нахождения значений 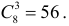
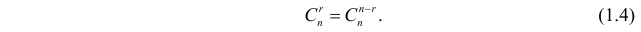
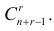 Еще раз подчеркнем, что речь идет о выборках, которые отличаются хотя бы одним элементом, а порядок выбора этих элементов во внимание не принимается. Число таких выборок можно подсчитать следующим образом. Между элементами
Еще раз подчеркнем, что речь идет о выборках, которые отличаются хотя бы одним элементом, а порядок выбора этих элементов во внимание не принимается. Число таких выборок можно подсчитать следующим образом. Между элементами 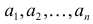 поставим разграничительные знаки, например, нули:
поставим разграничительные знаки, например, нули: 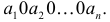 Таких знаков (нулей) понадобится
Таких знаков (нулей) понадобится 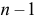 . На месте каждого элемента поставим столько единиц, сколько раз предполагается выбрать этот элемент. Например, комбинация
. На месте каждого элемента поставим столько единиц, сколько раз предполагается выбрать этот элемент. Например, комбинация 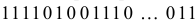 означает, что элемент
означает, что элемент 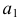 выбран четыре раза, элемент
выбран четыре раза, элемент 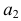 выбран один раз, элемент
выбран один раз, элемент 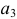 не выбран,..., элемент
не выбран,..., элемент 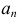 выбран два раза. Заметим, что в такой записи число единиц равно объему выборки
выбран два раза. Заметим, что в такой записи число единиц равно объему выборки 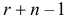 мест выбрать
мест выбрать 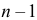 место и поставить на них нули, а на остальных местах разместить единицы. Это можно сделать способами.
место и поставить на них нули, а на остальных местах разместить единицы. Это можно сделать способами.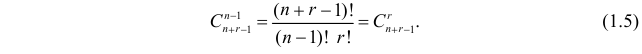
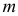 групп по
групп по 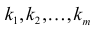 элементов соответственно
элементов соответственно 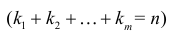 можно
можно 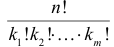 способами. Порядок элементов внутри каждой из этих
способами. Порядок элементов внутри каждой из этих 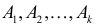 – множества, число элементов в каждом из которых равно соответственно
– множества, число элементов в каждом из которых равно соответственно 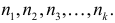 Составить множество B из
Составить множество B из  элементов множества А1,
элементов множества А1, 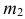 элементов множества А2, …,
элементов множества А2, …, 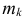 элементов множества Аk, можно, согласно основному комбинаторному принципу, способами.
элементов множества Аk, можно, согласно основному комбинаторному принципу, способами.
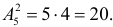
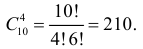
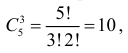 а путь из точки А в точку В можно выбрать
а путь из точки А в точку В можно выбрать 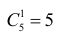 способами. По комбинаторному принципу всего путей через точку А существует 10 • 5 = 50.
способами. По комбинаторному принципу всего путей через точку А существует 10 • 5 = 50.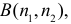 если каждый шаг равен 1, но его можно совершать только вправо или вверх? Сколько таких путей проходит через точку
если каждый шаг равен 1, но его можно совершать только вправо или вверх? Сколько таких путей проходит через точку 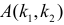 (См. пример 1.1 и исходные данные.)
(См. пример 1.1 и исходные данные.)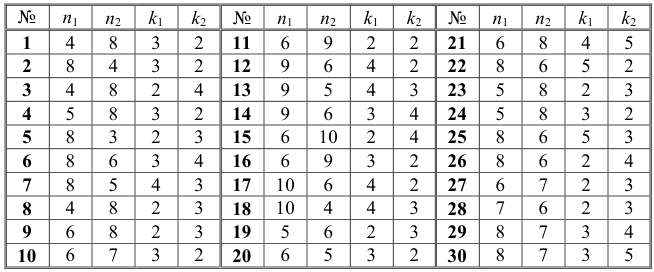
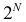 человек. Половина из них идет по направлению
человек. Половина из них идет по направлению 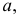 половина — по направлению
половина — по направлению  Дойдя до первого перекрестка, каждая группа разделяется так, что половина ее идет по направлению
Дойдя до первого перекрестка, каждая группа разделяется так, что половина ее идет по направлению 
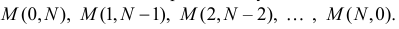 Координаты перекрестков указаны в предположении, что точка А служит началом координат.
Координаты перекрестков указаны в предположении, что точка А служит началом координат.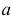 или в направлении
или в направлении 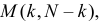 окажется столько человек, сколько различных путей ведет в этот пункт из точки А. Чтобы попасть в пункт
окажется столько человек, сколько различных путей ведет в этот пункт из точки А. Чтобы попасть в пункт 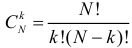 способами.
способами.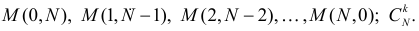
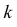 лицами так, чтобы каждый получил не менее одного предмета?
лицами так, чтобы каждый получил не менее одного предмета?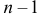 промежуток. В любые
промежуток. В любые 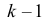 из этих промежутков поставим разделяющие перегородки. Тогда все предметы разделятся на
из этих промежутков поставим разделяющие перегородки. Тогда все предметы разделятся на 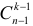 способами. Заметим, что вообще
способами. Заметим, что вообще 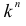 способами.
способами.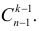
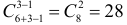 способами, груши —
способами, груши — 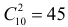 , а сливы
, а сливы 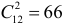 способами. По комбинаторному принципу всего способов
способами. По комбинаторному принципу всего способов 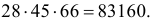 Если необходимо, чтобы каждый ребенок получил по меньшей мере одно яблоко, одну грушу и одну сливу, то в соответствии с формулой предыдущего примера имеем
Если необходимо, чтобы каждый ребенок получил по меньшей мере одно яблоко, одну грушу и одну сливу, то в соответствии с формулой предыдущего примера имеем 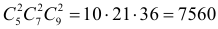 способов.
способов.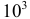 чисел. Если цифру 5 исключить, то выбор можно производить только из девяти цифр: 0, 1,2, 3, 4, 6, 7, 8, 9. Поэтому всего получится
чисел. Если цифру 5 исключить, то выбор можно производить только из девяти цифр: 0, 1,2, 3, 4, 6, 7, 8, 9. Поэтому всего получится  чисел в первой тысяче, в записи которых нет цифры 5.
чисел в первой тысяче, в записи которых нет цифры 5.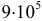 , так как первая цифра может быть любой (исключая нуль), а остальные пять могут быть выбраны
, так как первая цифра может быть любой (исключая нуль), а остальные пять могут быть выбраны 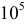 способами.
способами.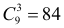 способами. Из выбранных трех цифр можно составить
способами. Из выбранных трех цифр можно составить 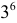 шестизначных чисел, из двух —
шестизначных чисел, из двух — 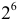 , а из одной —
, а из одной — 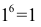 шестизначное число. По формуле (1.7) получаем, что существует
шестизначное число. По формуле (1.7) получаем, что существует 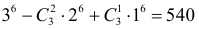 шестизначных чисел, в записи которых есть только три заданные цифры. Поэтому общее число шестизначных чисел, в записи которых имеются три отличные от нуля цифры, равно
шестизначных чисел, в записи которых есть только три заданные цифры. Поэтому общее число шестизначных чисел, в записи которых имеются три отличные от нуля цифры, равно 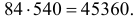
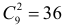 способами. Если, например, были выбраны цифры 0, 2, 5, то первой цифрой должна быть 2 или 5. К этой первой цифре в соответствии с формулой (1.7) можно добавить
способами. Если, например, были выбраны цифры 0, 2, 5, то первой цифрой должна быть 2 или 5. К этой первой цифре в соответствии с формулой (1.7) можно добавить 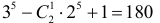 комбинаций остальных пяти цифр. Тогда всего шестизначных чисел, состоящих из 0, 2, 5 будет
комбинаций остальных пяти цифр. Тогда всего шестизначных чисел, состоящих из 0, 2, 5 будет 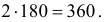 Всего же шестизначных чисел, записанных тремя цифрами, среди которых встречается нуль, ровно
Всего же шестизначных чисел, записанных тремя цифрами, среди которых встречается нуль, ровно 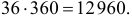 Всего чисел, удовлетворяющих условиям задачи, имеется
Всего чисел, удовлетворяющих условиям задачи, имеется 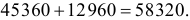
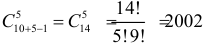 способа.
способа.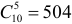 способами.
способами.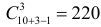 способами.
способами. яблок,
яблок,  груш и
груш и 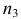 персиков. Сколькими способами можно их разложить по двум корзинам? Сколькими способами можно это сделать, если в каждой корзине должно быть хотя бы по одному фрукту всех названных видов (полагаем, что фруктов каждого наименования два или больше)?
персиков. Сколькими способами можно их разложить по двум корзинам? Сколькими способами можно это сделать, если в каждой корзине должно быть хотя бы по одному фрукту всех названных видов (полагаем, что фруктов каждого наименования два или больше)?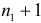 способом (в первую корзину можно не положить яблок совсем, положить одно яблоко, два яблока, …, все яблоки). Те же рассуждения в отношении груш и персиков дают соответственно
способом (в первую корзину можно не положить яблок совсем, положить одно яблоко, два яблока, …, все яблоки). Те же рассуждения в отношении груш и персиков дают соответственно 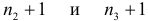 комбинаций. По комбинаторному принципу всего будет
комбинаций. По комбинаторному принципу всего будет 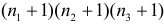 способов.
способов.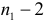 яблока раскладывать произвольным образом (в первую корзину либо не добавляем яблок, либо добавляем одно, либо –– два, …, либо – все
яблока раскладывать произвольным образом (в первую корзину либо не добавляем яблок, либо добавляем одно, либо –– два, …, либо – все 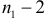 яблока). Все это можно сделать
яблока). Все это можно сделать 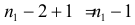 способами. Те же рассуждения насчет других фруктов и комбинаторный принцип дают следующий результат:
способами. Те же рассуждения насчет других фруктов и комбинаторный принцип дают следующий результат: 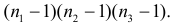
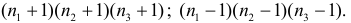
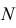 .
.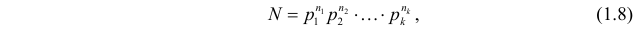
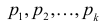 – различные простые числа. (Например,
– различные простые числа. (Например, 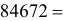
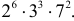 )
)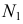 и
и  простые сомножители распределятся между
простые сомножители распределятся между  в число
в число 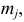 то разложение (1.8) примет вид:
то разложение (1.8) примет вид: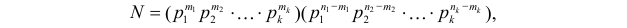
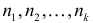 на две части, а это можно сделать
на две части, а это можно сделать 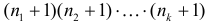 способами.
способами.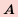 можно выбрать
можно выбрать 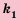 способами, а элемент
способами, а элемент 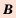 (независимо от выбора элемента
(независимо от выбора элемента 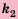 способами, то выбрать
способами, то выбрать 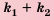 способами.
способами. 
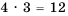 вариантов выбора завтрака.
вариантов выбора завтрака.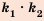 способами.
способами. 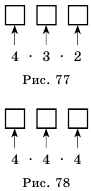
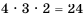 .
.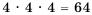 .
.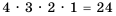 (рис. 79),
(рис. 79),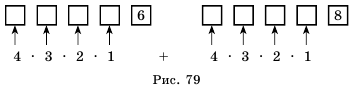
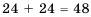 .
.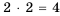 , а из трех букв -
, а из трех букв - 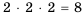 .
.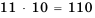 разных способов.
разных способов.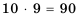 . Но при этом каждую из авиалиний мы учли дважды. Поэтому всего их будет
. Но при этом каждую из авиалиний мы учли дважды. Поэтому всего их будет 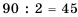 .
.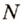 есть два университета — политехнический и экономический. Абитуриенту нравятся три факультета в политехническом университете и два — в экономическом. Сколько возможностей имеет студент для поступления в университет?
есть два университета — политехнический и экономический. Абитуриенту нравятся три факультета в политехническом университете и два — в экономическом. Сколько возможностей имеет студент для поступления в университет? множество факультетов, которые выбрал абитуриент в политехническом университете, а буквой
множество факультетов, которые выбрал абитуриент в политехническом университете, а буквой 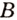 — в экономическом:
— в экономическом: 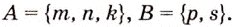 Поскольку эти множества не имеют общих элементов, то в делом абитуриент имеет
Поскольку эти множества не имеют общих элементов, то в делом абитуриент имеет 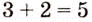 возможностей для поступления в университет.
возможностей для поступления в университет.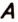 можно выбрать
можно выбрать  способами, а элемент множества
способами, а элемент множества 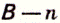 способами, то элемент из множества
способами, то элемент из множества 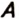 или из множества
или из множества 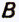 можно выбрать
можно выбрать  способами.
способами. Следовательно, семья может выбирать отдых из 8 возможных.
Следовательно, семья может выбирать отдых из 8 возможных.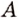 до пункта
до пункта 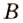 ведут три тропинки, а от
ведут три тропинки, а от 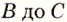 — две. Сколько маршрутов можно проложить от пункта
— две. Сколько маршрутов можно проложить от пункта 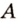 до пункта
до пункта 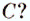
 до пункта
до пункта  надо выбрать одну из трёх тропинок: 1, 2 или 3 (рис. 136). После этого следует выбрать одну из двух других троп: 4 или 5. Всего от пункта
надо выбрать одну из трёх тропинок: 1, 2 или 3 (рис. 136). После этого следует выбрать одну из двух других троп: 4 или 5. Всего от пункта  до пункта
до пункта  ведут 6 маршрутов, потому что
ведут 6 маршрутов, потому что  Все эти маршруты можно обозначить с помощью пар:
Все эти маршруты можно обозначить с помощью пар: 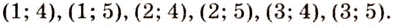
 способами, а. второй —
способами, а. второй — 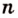 способами, то такую пару можно выбрать
способами, то такую пару можно выбрать  способами.
способами. способами, второй —
способами, второй — 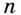 способами, третий —
способами, третий — 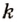 способами, то такую упорядоченную тройку можно выбрать
способами, то такую упорядоченную тройку можно выбрать 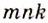 способами. Например, если столовая на обед приготовила 2 первых блюда — борщ (б) и суп (с), 3 вторых — котлеты (к), вареники (в), голубцы (г) и 2 десертных — пирожные (п) и мороженое (м), то всего из трёх блюд столовая может предложить 12 различных наборов, поскольку
способами. Например, если столовая на обед приготовила 2 первых блюда — борщ (б) и суп (с), 3 вторых — котлеты (к), вареники (в), голубцы (г) и 2 десертных — пирожные (п) и мороженое (м), то всего из трёх блюд столовая может предложить 12 различных наборов, поскольку 





