Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Правила техники безопасности при выполнении лабораторных работСодержание книги
Поиск на нашем сайте
ФИЗИКА лабораторный практикум для обучающихся по основной профессиональной образовательной программе высшего образования –программе специалитета по специальности 31.05.01 «Лечебное дело» Кемерово 2021 УДК 53(076.5) ББК 22.3я73 Ф 503
Физика: лабораторный практикум для обучающихся по основной профессиональной образовательной программе высшего образования –программе специалитета по специальности «Лечебное дело» / Е. В. Салтанова, О. В. Головко, Г.Н. Дадаева, Е.В. Просвиркина - Кемерово, 2021. – 91 с.
Лабораторный практикумразработан в соответствии с ФГОС ВО - специалитет по специальности 31.05.01 Лечебное дело, квалификация «врач-лечебник», утвержденным приказом Министерства науки и высшего образования Российской Федерации № 988 от «12» августа 2020 г. (рег. в Министерстве юстиции РФ № 59493 от 26 августа 2020 г.), а также в соответствии с рабочей программой дисциплины «Физика, математика». Лабораторный практикум содержит рекомендации к выполнению лабораторных работ, их содержание и критерии оценивания. Практикумпредназначен для обучающихся I–го курса обучающихся по программе специалитета по специальности «Лечебное дело» очной формы обучения.
Авторы: Салтанова Елена Владимировна – ст. преподаватель кафедры медицинской, биологической физики и высшей математики ФГБОУ ВО «Кемеровский государственный медицинский университет» Минздрава России. Головко Ольга Владимировна – доценткафедры медицинской, биологической физики и высшей математики ФГБОУ ВО «Кемеровский государственный медицинский университет» Минздрава России. Дадаева Галина Николаевна – ст. преподаватель кафедры медицинской, биологической физики и высшей математики ФГБОУ ВО «Кемеровский государственный медицинский университет» Минздрава России. Просвиркина Елена Владимировна –заведующий кафедрой медицинской, биологической физики и высшей математики ФГБОУ ВО «Кемеровский государственный медицинский университет» Минздрава России.
Рекомендовано на заседании кафедры медицинской, биологической физики и высшей математики, в качестве лабораторного практикума для обучающихся по основной профессиональной образовательной программе высшего образования –программе специалитета по специальности 31.05.01 «Лечебное дело» протокол №1 от 31.08.2021г.
©Ф ГБОУ ВО «Кемеровский государственный
СОДЕРЖАНИЕ Введение. 4 Рекомендации по подготовке и выполнению лабораторных работ. 5 Правила техники безопасности при выполнении лабораторных работ. 6 Критерии оценивания выполнения лабораторной работы и её защиты.. 6 Тема: Элементы механики твердого тела. 9 Тема: Гидродинамика. 16 Тема: Вопросы гемодинамики: особенности движения крови в кровеносной системе человека. 26 Тема: Энергетический баланс организма. 35 Тема: Механические колебания и волны. Акустика. 38 Тема: Электричество. 46 Тема: Геометрическая оптика. Рефрактометрия. 59 Тема: Микроскопия. Специальные приемы микроскопии. 72 Тема: Взаимодействие света с веществом. 82 Единицы измерения физических величин. 90 Множители и приставки для образования кратных и дольных единиц. 90 Греческий и Латинский алфавиты.. 91
Введение
Целью изучения физики в медицинском вузе является формирование у обучающихся представления о современной естественнонаучной картине мира и создании базы знаний для дальнейшего изучения профильных дисциплин и выработки умений использовать полученные знания в будущей профессиональной деятельности. Лабораторный практикум составлен в соответствии с ФГОС ВО - специалитет по специальности 31.05.01 Лечебное дело, квалификация «врач-лечебник», утвержденным приказом Министерства науки и высшего образования Российской Федерации № 988 от «12» августа 2020 г. (рег. в Министерстве юстиции РФ № 59493 от 26 августа 2020 г.) и в соответствии с рабочей программой дисциплины «Физика, математика». Цель практикума заключается в формировании компетенций - Системное и критическое мышление: УК 1 - Способен осуществлять критический анализ проблемных ситуаций на основе системного подхода, вырабатывать стратегию действий. ИД-1 УК-1 Уметь получать новые знания на основе анализа, синтеза и пр. Издание написано с целью организации аудиторной самостоятельной работы студентов при проведении лабораторного практикума. В первой части практикума излагаются рекомендации по подготовке и выполнению лабораторных работ и правила техники безопасности. Во второй части, являющейся основной, представлен разработанный лабораторный практикум, включающий описание лабораторных работ, по разделам «Элементы механики твердого тела», «Механика жидкости», «Энергетический баланс организма», «Механические колебания и волны. Акустика» «Электричество и магнетизм», «Оптика». Для каждой лабораторной работы приведены теоретические сведения, содержащие краткое изложение теоретического материала, порядок выполнения эксперимента, схемы (рисунки) приборов и установок, расчётные формулы. Рекомендации по подготовке и выполнению лабораторных работ
При внеаудиторной подготовке к лабораторным работам обучающийся должен: - подготовить устные ответы на контрольные вопросы, используя рекомендованную учебную, учебно-методическую литературу и конспект лекций. - изучить методические рекомендации по проведению лабораторной работы; - подготовить форму отчёта, включающую: · номер и наименование работы. · цель работы, · перечень оборудования, · схемы (рисунки) установки или прибора, · расчётные формулы с пояснением физических величин, · таблицы результатов измерений и вычислений (заполняется при выполнении работы); Во время лабораторного занятия обучающийся должен: 1. Изучить оборудование и собрать установку необходимую для проведения эксперимента. 2. Получить у преподавателя допуск к выполнению лабораторной работы. 3. Под руководством преподавателя или лаборанта провести экспериментальную часть работы. 4. В процессе выполнения работы записать в тетрадь экспериментальные данные. 5. Выполнить необходимые расчёты и вычислить погрешности измерений. 6. Построить графики с учётом масштаба. 7. Сделать выводы по результатам лабораторной работы. 8. В конце занятия подписать у преподавателя отчёт по работе.
Литература 1. Медицинская и биологическая физика [Электронный ресурс]: учебник / Ремизов А.Н. - 4-е изд., испр. и перераб. - М.: ГЭОТАР-Медиа, 2013. Глава 9, §9.1 – 9.5. 2. Ливенцев Н.М. Курс физики: учебник. – 7-е изд., стер. – СПб.: Лань, 2014, Глава 2, §6-8. 3. Физика и биофизика. Руководство к практическим занятиям [Электронный ресурс]: учебное пособие / Антонов В.Ф., Черныш А.М., Козлова Е.К., Коржуев А.В. - М.: ГЭОТАР-Медиа, 2013. Лабораторная работа 2.1. Теоретические сведения Знание механических свойств тканей организма и, в частности, костной ткани необходимо при изучении опорно-двигательного аппарата человека, в хирургии, ортопедии, травматологии, при подборе трансплантантов для костно-пластических и реконструктивных операций. Деформацией называют изменения взаимного положения точек тела под действием внешних сил. Деформация называется упругой,если после прекращения действия сил тело восстанавливает свою форму, в противном случае деформация называется пластической (остаточной). К основным видам деформаций относят деформации: 1. растяжения; 2. сжатия; 3. изгиба; 4. сдвига; 5. кручения (рис.1).
В теории упругости доказывается, что все виды деформации могут быть сведены к одновременно происходящим деформациям растяжения (сжатия) и сдвига. Количественной мерой, характеризующей степень деформации, является относительное удлинение
где Сила, действующая на единицу площади поперечного сечения, называется напряжением (механическим):
для упругих деформаций справедлив закон Гука, согласно которому механическое напряжение и относительная деформация прямо пропорциональны друг другу: где коэффициент пропорциональности Е называется модулем Юнга. Из (3) видно, что модуль Юнга численно равен механическому напряжению при ε =1. Модуль Юнга зависит от свойств материала, является характеристикой упругих свойств материала. В таблице 1 представлены значения модулей упругости (модуля Юнга) некоторых материалов.
Таблица 1
Зависимость механического напряжения от относительной деформации для твердых тел показана на рис. 2. Зависимость
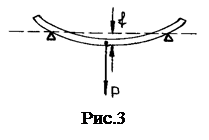
Кости характеризуются очень высокой механической прочностью. В зависимости от типа кости и ее участка механическое разрушение начинается по достижении напряжения 107-108 Существуют различные методы определения модуля упругости. Будем определять модуль упругости по деформации изгиба. Если к середине прямого упругого стержня, свободно лежащего на твердых опорах, приложена сила Р, то стержень изгибается (рис.3). Перемещение f,которое получает середина стержня, называется стрелой прогиба. Она зависит от нагрузки стержня и его модуля упругости. Для образца кости в форме трубки теория дает следующее выражение для модуля упругости:
где F – нагрузка, lср - длина образца (расстояние между опорами), aср, bср – ширина и высота образца соответственно, λ - стрела прогиба.
Задание 1. Исследование зависимости стрелы прогиба от величины нагрузки. ВНИМАНИЕ! С индикатором длины обращайтесь предельно аккуратно! Малейшее присутствие воды или масла на исследуемом изделии приводит к искажению показаний. Следите за тем, чтобы прямой и обратный ходы были плавными, без ударов в конце хода, т.к. это может привести к снятию и выкрашиванию зубьев механизма и увеличению погрешностей индикатора. Для исключения резких ударов в конце хода рекомендуется стержень придерживать рукой. 1. Образец располагается на опорах, как показано на рисунке 4. Крюк чашки для гирь устанавливают на середине образца.
Рис. 4
2. Измерительный стержень индикатора длины приводят в соприкосновение с верхней гранью в середине образца, устанавливают стрелку индикатора в нулевое положение поворотом шкалы. 3. Постепенно, без толчков нагружают чашку гирями, отмечая для каждого груза соответствующую стрелу прогиба по индикатору. Определение стрелы прогиба нужно производить только в области упругих деформаций. Результаты заносят в таблицу 2. Таблица 2
4. По найденным значениям стрелы прогиба и соответствующим нагрузкам постройте график. Для этого по оси абсцисс откладывают нагрузку, а по оси ординат – стрелу прогиба. 5. Сформулируйте вывод. Задание 2. Определение модуля упругости материалов. 1. При помощи штангенциркуля, микрометра и линейки измерьте длину Таблица 3
2. Найдите модуль упругости по формуле
где 3. Запишите физический смысл модуля упругости 4. Сформулируйте общий вывод.
Тема: Гидродинамика Цель работы 1. Изучить явление внутреннего трения в жидкостях. 2. Научиться определять коэффициент динамической вязкости жидкости методом Стокса. Оборудование 1. Цилиндрический сосуд с нанесённой масштабной шкалой, наполненный исследуемой жидкостью. 2. Шарик из материала известной плотности. 3. Секундомер. 4. Микрометр. Контрольные вопросы 1. Идеальная жидкость. Основные понятия течения идеальной жидкости. Уравнение неразрывности струи, следствие. Уравнение Бернулли. 2. Понятие ламинарного и турбулентного течения жидкости. Число Рейнольдса. 3. Явление внутреннего трения в жидкостях. Формула Ньютона. Коэффициент динамической вязкости: физический смысл, единицы измерения, зависимость от температуры. 4. Поперечный градиент скорости, единицы измерения, физический смысл. 5. Относительная вязкость жидкости, единицы измерения, физический смысл. 6. Кинематическая вязкость жидкости, единицы измерения, физический смысл 7. Течение жидкости по горизонтальной трубе постоянного сечения. Закон Пуазейля, формула Гагена- Пуазейля. 8. Определение динамической вязкости методом Стокса. Литература 4. Медицинская и биологическая физика [Электронный ресурс]: учебник / Ремизов А.Н. - 4-е изд., испр. и перераб. - М.: ГЭОТАР-Медиа, 2013. Глава 9, §9.1 – 9.5. 5. Ливенцев Н.М. Курс физики: учебник. – 7-е изд., стер. – СПб.: Лань, 2014, Глава 2, §6-8. 6. Физика и биофизика. Руководство к практическим занятиям [Электронный ресурс]: учебное пособие / Антонов В.Ф., Черныш А.М., Козлова Е.К., Коржуев А.В. - М.: ГЭОТАР-Медиа, 2013. Лабораторная работа 2.1. Теоретические сведения Живой организм - сложная система. Большую часть его составляют жидкие среды (кровь, лимфа, синовиальная, плевральная и др. жидкости), благодаря перемещению которых ткани и органы получают питательные вещества и осуществляется взаимодействие организма с окружающей средой. Одним из важных свойств жидкостей является вязкость или внутреннее трение. Определение вязкости имеет большое значение в практической медицине: · в клинической диагностике: измерение вязкости крови с помощью вискозиметров, оценка скорости оседания эритроцитов; · в судебной медицине (используют зависимость вязкости крови от возраста и пола); · в медицинских исследованиях: определяется вязкость (микровязкость) цитоплазмы клетки. Она зависит от структуры составляющих её биополимеров и субклеточных образований, от периода клеточного цикла, от температуры, от интенсивности различных внешних воздействий (например, радиоактивного облучения). Вязкость жидкости – это свойство реальной жидкости оказывать сопротивление перемещению одного слоя жидкости относительно другого. Вязкость проявляется в том, что при относительном перемещении слоёв жидкости с разными скоростями медленнее движущийся слой жидкости «тормозит» слой, движущийся быстрее, и наоборот. Вязкость обусловлена наличием между молекулами жидкости сил притяжения, которые при перемещении одного слоя жидкости относительно другого сдерживают движение слоёв. Вязкость или внутреннее трение зависит от вида течения жидкости. Различают два вида течения: ламинарное и турбулентное. Ламинарное течение - течение жидкости, при котором отдельные её слои движутся параллельно друг другу без завихрений и не перемешиваются. Турбулентным называют течение, при котором происходит интенсивное вихреобразование и перемешивание слоёв жидкости, при таком течении скорость частиц жидкости беспрерывно и хаотически изменяется. Ньютон установил, что при ламинарном течении, между слоями жидкости, движущимися с различными скоростями
Поперечный градиент скорости
В СИ единицей измерения поперечного градиента скорости является с-1. Физический смысл динамического коэффициента вязкости формулируется из формулы Ньютона (1): Согласно выражению (3) коэффициент динамической вязкости численно равен силе внутреннего трения, действующей между двумя слоями жидкости на площади соприкосновения 1 м2 при градиенте скорости, равном 1 с-1. В СИ единицей измерения коэффициента динамической вязкости является Па∙с (паскаль-секунда). На практике часто вязкость измеряют во внесистемных единицах - пуазах (Пз). Соотношение между Пуазом и Паскаль-секундой: 1 Па⋅с = 10 Пз. Для многих жидкостей коэффициент динамической вязкости зависит только от её химического состава (или природы жидкости) и температуры; с повышением температуры вязкость уменьшается. В некоторых случаях принято пользоваться кинематической вязкостью ( В СИ кинематическая вязкость измеряется в м2/с. Для характеристики вязкости на практике часто применяют понятие относительной вязкости здесь
Относительная вязкость показывает во сколько раз вязкость жидкости больше вязкости воды при одинаковых температурах. Относительная вязкость крови является важным диагностическим показателем состояния организма. Сила внутреннего трения или вязкость возникает не только при движении жидкости относительно покоящегося тела, но и при движении твёрдого тела в покоящейся жидкости. На этом основан метод измерения вязкости по Стоксу. Стокс опытным путём определил силу сопротивления, действующую на шарик, движущийся в жидкости: здесь
Формула (6) называется законом Стокса Для определения вязкости жидкости методом Стокса в стеклянный цилиндрический сосуд наливают исследуемую жидкость и наблюдают в ней свободное падение небольшого шарика. В этом случае при движении шарика играет роль не трение шарика о жидкость, а трение отдельных слоёв жидкости друг о друга: слой жидкости, примыкающий к шарику, прилипает к его поверхности вследствие межмолекулярного притяжения и движется вместе ним. Соседние слои жидкости так же вовлекаются в движение, которое носит ламинарный характер, но с меньшими скоростями. Метод Стокса применим при выполнении следующих условий: 1. жидкость должна представлять собой безграничную среду, т.е. диаметр шарика должен быть много меньше диаметра сосуда, в котором жидкость находится; 2. обтекание шарика жидкостью должно носить ламинарный характер, т.е. скорость движения шарика должна быть небольшой; 3. движение шарика в среде должно быть равномерным. Для достижения равномерного движения шарика необходимо, чтобы результирующая всех сил, действующих на него во время движения, была равна нулю. На шарик, движущийся в жидкости, действуют три силы (рисунок 6):
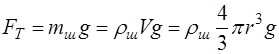 , (7) , (7)
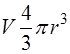 – объём шарика, – объём шарика,
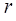 – радиус шарика, – радиус шарика,
Выталкивающая сила или сила Архимеда (
здесь
Сила сопротивления движению (согласно закону Стокса): Сила тяжести и выталкивающая сила постоянны. Сила сопротивления прямо пропорциональна скорости и поэтому на начальном этапе она меньше силы тяжести, и шарик падает ускоренно. При этом сила сопротивления увеличивается и наступает момент, когда все три силы уравновешиваются. Шарик начинает двигаться равномерно. В этом случае уравнение движения шарика в векторной форме примет вид: В скалярной форме уравнение движения в проекции на ось x (рисунок 6) имеет вид: С учётом (7), (8), (9) уравнение движения (11) примет вид:
Откуда
Если радиус шарика заменить на его диаметр: Таким образом, определение коэффициента динамической вязкости жидкости методом Стокса сводится к измерению диаметра шарика, расстоянию между метками и времени равномерного падения в жидкости между метками, плотности материала шарика и жидкости считаются известными. Задание 1. Определение коэффициента динамической вязкости жидкости методом Стокса 1. Запишите в таблицу 1 плотность исследуемой жидкости ( 2. Измерьте расстояние ( 3. Микрометром измерьте 3 раза диаметр шарика ( 4. Вычислите среднее значение диаметра шарика по формуле:
Результат запишите в таблицу 1. 5. Определите время равномерного падения шарика. Для этого опустите шарик как можно ближе к оси сосуда; расположите глаза на уровне верхнего кольца А (при этом кольцо должно слиться в прямую линию) и в момент прохождения шарика мимо кольца включите секундомер. К этому времени движение шарика будет равномерным. В момент прохождения шарика мимо нижнего кольца А1 выключите секундомер и запишите время t падения шарика. 6. Вычислите коэффициент динамической вязкости жидкости по формуле:
При вычислениях все величины должны быть в основных единицах системы СИ. 7. Рассчитайте относительную погрешность коэффициента динамической вязкости жидкости по формуле:
здесь
8. Вычислите абсолютную погрешность коэффициента динамической вязкости жидкости по формуле:
9. Результаты вычислений запишите в таблицу 1. 10. Запишите результат эксперимента с учётом погрешностей в виде:
11. Запишите физический смысл коэффициента динамической вязкости исследуемой жидкости. Задание 2. Вычисление относительной и кинематической вязкости Жидкости. 1. Вычислите относительную вязкость исследуемой жидкости 2. Вычислите кинематическую вязкость исследуемой жидкости 3. Результаты всех измерений и вычислений запишите в таблицу 1. Таблица 1.
4. Сделайте вывод по работе в соответствии с поставленными целями.
Тема: Вопросы гемодинамики: особенности движения крови в кровеносной системе человека.
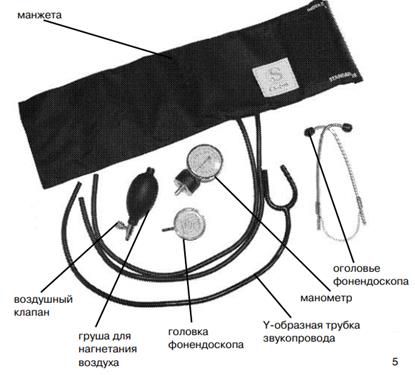
Цель: 1. изучить физические основы аускультационной и осциллометрической методики измерения артериального давления крови; 2. изучить принцип работы механического и электронного тонометров; 3. освоить навыки измерения артериального давления механическим и электронным тонометрами. Оборудование: 1. тренажер для обучения методике измерения артериального давления, 2. механический тонометр, 3. полуавтоматический тонометр, 4. автоматический тонометр, 5. запястный тонометр, 6. фонендоскоп, 7. спиртовые салфетки. Контрольные вопросы 1. Большой круг кровообращения. Модели кровообращения (модель Франка). 2. Непрерывность кровотока в кровеносной системе с физической точки зрения. 3. Изменение скорости кровотока в большом круге кровообращения. 4. Ламинарное и турбулентное течение крови. Число Рейнольдса. 5. Ударный объем крови. 6. Пульсовая волна: определение, уравнение. Изменение амплитуды пульсовой волны в зависимости от участка кровеносной системы. 7. Давление крови, систолическое и диастолическое давление, единицы измерения. 8. Изменение давления крови в большом круге кровообращения. 9. Прямые методы измерения давления крови. Принцип работы датчиков, применяемых в прямых методах измерения крови. 10. Физические основы измерения давления крови методом Короткова (аускультативная методика). 11. Объяснить, почему в методе Короткова давление воздуха в манжете можно считать равным давлению крови в артерии. 12. Методика измерения давления крови в артерии методом Короткова. 13. Физические основы измерения давления крови осциллометрическим методом. 14. Принцип работы датчиков, используемых в автоматических тонометрах (пьезоэлектрический, емкостной датчики). 15. Методика измерения давления крови электронным автоматическим тонометром. Литература 1. Ремизов, А. Н. Медицинская и биологическая физика: учебник / А.Н. Ремизов, [Электронный ресурс]- М.: ГЭОТАР-Медиа, 2013. – 647 с. – URL-: ЭБС «Консультант студента. Электронная библиотека медицинского вуза» www.studmedlib.ru 2. Ливенцев, Н.М. Курс физики: учебник для студентов вузов, обучающихся по техническим и технологическим направлениям / Н. М. Ливенцев. – 7-е изд., стер. – СПб: Лань, 2014. – 666 с, §143. Задание 1. Изучение конструкции и принципа действия механического тонометра. 1. По рисунку 7 изучите конструкцию механического тонометра.
Рисунок 7. Основные части механического тонометра 2. Покажите основные части механического тонометра на измерителе артериального давления модели CS-106. 3. Запишите принцип действия механического тонометра. Задание 2. Изучение методики измерения артериального давления механическим тонометром. 1. Наложите манжету на обнаженное плечо пациента на 2-3 см выше локтевого сгиба. Одежда не должна сдавливать плечо выше манжеты. 2. Закрепите манжету так, чтобы между ней и плечом проходил только один палец. 3. Соедините манометр с манжетой. Проверьте положение стрелки манометра относительно нулевой отметки шкалы. 4. Нащупайте пульс плечевой артерии в
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2022-01-22; просмотров: 94; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.227.250 (0.012 с.) |

 медицинский университет» Минздрава России, 2021
медицинский университет» Минздрава России, 2021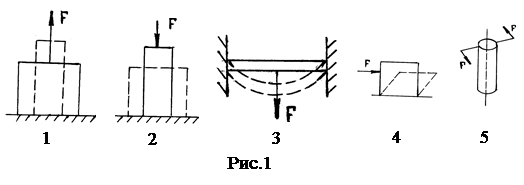
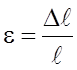 , (1)
, (1)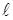 – начальная длина тела,
– начальная длина тела, 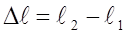 - изменение длины (абсолютное удлинение). При растяжении
- изменение длины (абсолютное удлинение). При растяжении 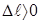 , при сжатии
, при сжатии 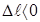 .
.
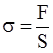 . (2)
. (2)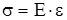 или
или 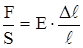 . (3)
. (3)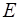 , Па
, Па
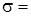 f(ε) для компактной костной ткани имеет аналогичный вид. При небольшом напряжении деформация носит упругий характер, что выражается на графике прямо пропорциональной зависимостью (участок ОВ).
f(ε) для компактной костной ткани имеет аналогичный вид. При небольшом напряжении деформация носит упругий характер, что выражается на графике прямо пропорциональной зависимостью (участок ОВ). 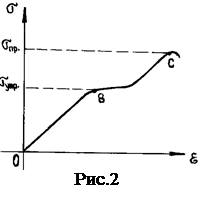 Наибольшее механическое напряжение σупр, при котором деформация сохраняет упругий характер, называется пределом упругости.При дальнейшем увеличении напряжения деформация имеет пластический характер (участок ВС) (рис.2), и при значении напряжения σпр происходит разрушение тела.
Наибольшее механическое напряжение σупр, при котором деформация сохраняет упругий характер, называется пределом упругости.При дальнейшем увеличении напряжения деформация имеет пластический характер (участок ВС) (рис.2), и при значении напряжения σпр происходит разрушение тела.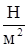 . В сравнении с костями прочность других биоматериалов низкая, так, например, ткань стенок крупных артерий выдерживает лишь напряжение ≈ 3∙106
. В сравнении с костями прочность других биоматериалов низкая, так, например, ткань стенок крупных артерий выдерживает лишь напряжение ≈ 3∙106 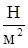 .
.
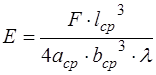 , (4)
, (4)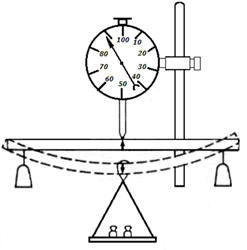
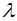 , мм
, мм
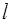 , ширину
, ширину 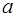 и высоту
и высоту 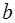 образца. Измерение каждой величины проделать три раза и найти среднее значение. Результаты занесите в таблицу 3.
образца. Измерение каждой величины проделать три раза и найти среднее значение. Результаты занесите в таблицу 3.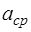 , м
, м
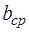 , м
, м
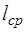 , м
, м
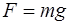 – деформирующая нагрузка,
– деформирующая нагрузка,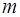 (кг) – масса гирьки;
(кг) – масса гирьки;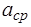 ,
, 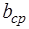 ,
, 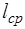 (м) – средние значения размеров образца.
(м) – средние значения размеров образца. 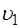 и
и 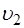 , возникают силы внутреннего трения, направленные по касательной к поверхности соприкосновения слоёв (рисунок 5). Модуль силы внутреннего трения (
, возникают силы внутреннего трения, направленные по касательной к поверхности соприкосновения слоёв (рисунок 5). Модуль силы внутреннего трения (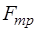 ) определяется по формуле Ньютона:
) определяется по формуле Ньютона: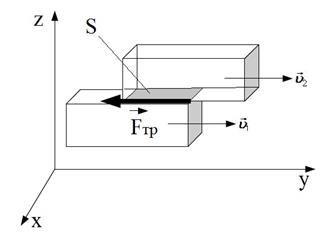
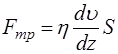 (1)
(1)
 здесь
здесь 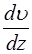 – поперечный градиент скорости
– поперечный градиент скорости 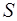 – площадь соприкосновения слоёв,
– площадь соприкосновения слоёв, 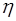 - коэффициент динамической вязкости (часто называют вязкостью).
- коэффициент динамической вязкости (часто называют вязкостью).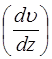 характеризует быстроту изменения скорости между двумя слоями жидкости и численно равен изменению скорости, приходящемуся на единицу расстояния между слоями в направлении, перпендикулярном поверхности слоя и определяется по формуле:
характеризует быстроту изменения скорости между двумя слоями жидкости и численно равен изменению скорости, приходящемуся на единицу расстояния между слоями в направлении, перпендикулярном поверхности слоя и определяется по формуле: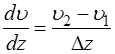 (2)
(2)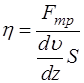 (3)
(3) ), равной коэффициенту динамической вязкости жидкости (
), равной коэффициенту динамической вязкости жидкости (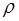 ):
):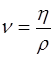 . (4)
. (4)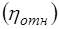 :
: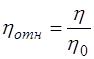 , (5)
, (5) Па⋅с – вязкость воды при 200 С.
Па⋅с – вязкость воды при 200 С. , (6)
, (6)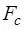 – сила сопротивления, она направлена в сторону, противоположную скорости и обусловлена внутренним трением или вязкостью жидкости.
– сила сопротивления, она направлена в сторону, противоположную скорости и обусловлена внутренним трением или вязкостью жидкости.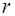 – радиус шарика,
– радиус шарика,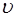 – скорость движения шарика.
– скорость движения шарика.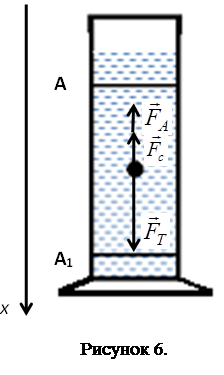 Сила тяжести (
Сила тяжести (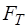 ):
):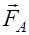
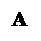 здесь
здесь 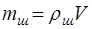 – масса шарика,
– масса шарика,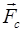
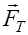
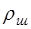 – плотность материала шарика,
– плотность материала шарика,
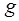 – ускорение свободного падения.
– ускорение свободного падения.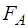 ):
):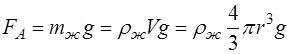 , (8)
, (8) 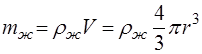 – масса вытесненной шариком жидкости,
– масса вытесненной шариком жидкости,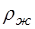 – плотность жидкости.
– плотность жидкости.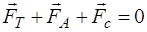 (10)
(10)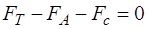 (11)
(11)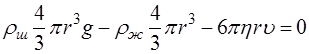 . (12)
. (12)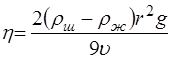 . (13)
. (13) , а скорость равномерного движения записать в виде:
, а скорость равномерного движения записать в виде: 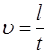 , здесь
, здесь 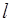 – расстояние между верхней (А) и нижней (А1) метками на сосуде с жидкостью (рисунок 6),
– расстояние между верхней (А) и нижней (А1) метками на сосуде с жидкостью (рисунок 6), 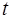 – время, за которое это расстояние пройдено, то коэффициент динамической вязкости жидкости можно определить по формуле:
– время, за которое это расстояние пройдено, то коэффициент динамической вязкости жидкости можно определить по формуле: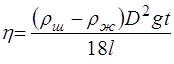 (14)
(14)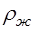 ) и плотность материала шарика (
) и плотность материала шарика (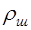 ).
).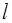 ) между метками А и А1, выполненных в виде колец, на сосуде, результат в таблицу 1.
) между метками А и А1, выполненных в виде колец, на сосуде, результат в таблицу 1.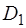 ,
, 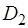 ,
, 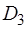 ).
).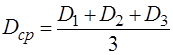 . (15)
. (15)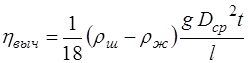 . (16)
. (16)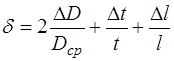 , (17)
, (17)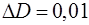 мм
мм 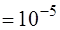 м – точность микрометра,
м – точность микрометра,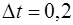 с – абсолютная погрешность секундомера,
с – абсолютная погрешность секундомера,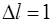 мм
мм 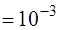 м – абсолютная погрешность измерения расстояния
м – абсолютная погрешность измерения расстояния 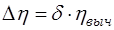 . (18)
. (18)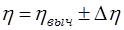 ,
, 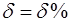 . (19)
. (19)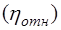 по формуле (5). Запишите физический смысл относительной вязкости исследуемой жидкости.
по формуле (5). Запишите физический смысл относительной вязкости исследуемой жидкости.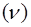 по формуле (4).
по формуле (4).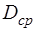 , м
, м
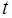 , с
, с
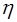 , Па∙с
, Па∙с
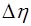 , Па∙с
, Па∙с
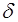 , %
, %
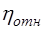
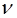 , м2/с
, м2/с