
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Статическая модель линейной многоотраслевой экономикиСодержание книги
Поиск на нашем сайте
Модель Леонтьева характеризует связи между выпуском продукции в одной отрасли и затратами, расходованием продукции всех участвующих отраслей, необходимым для обеспечения этого выпуска. Обозначим:
Так как валовый объём продукции любой i– й отрасли равен суммарному объёму продукции, потребляемой п отраслями и конечного продукта, то получаем уравнение:
В стоимостном межотраслевом балансе все величины, входящие в это уравнение, имеют стоимостное выражение. Межотраслевой баланс может быть составлен в денежной и натуральной форме. Технология производства остается на одном и том же уровне довольно длительное время, и, следовательно, объём потребления j– й отраслью продукции i– й отрасли при производстве своей продукции в объеме
это коэффициенты прямых затрат. Показывают затраты продукции i– й отрасли на производство единицы продукций j– й отрасли. Этот важный факт был установлен В. Леонтьевым на основании анализа экономики США в период перед Второй мировой войной: в течение длительного времени величины Согласно этой гипотезе выразим:
Тогда уравнения межотраслевого баланса можно переписать в виде системы уравнений:
Введем в рассмотрение соответственно:
Тогда система уравнений в матричной форме примет вид:
Это соотношение называют уравнением линейного межотраслевого баланса или модели Леонтьева. Уравнение межотраслевого баланса можно использовать в двух целях, а именно: - с одной стороны, определение объемов конечного спроса - с другой стороны, решение обратной задачи, то есть определение валового выпуска отраслей
Рассмотрим решение задачи первого типа. Известен вектор объемов валового выпуска Пример 10. Пусть вектор
Требуется вычислить вектор объемов конечного потребления Решение. Из матричного уравнения межотраслевого баланса
Находим матрицы:
Тогда по формуле получим:
Ответ: второй отрасли – 40 ед.; третьей отрасли – 60 ед.
Рассмотрим решение задачи второго типа. Для некоторого периода времени известен вектор конечного потребления Решение этой задачи в общем виде: 1. 2.
Однако такая система в силу прикладного характера данной задачи имеет особенности: все элементы матрицы A, и векторов Матрица A, все элементы которой неотрицательны, называется продуктивной, если для любого вектора Матрица Существует несколько критериев продуктивности матрицы A. Используем два из них. Первый критерий продуктивности. Матрица A продуктивна тогда и только тогда, когда матрица Второй критерий продуктивности. Матрица A с неотрицательными элементами продуктивна, если сумма элементов по любому ее столбцу (строке) не превосходит единицы:
причем хотя бы для одного столбца (строки) эта сумма строго меньше единицы. Пример 11. Таблица 11 содержит данные баланса трех отраслей промышленности за некоторый период. Таблица 11
Требуется найти объем валового выпуска продукции, если конечное потребление по отраслям увеличить соответственно до 60, 70 и 30. Решение. Выпишем векторы валового выпуска
Согласно формулам для коэффициентов прямых затрат
В результате получаем матрицу коэффициентов прямых затрат:
Требования к неотрицательности элементов всех матриц выполнены: Проверим, что матрица A удовлетворяет второму критерию продуктивности, т.е. найдем суммы ее элементов по всем строчкам и столбцам соответственно. 0,05 + 0,35 + 0,4 = 0,8 < 1; 0,1 + 0,1 + 0,4 = 0,6 < 1; 0,2 + 0,1 + 0,2 = 0,5 < 1; 0,05 + 0,15 + 0,2 = 0,4 < 1; 0,35 + 0,1 + 0,1 = 0,55 < 1; 0,4 + 0,4 + 0,2 = 1. Поскольку сумма элементов по любому ее столбцу (строке) не превосходит единицы и хотя бы для одного столбца (строки) эта сумма строго меньше единицы, то второй критерий выполнен. Для проверки первого критерия продуктивности найдем матрицу 1. По условию:
2. Найдем определитель этой матрицы, разложив по первой строке:
3. Вычисляем алгебраические дополнения.
В результате вычислений, по формуле обратной матрицы, составим матрицу полных затрат (для вычислений обратной матрицы можно использовать функции программы EXCEL, см. приложение 2):
Поскольку существует обратная матрица Вывод. Все условия продуктивности выполнены. Следовательно, существует и единственное решение уравнения Компоненты
Новый вектор конечного продукта должен иметь вид:
Новое значение валового выпуска находим по формуле
Ответ: чтобы обеспечить заданное увеличение компонент вектора конечного продукта с добычу и переработку углеводородов со 100 до 152,14, то есть на 52,14%, уровень энергетики со 100 до 135,8, то есть на 35,8%, выпуск машиностроения с 50 до 92,51, то есть на 42,51%. СПИСОК ЛИТЕРАТУРЫ
1. Анисова М.А. Практикум для студентов: В 3 ч. / Ч.2. Экономико-математические методы / Анисова М.А., Березина А.С., Жеребцова Н.А., Подкур П.Н. – Кемерово: Кемеровский институт (филиал) РГТЭУ, 2010. – 76 с. 2. Анисова М.А. Практикум для студентов: В 3 ч. / Ч.3. Экономико-математические модели / Анисова М.А., Шуревич Г.И. – Кемерово: Кемеровский институт (филиал) РГТЭУ, 2009. – 72 с. 3. Бережная Е.В. Математические методы моделирования экономических процессов: учебное пособие для вузов / Е.В. Бережная, В.И. Бережной. – М.: Финансы и статистика, 2002. – 368 с. 4. Кремер Н.Ш. Исследование операций в экономике: Учеб. пособие для вузов /Н.Ш.Кремер, Б.А. Путко, И.М. Тришин, М.Н. Фридман. – М.: ЮНИТИ – ДАНА, 2010. – 407 с. 5. Мендель А.В. Модели принятия решений: учеб.пособие для студентов вузов, обучающихся по направлениям «Экономика» и «Менеджмент»/ А.В. Мендель. – М.:ЮНИТИ-ДАНА, 2010 – 463 с. 6. Фомин Г.П. Математические методы и модели в коммерческой деятельности: учеб. / Г.П. Фомин – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2005. – 616 с. 7. Шуревич Г.И. Математика. Экономико-математические методы и модели: учеб. пособие для вузов в двух частях. Часть 2. / Г.И. Шуревич. – Кемерово: Кемеровский институт (филиал) РГТЭУ. –2006. – 348 с. 8. Шуревич Г.И. Математика. Экономико-математические методы и модели: учеб. пособие для вузов в двух частях. Часть 1 / Г.И. Шуревич. – Кемерово: Кемеровский институт (филиал) РГТЭУ. –2003. – 308 с. Приложение 1
Производные основных элементарных функций
Приложение 2 Функция МОБР Синтаксис: МОБР(Массив) Результат: Возвращает обратную матрицу для матрицы, хранящейся в массиве. Аргумент: Массив - числовой массив интервала данных с равным количеством строк и столбцов.
Пример использования. Введите данные исходной матрицы А1:С3. Выберите ячейки для отображения обратной матрицы, например A5:С7. Выберите команду «Вставить функцию», появится диалоговое окно (см. рис. 4).
Рис. 4. Окно диалога для функции МОБР
В разделе «Категория» выберите значение «Математические», в разделе «Выберите функцию» - МОБР. В качестве аргумента укажите массив А1:С3 и нажмите сочетание клавиш CTRL+SHIFT+ВВОД. В массиве A5:С7 будут указаны значения коэффициентов обратной матрицы.
СОДЕРЖАНИЕ Предисловие. 3 1. Правила и порядок выполнения контрольной работы.. 4 2. Тематический план дисциплины.. 5 3. Содержание дисциплины.. 5 4. Контрольные вопросы.. 7 5. Варианты контрольной работы.. 9 6. Указания по выполнению контрольной работы.. 19 6.1. Модель поведения потребителя. 19 6.2. Модели поведения производителей. 26 6.3. Поведение фирм на конкурентных рынках. 32 6.4. Статическая модель линейной многоотраслевой экономики. 35 Список литературы.. 44 Приложение. 45
Учебное издание
МАТЕМАТИЧЕСКАЯ ЭКОНОМИКА Методические указания по выполнению контрольной работы для студентов направления подготовки 230700 «Прикладная информатика» заочной формы обучения
Составитель Анисова Мария Александровна
Подписано в печать 11.03.2014. Формат 60х84 1/16. Гарнитура «Таймс». Усл. печ. л. 3. Тираж 40 экз. Заказ № 178 ________________________________________________ Кемеровский институт (филиал) РГТЭУ. 650992, г. Кемерово, пр. Кузнецкий, 39
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 358; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.007 с.) |

 – общий валовый объём продукции i –й отрасли,
– общий валовый объём продукции i –й отрасли, 
 – объём продукции i –йотрасли, потребляемый j –й отраслью в процессе производства при выпуске объёма продукции
– объём продукции i –йотрасли, потребляемый j –й отраслью в процессе производства при выпуске объёма продукции 
 – объём конечного продукта i– й отрасли для непроизводственного потребления,
– объём конечного продукта i– й отрасли для непроизводственного потребления,  .
. ,
,  .
. единиц есть технологическая константа:
единиц есть технологическая константа: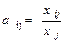 ,
, 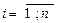 ,
, 
 - коэффициенты прямых затрат меняются очень незначительно и потому могут рассматриваться как постоянные числа.
- коэффициенты прямых затрат меняются очень незначительно и потому могут рассматриваться как постоянные числа. .
.
 – вектор-столбец объемов производственной продукции (вектор валового выпуска);
– вектор-столбец объемов производственной продукции (вектор валового выпуска); – вектор-столбец объемов продукции конечного потребления (вектор конечного потребления);
– вектор-столбец объемов продукции конечного потребления (вектор конечного потребления); – матрица коэффициентов прямых затрат (технологическая или структурная матрица).
– матрица коэффициентов прямых затрат (технологическая или структурная матрица).
 на каждый i -й продукт по известному валовому выпуску
на каждый i -й продукт по известному валовому выпуску  ,
, 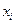 по заданному конечному спросу
по заданному конечному спросу 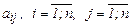 .
. . Требуется вычислить вектор объемов конечного потребления
. Требуется вычислить вектор объемов конечного потребления 
 ,
, 
 .
.
 .
.

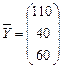 , то есть объемы конечного продукта составляют для: первой отрасли – 110 ед.;
, то есть объемы конечного продукта составляют для: первой отрасли – 110 ед.; и матрица коэффициентов прямых затрат A. Требуется определить вектор валового выпуска
и матрица коэффициентов прямых затрат A. Требуется определить вектор валового выпуска 



 с неотрицательными компонентами существует решение уравнения вектор
с неотрицательными компонентами существует решение уравнения вектор  , все элементы которого неотрицательны. В таком случае и модель Леонтьева называется продуктивной.
, все элементы которого неотрицательны. В таком случае и модель Леонтьева называется продуктивной. называется матрицей полных затрат.
называется матрицей полных затрат. существует и ее элементы неотрицательны.
существует и ее элементы неотрицательны. ,
,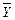 :
: ,
,  ,
, , вычислим
, вычислим  :
: ;
; ;
;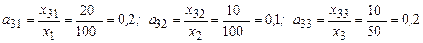 .
. .
. неотрицателен;
неотрицателен;  неотрицателен; A – из неотрицательных элементов.
неотрицателен; A – из неотрицательных элементов. ;
;  ;
; .
.

 ,
, ,
,
 ,
, ,
, ,
,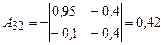 ,
, .
. .
.
 неизвестного
неизвестного 
 .
. .
.
 до
до 
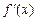
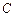


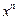


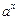






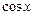



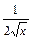




 , где
, где  :
: 




