
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Модель поведения потребителяСодержание книги Поиск на нашем сайте Теория потребления — одна из основополагающих дисциплин микроэкономики. Она исследует экономические решения, в особенности в области потребления частными экономическими агентами. Теория потребления основывается на допущении, что агент стремится к удовлетворению всех своих материальных и нематериальных потребностей. Удовлетворение потребностей является главным смыслом экономической деятельности. Чем лучше оно удается агенту, тем выше польза как экономическое понятие. Благо в теории потребления — любой объект потребления, доставляющий определенное удовлетворение потребителю. Блага потребляются, как правило, в определенных наборах. Набор благ - совокупность конкретных видов благ в определенных объемах, потребляемых в данный период. Необходимыми предпосылками теории потребительского выбора являются следующие аксиомы. Аксиома полной упорядоченности предпочтений потребителя. Эта аксиома предполагает, что потребитель сам должен принимать решения относительно потребления и осуществлять их. Аксиома транзитивности предпочтений потребителя. Чтобы принять определенное решение и реализовать его, потребитель должен последовательно переносить предпочтения с одних благ и их наборов на другие. Предположение о транзитивности гарантирует рациональность (согласованность) предпочтений. В ином случае поведение потребителя противоречиво. В этой связи говорят, что «предпочтения свернулись в кольцо», т. е. изменились вкусы. Аксиома о ненасыщаемости потребностей гласит, что потребители всегда предпочитают большее количество любого блага меньшему (или «больше всегда лучше»). Эти три предпосылки необходимы для того, чтобы определить функцию полезности. Функция полезности — это целевая функция действий потребителя в потребительском выборе, выражающая процесс упорядочивания выбираемых потребителем наборов благ до уровня удовлетворения потребностей. Полезность выражает меру удовлетворения, которое получает субъект от потребления благ. Полезность понятие сугубо индивидуальное: полезное для одного субъекта может быть бесполезно для другого. Полезность зависит от потребительских свойств благ и от самого процесса потребления, от того, кто и как удовлетворяет свои потребности. Полезность имеет свойство порядковой измеримости, когда альтернативы могут быть ранжированы, но не имеет свойства количественной измеримости. Обозначим функцию полезности:
где индекс
Тогда предельная полезность — это приращение степени удовлетворения (полезности) при потреблении или использовании дополнительной единицы блага за определенный период времени. Предельной полезностью называют полезность, равную приращению общей полезности вследствие покупки дополнительной единицы данного блага:
Свойства функции полезности: 1. 2. 3. Поверхность безразличия описывается уравнением Предельная норма замещения товаров выражается через отношение их предельных полезностей, взятое со знаком минус:
Модель поведения потребителя Покупатель при выборе приобретаемых благ обладает определенными индивидуальными предпочтениями, но он ограничен в удовлетворении своих предпочтений бюджетным ограничением. Бюджетное ограничение — это фактор, ограничивающий покупательные возможности субъекта в виде цен на блага или уровня дохода. Составим математическую модель задачи поведения потребителя для двух благ в виде: 1. Переменные постоянные величины
2. Целевая функция: 3. Система ограничений (бюджетное ограничение):
Получили задачу на условный экстремум. Решение этой задачи может быть выполнено несколькими способами. 1) Геометрический метод решения. Заключается в нахождении координат точки касания кривой безразличия с бюджетным ограничением. 2) Аналитическое решение для задачи с двумя переменными – приведение целевой функции к одной переменной (значения производных основных функций можно посмотреть в приложении 1). 3) Аналитическое решение (может быть использовано и для задачи с любым количеством переменных) - введение функции Лагранжа:
Рассмотрим применение всех способов далее на примерах. Пример 1. Проверить, может ли функция: Решение. Если x 1>1; x 2>1, то 1. 2. 3. Ответ: условия функции полезности выполнены, Пример 2. Построить карту безразличия для функции полезности: Решение. 1.
Рис. 1. Карта безразличия функции
Графически это гиперболы в первом квадранте, например а) при C = 1 получаем б) при С = 2 получаем Пример 3. Найти геометрическое решение задачи максимизации индивидуальной функции полезности Решение. 1. Из
Запишем ее уравнение в отрезках 2. Построим на системе координат (см. на рис. 2) бюджетную прямую – прямую АВ и кривую безразличия
Рис. 2. Геометрическое решение
3. Решим систему уравнений графически.
1) 2) 3) Ответ: оптимальный набор благ x 1 » 2; x 2 » 1. Пример 4. Найти аналитическое решение задачи максимизации индивидуальной функции полезности Решение. Известны: Требуется найти значения Приведенем функцию полезности к зависимости от одной переменной. 1. Из 2. Подставим найденное значение x2 в целевую функцию
3. Исследуем
Для проверки вида экстремума можно использовать вторую производную: 4. Находим Ответ: оптимальный набор благ Пример 5. Найти решение задачи максимизации функции полезности Решение. Известны: Требуется найти значения 1. Составим функцию Лагранжа:
2. Найдем первые частные производные функции
3. Разделим поэлементно первое уравнение на второе, получим:
4. Используя третье равенство в последней системе уравнений, получим:
5. Ответ: оптимальный набор благ
|
||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 472; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.01 с.) |

 ,
,  ,
, 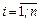 ,
, - вид блага
- вид блага 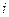 ,
,  - количество
- количество 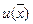 числовое значение функции полезности.
числовое значение функции полезности. ,
,  ,
,  ,
, 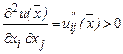 ,
,  ,
,  .
. , где C – любая константа. При n = 2 имеем
, где C – любая константа. При n = 2 имеем  , откуда
, откуда  .
.
 .
.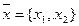 ,
,  - вектор благ;
- вектор благ; - цены на блага;
- цены на блага; - доход потребителя.
- доход потребителя. ;
;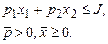
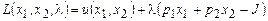 .
. , при x 1>1; x 2>1 являться функцией полезности.
, при x 1>1; x 2>1 являться функцией полезности. .
.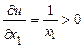 ;
;  .
. .
. .
.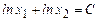 , (C = const);
, (C = const);  или
или 

 ;
; (см. рис. 1).
(см. рис. 1).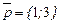 ,
, 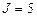 .
. при p 1 = 1, p 2 = 3 и J = 5 получаем:
при p 1 = 1, p 2 = 3 и J = 5 получаем: – это бюджетная прямая.
– это бюджетная прямая.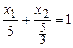 .
. , то есть
, то есть 
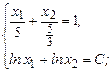 откуда
откуда 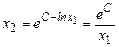 – гипербола.
– гипербола. при С = 1;
при С = 1; при
при  ;
; при
при 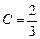 .
. и J =5.
и J =5.
 .
. .
. . Получим функцию одного аргумента x1:
. Получим функцию одного аргумента x1: .
. на экстремум с помощью производной по стандартной схеме:
на экстремум с помощью производной по стандартной схеме: ;
; если
если  ;
; ;
; .
. , следовательно, это точка максимума.
, следовательно, это точка максимума. .
.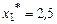 ,
, 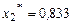 .
.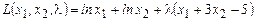 .
. по переменным
по переменным  и приравняем их к нулю:
и приравняем их к нулю:
 , откуда следует
, откуда следует или
или .
. ;
;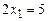 ;
;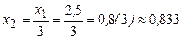 .
.


