
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дослідження швидкості вихідної ланки механізмуСодержание книги
Поиск на нашем сайте
Дослідження руху вихідної ланки механізму (повзун 5) зводиться до визначення положення і швидкості повзуна 5 за цикл усталеного руху механізму. Розглянемо аналітичний метод. Складемо розрахункову схему векторних замкнутих контурів (рис.1.3). Число таких контурів визначається за формулою
де р – загальне число кінематичних пар у механізмі. На рис.1.3 показані два замкнутих векторних контури ОАО1О і О1СВКО1. Розглянемо перший із них ОАО1О. Запишемо умову замкнутості контуру
Проекціюємо замкнутий векторний контур ОАО1О на осі координат. Отримаємо систему рівнянь
Із системи (1.1) визначаємо кут
Розглянемо другий замкнутий векторний контур О1СВКО1. Умова замкнутості контуру
Із записаного векторного рівняння отримуємо таку систему рівнянь
Із другого рівняння системи (1.3) визначаємо кут
Знаючи кут
Швидкість точки В можна визначити із системи лінійних рівнянь, які записуються шляхом диференціювання системи рівнянь (1.1) і (1.3) по часу t
Ордината точки В
Програма ( варіант1-й ) Вхідні дані
Програма ( варіант2-й ) Вхідні дані

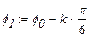
Перше наближене значення невідомих параметрів системи нелінійних рівнянь
Розв’язок системи нелінійних рівнянь у к -тому положенні
Перше наближене значення невідомих параметрів системи лінійних рівнянь
Розв’язок системи лінійних рівнянь у к -тому положенні механізму
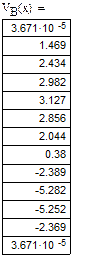
Результати розв’язку системи нелінійних рівнянь і системи лінійних рівнянь заносимо у таблицю. Міняємо значення параметра к, яке відповідає наступному номеру положення кривошипа і новий результат обчислень знову заносимо у таблицю. Так повторити 12 раз. Результати, які отримані за допомогою програми Mathcad, заносимо у табл.1.2.
Таблиця 1.2 – Результати досліджень руху вихідної ланки
Користуючись числовими значеннями, поданими у табл.1.1, будуємо графік швидкості повзуна 5 в залежності від кута повороту кривошипа
По осі абсцис відкладаємо 12 положень кривошипа. Довжину осі абсцис (відрізок 0-12) беремо рівною 120 мм.
Визначення зведеного моменту сил опору Визначаємо числові значення зведеного моменту сил опору за формулою
Оскільки, сили ваги значно менші за величиною від сили опору F то першими нехтуємо. Тоді
Результати обчислень заносимо у табл.1.3. Таблиця 1.3 –Результати енергетичного розрахунку механізму
Для побудови графіка
Значення ординат заносимо у табл.1.2. Через точки 0,1,2...12 осі абсцис проводимо вертикальні лінії і відкладаємо на них знайдені значення ординат. Кінці проведених ординат з’єднуємо плавною кривою і отримаємо графік функції Визначення роботи сил опору
Роботу сил опору визначаємо методом числового інтегрування функції
де
Визначаємо роботу
Аналогічно обчислюємо
Обчислюємо ординати графіка За результатами обчислень будуємо графік роботи сил корисного опору. Через точки 0,1,2...12 осі абсцис проводимо вертикальні лінії і відкладаємо на них знайдені ординати. Одержані точки з’єднуємо плавною кривою і отримаємо графік функції
Визначення моменту рушійних сил і потужності,
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 286; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.006 с.) |

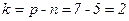 ,
,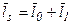 .
.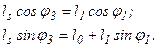 (1.1)
(1.1)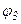
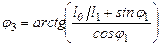 . (1.2)
. (1.2)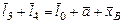 .
.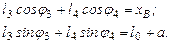 (1.3)
(1.3)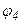
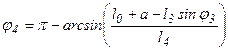 . (1.4)
. (1.4)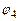 обчислюємо абсцису точки В і її швидкість
обчислюємо абсцису точки В і її швидкість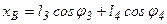 . (1.5)
. (1.5)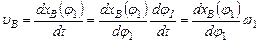 . (1.6)
. (1.6)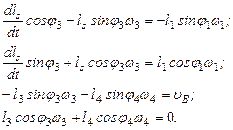 (1.7)
(1.7)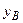 постійна. За складеним алгоритмом (формули (1.2), (1.4), (1.5), (1.6), (1.7)) визначаємо положення і швидкість точки В у 12-ти положеннях механізму. Для цього використовуємо програму Mathcad. Програми і результати обчислень наведені нижче.
постійна. За складеним алгоритмом (формули (1.2), (1.4), (1.5), (1.6), (1.7)) визначаємо положення і швидкість точки В у 12-ти положеннях механізму. Для цього використовуємо програму Mathcad. Програми і результати обчислень наведені нижче.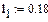
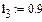
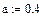
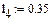
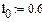
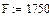
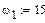

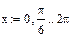

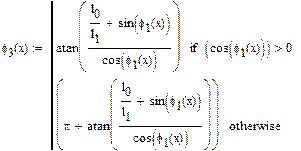
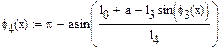

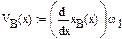 Результати обчислень
Результати обчислень

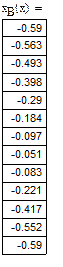
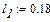


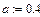
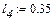
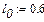
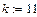
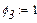
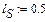
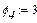
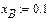
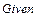
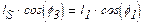

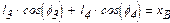
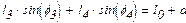

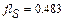
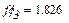
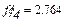
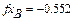
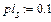
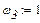
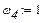
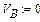

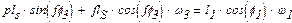
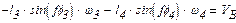
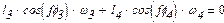
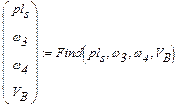
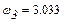
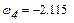
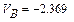
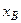
 (рис.1.4). По осі ординат відкладаємо швидкість
(рис.1.4). По осі ординат відкладаємо швидкість 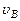 використовуючи масштабний коефіцієнт
використовуючи масштабний коефіцієнт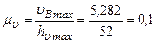 м/с∙мм.
м/с∙мм. .
.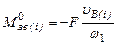 .
.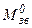 ,
(Н·м)
,
(Н·м)
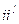 ,
мм
,
мм
 ,
Дж
,
Дж
 ,
мм
,
мм
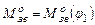 задаємось масшабним коефіцієнтом
задаємось масшабним коефіцієнтом 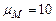 Нм/мм. Обчислюємо ординати графіка
Нм/мм. Обчислюємо ординати графіка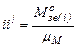 .
.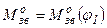 (рис.1.4).
(рис.1.4).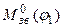 , яка задана масивом чисел (табл.1.2), за формулою
, яка задана масивом чисел (табл.1.2), за формулою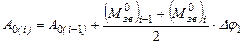 ,
,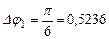 рад.
рад.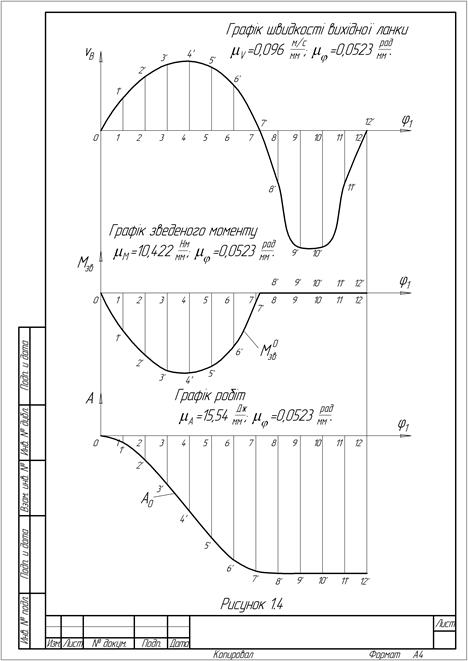
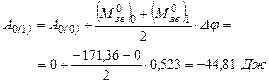
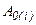 для інших положень механізму і результати заносимо у таблицю 1.2. Будуємо графік роботи сил корисного опору. Приймаємо масштабний коефіцієнт осі ординат:
для інших положень механізму і результати заносимо у таблицю 1.2. Будуємо графік роботи сил корисного опору. Приймаємо масштабний коефіцієнт осі ординат: .
. і результати заносимо у табл.1.2.
і результати заносимо у табл.1.2.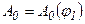 (рис.1.4).
(рис.1.4).


