Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Розрахунково-графічної роботиСодержание книги Поиск на нашем сайте
Структурний аналіз механізму. Структурний аналіз є базою кінематичного та силового аналізу механізмів. В результаті структурного аналізу визначається число ступенів вільності ланок механізму, кількість і клас структурних груп, що входять до його складу, порядок їх приєднання, клас механізму в цілому. Для прикладу розглянемо структурний аналіз механізму поперечно-стругального верстата (рис.5.1). У цьому механізмі n=5, р5 = 7, тоді число степенів вільності:
Отже, в цьому механізмі повинна бути одна вхідна ланка (наприклад, кривошип ОА). Найчастіше першу структурну групу у порядку від’єднання від механізму утворюють ланки, які найбільш віддалені від вхідної ланки групи. У даному випадку таку групу утворюють ланки 4 і 5 і кінематичні пари С (3,4), D (4,5), D с(5,0). Ця структурна група належить до 2-го класу (класифікація І.І. Артоболевського). У дужках вказані номери ланок, які утворюють одну пару. Частина механізму, яка залишилась, має також ступінь вільності W=1 (n =3, р 5=4), і з неї можна знову виділити групу 2-го класу, яка складається із ланок 2 і 3 і трьох кінематичних пар А (1,2), А 3(2, 3), В(3,0). І, нарешті, після від’єднання структурних груп залишається один механізм І-го класу, який складається із стояка 0 і кривошипа 1.
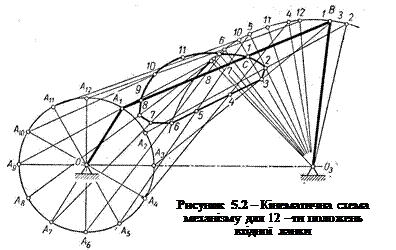
де 1 – механізм 1-го класу; ІІ – структурна група 2-го класу. Номери ланок, що утворюють механізм 1-го класу (ланка 1) або структурні групи (ланки 2, 3 і 4, 5), вказані у дужках. Побудова положень ланок механізму. Побудову положень ланок (планів) механізму 2-го класу можна здійснювати методом засічок. Розглянемо це питання на прикладі кривошипно-коромислового механізму, кінематична схема та закон руху кривошипа ОА (w1 = сonst) якого задані на рис.5.2. Побудову здійснюють у певному масштабі. Для цього використовують масштабний коефіцієнт, який у загальному вигляді є відношенням фізичної величини (шляху, швидкості тощо) до довжини відрізка, який цю величину зображує на рисунку. Масштабний коефіцієнт, який у подальшому будемо називати масштабом, позначаємо літерою mi з індексом тієї величини, яку зображено графічно. Масштаб mi має розмірність, у чисельнику якої – розмірність величини, яка зображується, у знаменнику – розмірність довжини відрізка (мм). Наприклад, коли зображувати лінійні розміри механізму, масштаб (м/мм) визначатиметься за формулою
де lОА - дійсна довжина кривошипа ОА, м; ОА – довжина відрізка ОА, мм, який зображує його на рис.5.2. Щоб знайти методом дугових засічок положення всіх точок і ланок механізму, необхідно послідовно розглянути рух кожної ланки, від вхідної до вихідної, у такому порядку, у якому вони приєднуються до механізму. Кривошип ОА здійснює рівномірний обертальний рух (w 1 = сonst) навколо нерухомого центра О. Шатун АВ здійснює складний рух: центр шарніра А рухається по колу радіуса ОА, центр шарніра В – по колу з постійним радіусом О 3 В, який шарнірно зв’язаний із шатуном АВ.
За початкове положення механізму, як правило, вибирають одне з його крайніх положень. Не буде помилкою, якщо взяти будь-яке. Нехай таким положенням буде випадок, коли кривошип займає верхнє вертикальне положення. Далі поділимо траєкторію точки А на довільне вибране число рівних частин, наприклад 12, як це показано на рис.5.2. Точки поділу позначимо А0, А1, А2,…, А12 у напрямі обертання кривошипа. Тобто перехід з одного положення в інше здійснюється за час Т /12, де Т – період обертання кривошипа (Т= 60 /n,с; n – частота обертання кривошипа, об/ хв).
Положення точки В знайдемо методом дугових засічок, враховуючи, що довжина шатуна АВ протягом руху залишається незмінною. Для цього з одержаних точок А0, А1, А2,…, А12 радіусом АВ зробимо дугові засічки на траєкторії точки В, у результаті чого знайдемо положення центрів шарніра В-В0, В1, В2,…, В12. З’єднання точки Аі і Ві відрізками Аі Ві, одержимо положення шатуна АВ і повзуна В (і =0, 1, 2…, 12). Таким самим способом побудуємо траєкторію точки С, яка лежить на шатуні АВ (див. рис.5.1). Для цього з точки А і зробимо на відповідних положеннях АіВі дугові засічки радіусом АС, які визначають точки Сі. Послідовно з’єднавши точки Сі плавною кривою, одержимо траєкторію точки С. Через те, що точка С лежить на шатуні, її траєкторію називають шатунною кривою. Якщо до складу механізму входять декілька груп, то побудова їхніх планів здійснюється аналогічно. Побудова планів швидкостей і прискорень. У даному підрозділі ми не будемо розглядати метод побудови планів швидкостей і прискорень оскільки вважаємо, що цей метод дуже досконало розглянутий у всіх підручниках з теорії механізмів і машин.
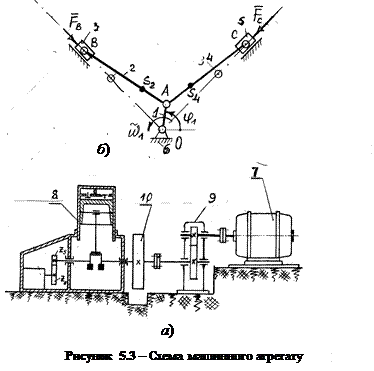
Визначення потужності, необхідної для роботи механізму. Розглянемо машинний агрегат, кінематична схема якого зображена на рис.5.3. Машинний агрегат складається із електродвигуна 7, компресора 8 і передаточного механізму (редуктор) 9. За ланку зведення виберемо колінчастий вал компресора ОА. Кутова швидкість ланки ОА 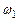 є постійна. Коливання швидкості є постійна. Коливання швидкості 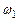 під час усталеного періоду роботи механізму не значні, тому ними нехтуємо. під час усталеного періоду роботи механізму не значні, тому ними нехтуємо.
Тоді потужність виконавчого механізму визначимо за формулою
де Таким чином визначення потужності виконавчого механізму зводиться до визначення Розглянемо послідовність визначення зведеного моменту рушійних сил 1) Визначаємо зведений момент сил опору Зведений момент сил опору (силами ваги нехтуємо) знаходиться для 12-ти положень механізму за формулою:
Знак мінус ставиться у тому випадку, коли вектор сили і вектор швидкості точки її прикладання мають протилежні напрямки, плюс – коли співпадають за напрямком. За результатами обчислень будуємо графік 2) Будуємо графік роботи сил опору Для цього розглянемо два положення механізму з номерами і-1 та і, яким відповідає обертання кривошипа на кут
а за період від початку циклу
За результатами обчислень (формули (5.3) і (5.4)) викреслюється графік Робота рушійних сил за цикл усталеного руху є рівною роботі сил опору за цикл АР=АО. Вважаємо зведений момент рушійних сил Тоді графік роботи рушійних сил Роботу рушійних сил АР можна визначити за формулою
Якщо період усталеного руху дорівнює
Із залежності (5.5) визначаємо зведений момент рушійних сил
Тепер, за формулою (5.1), визначаємо потужність рушійних сил, яка необхідна для виконання технологічного процесу виконавчим механізмом.
|
|||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 223; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.16.40 (0.009 с.) |


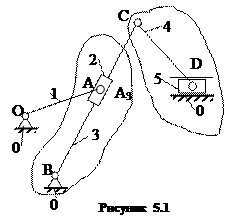 Отже, механізм, зображений на рис.5.1, є механізмом 2-го класу. Склад і послідовність приєднання структурних груп механізму можна виразити формулою будови механізму. Наприклад, формула будови механізму, який зображено на рис.4.1, має вигляд:
Отже, механізм, зображений на рис.5.1, є механізмом 2-го класу. Склад і послідовність приєднання структурних груп механізму можна виразити формулою будови механізму. Наприклад, формула будови механізму, який зображено на рис.4.1, має вигляд: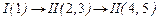 ,
, ,
,
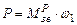 , (5.1)
, (5.1)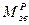 - зведений до ланки ОА момент рушійних сил.
- зведений до ланки ОА момент рушійних сил.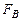 ,
, 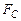 .
.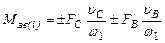 . (5.2)
. (5.2)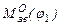 (рис.5.4, а)
(рис.5.4, а)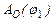 методом числового інтегрування.
методом числового інтегрування.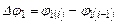 . Зведені моменти сил опору в цих положеннях відповідно мають значення
. Зведені моменти сил опору в цих положеннях відповідно мають значення 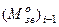 і
і 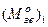 . Робота сил опору на цьому відрізку приблизно дорівнює
. Робота сил опору на цьому відрізку приблизно дорівнює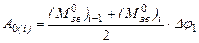 , (5.3)
, (5.3)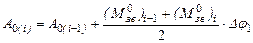 (5.4)
(5.4)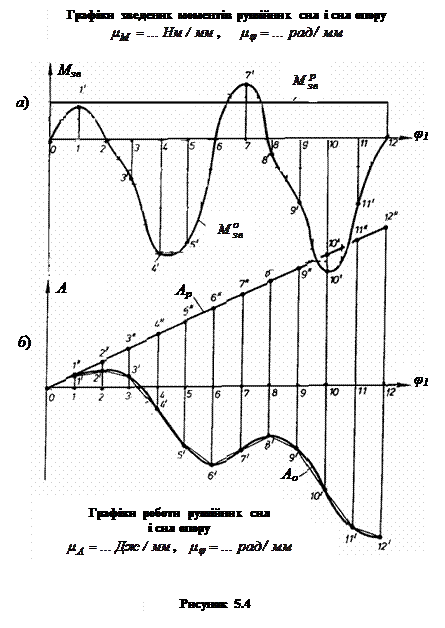
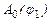 (рис.5.4, б).
(рис.5.4, б).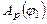 є лінійною функцією (рис.5.2, б). Щоб його побудувати необхідно відкласти ординату
є лінійною функцією (рис.5.2, б). Щоб його побудувати необхідно відкласти ординату  величиною рівною ординаті
величиною рівною ординаті 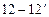 і точку
і точку 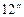 з’єднати прямою з початком системи координат.
з’єднати прямою з початком системи координат.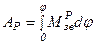 .
.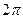 , тоді
, тоді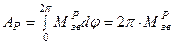 . (5.5)
. (5.5)