
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
М. 12. 18. Каким образом рассчитывается устойчивость сооружения на опрокидывание.Содержание книги
Поиск на нашем сайте
Устойчивость на опрокидывание (рис.М.12.18,а) оценивается по отношению моментов сил удерживающих и сил опрокидывающих, взятых относительно крайней точки. При этом считается, что сооружение как бы чуть приподнялось и поэтому реакция основания в виде сосредоточенной силы приложена в крайней точке, а, следовательно, в условие равновесия моментов она не войдет, так как проходит через этот полюс. Для того, чтобы увеличить устойчивость на опрокидывание, следует ввести слева у сооружения консоль (рис.М.12.18,б). В случае деформируемости основания вращение при опрокидывании происходит не вокруг одной крайней точки, а сооружение "входит" в грунт основания, поэтому и вращение произойдет вокруг центра, располагающегося в пределах подошвы сооружения (рис.М.12.18,в). Опрокидыванию предшествует крен сооружения. Обычно стремятся не допускать отрыва подошвы от грунта, кроме особых случаев (например, действия сейсмических сил), и ограничивать соотношение между максимальным и минимальным вертикальными напряжениями (рис.12.18,г). При установлении величин этих максимальных напряжений следует учитывать также и касательные усилия, возникающие по подошве сооружения.
М.13. ТЕОРИЯ ПРЕДЕЛЬНОГО РАВНОВЕСИЯ ГРУНТОВ М.13.1. Каким образом записывается условие предельного равновесия в главных напряжениях? Каким образом это условие преобразуется в зависимость, в которую входят все три компонента напряжений (в декартовых координатах)? Условие предельного равновесия в главных напряжениях имеет вид
С помощью круга Мора и теоремы Пифагора, согласно которой
а также учитывая, что
М.13.2*. Сколько неизвестных компонентов напряжений мы имеем в случае плоской задачи, осесимметричной задачи, пространственной задачи в общем случае? В случае плоской задачи мы имеем три неизвестных компонента напряжений, в случае осесимметричной задачи четыре, а для пространственной задачи в общем случае шесть компонентов напряжений. М.13.3*. Какие дополнительные зависимости привлекаются к уравнениям равновесия в теории предельного равновесия сыпучей среды в плоской, осесимметричной и пространственной задачах и сколько этих дополнительных зависимостей? К двум уравнениям равновесия в случае плоской задачи привлекается одно условие, связывающее компоненты напряжений, - условие предельного равновесия. В случае осесимметричной задачи к двум уравнениям равновесия (проекции на оси координат) привлекается также одно условие предельного равновесия, а дополнительным, поскольку компонентов в уравнениях четыре, является условие равенства между собой двух главных напряжений (промежуточное равно минимальному или максимальному). В случае пространственной задачи мы имеем три уравнения равновесия и одно уравнение предельного равновесия - таким образом, не хватает двух уравнений. М.13.4*. В каких случаях общая система уравнений теории предельного равновесия является замкнутой? В каких случаях и сколько уравнений не хватает для получения замкнутости системы? Что называется условием "полной" и "неполной" сыпучести? В случае плоской задачи система оказывается полностью замкнутой. В случае осесимметричной задачи не хватает одного уравнения и привлекается условие "полной сыпучести" путем приравнивания промежуточного главного напряжения минимальному или максимальному, после чего система становится замкнутой. Если не привлечь этого условия, то система будет незамкнутой (неполной). В случае пространственной задачи не хватает двух уравнений и система оказывается незамкнутой. М.13.5*. Чему равен порядок системы дифференциальных уравнений в частных производных? Какой порядок имеет система дифференциальных уравнений теории упругости (плоская задача) и теории предельного равновесия сыпучей среды? Порядок системы дифференциальных уравнений в частных производных равен сумме порядков входящих в нее уравнений. Система дифференциальных уравнений теории упругости имеет четвертый порядок, а система уравнений теории предельного равновесия - второй порядок, так как уравнение предельного равновесия включает только компоненты напряжений, но не их производные. Это уравнение второй степени, но нулевого порядка. М.13.6. Что дают нам произвольные постоянные интегрирования и произвольные функции интегрирования, получаемые в результате решения основной системы уравнений теории упругости и теории предельного равновесия сыпучей среды? Произвольные постоянные интегрирования позволяют из общего решения системы обыкновенных дифференциальных уравнений получить частное решение, удовлетворяющее краевым условиям. Произвольные функции, получающиеся в результате интегрирования системы дифференциальных уравнений в частных производных, позволяют получить частное решение, удовлетворяющее граничным условиям рассматриваемой задачи. В теории упругости и в теории предельного равновесия это - напряжения на границе области. Вдоль участка границы возможно задать два граничных условия - в теории предельного равновесия это нормальное и тангенциальное напряжения на границе. В теории упругости граничные условия могут быть заданы в напряжениях или перемещениях, могут быть и смешанного типа. М.13.7*. Чем отличаются дифференциальные уравнения гиперболического, параболического и эллиптического типов? Что называется характеристикой дифференциального уравнения и как ее найти? Сколько существует характеристик? Характеристикой дифференциального уравнения называется линия на плоскости, вдоль которой частные производные не могут быть однозначно определены (детерминант оказывается равным нулю). Характеристики системы дифференциальных уравнений могут быть найдены путем приравнивания всех детерминантов системы нулю. Система гиперболического типа (теория предельного равновесия сыпучей среды) имеет два семейства действительных характеристик, система параболического типа (теория фильтрационной консолидации) - одно и система эллиптического типа (теория упругости) - два семейства мнимых характеристик. М.13.8*. С чем совпадают характеристики системы дифференциальных уравнений теории предельного равновесия сыпучей среды? Сколько систем характеристик мы имеем в плоской задаче теории предельного равновесия? Характеристики системы дифференциальных уравнений теории предельного равновесия сыпучей среды совпадают с линиями скольжения. В плоской задаче мы имеем два семейства характеристик, следовательно, два семейства линий скольжения, вдоль которых выполняется условие
|
||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 349; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.189.184.99 (0.006 с.) |


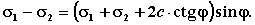

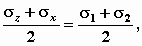 получим следующее условие:
получим следующее условие: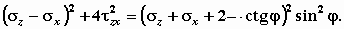
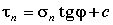 .
.


