
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вивчення гармонічних коливань на прикладі математичного маятника.Содержание книги
Поиск на нашем сайте
Прилади та приладдя: Установка з маятником і градусною шкалою, лінійка, секундомір. Мета роботи: вивчення основних законів гармонічного коливання.
Коротка теорія і метод вимірювання
Гармонічними називають коливання тіла, близьке до положення рівноваги під дією сили, пропорційної зміщенню тіла з положення рівноваги і направленої до положення рівноваги F = - cx, (1) де c - коефіцієнт пружної (квазіпружної) сили. Знак мінус вказує на протилежність x і F. Якщо сила F є єдина прикладена до тіла, то вона спричинить його прискорення а і згідно з ІІ законом Ньютона F = m a = m d2x /d t2, (2) де m - маса тіла; d2x/dt2 - повторна (друга) похідна від зміщення за часом - прискорення тіла. Із співвідношень (1) і (2) одержуємо рівняння, яке називають диференціальним рівнянням гармонічного коливання: m d2x/d t2 = - cx, (3) розв’язком якого є x = A sin (ω t + φ), (4) де: A - амплітуда - максимальне відхилення від положення рівноваги, ω t + φ -фаза коливання; φ - початкова фаза коливання, що відповідає моменту часу t = 0; ω - кругова або циклічна частота коливань, що дорівнює ω = Найбільш простою наближеною моделлю гармонічного коливання може служити рух математичного маятника (рис.1), початково відхиленого від положення рівноваги на деякий невеликий кут (α ≈ 5˚). Діюча на матеріальну точку сила тяжіння - P = mg розкладається на дві взаємно перпендикулярні складові. Складова F1 і сила натягу нитки створюють доцентрове прискорення, а друга складова F викликає дотичне прискорення точки, що рухається по колу. За подібністю відповідних трикутників визначаємо: F = P x / l, (6) де l довжина нитки. При малих кутах α можна знехтувати відхиленням траєкторії від прямої і вважати, що дотичне прискорення дорівнює d2x/dt2. Тоді виявляється справедливим (1) і, випливаючі з нього, (3) і (4). При цьому в ролі коефіцієнта пружної сили виступає відношення: c = P / l, (7)
що називається коєфіціентом квазіпружної сили, тому що сила F в (4), звичайно ж, не є пружною, хоч і схожа з нею.
Підставляючи k із (7) в (5), одержуємо: ω = Розглянемо коливання (4). Зміщення з положення рівноваги х періодичне в часі, і це відображується функцією синус, яка має період 2π. Зміні фази коливання на 2π відповідає найменший проміжок часу, через який повторюється процес коливання (період коливання). Якщо позначити період коливання T, то виявляється що T ω = 2π/Т, звідки:
T = 2π / ω (9) що у випадку математичного маятника виглядає як T = 2π Отже, при гармонічних коливаннях період коливань математичного маятника, як це випливає з (10), не залежить від амплітуди коливань та маси і визначається довжиною маятника та прискорення вільного падіння тіла. За відомими значеннями l і g з (8) та (10) можна розрахувати циклічну частоту і період коливань. З другого боку, період коливань нескладно визначити експериментально, а по ньому розрахувати за (9) циклічну частоту коливань. В роботі використовується модель математичного маятника у вигляді металевої кульки, підвищеної на довгій нитці. Вивчається не тільки гармонічні, але й ангармонічні коливання, коли кут відхилення перевершує допустимі для гармонічних коливань значення в 3-4 рази.
Порядок виконання роботи:
1. Ознайомитися з установкою виміряти довжину маятника l (від центра кульки). За формулою (8) обчислити теоретичне значення циклічної частоти ω, а за (10) - період T. 2. Відхилити маятник на α = 4-6˚ і, відпустити його, виміряти секундоміром час Δt здійснення 50 коливань. Обчислити період коливань T = t/50. За знайденим T за співвідношенням (9) обчислити ω. Визначити амплітуду коливань A з трикутника (рис.1): A = xmax = l sin αmax За знайденими величинами написати рівняння (4) при φ = π /2. 3. Повторити дії п.2 для α2 = 12-15˚ та для α3 =18-20 ˚. 4. Оцінити для кожного α відхилення одержаних з дослідів значень ω від їх теоретичного значення. Дані вимірів і обчислень занести до таблиці:
Дайте відповіді на запитання:
1. Як залежить точність виконання законів гармонічних коливань від кута відхилення математичного маятника? 2. Приймаючи відносну похибку 0,03, оцінити за даними табл.1, для яких кутів можна застосовувати закони гармонічних коливань?
Лабораторна робота № 11.
|
|||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 412; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.101.224 (0.01 с.) |

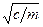 (5)
(5)

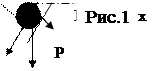
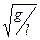 (8)
(8) (10)
(10)


