
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дослідження відношення маси тяжіння до маси інерції.Содержание книги
Поиск на нашем сайте
Прилади та приладдя: відцентрова машина з двома тягарями та градусною шкалою, тахометром і лабораторним трансформатором. Мета роботи: поглибити поняття маси як міри інертності та міри тяжіння тіл. Коротка теорія та метод дослідження
В інерціальних системах координат точно дотримується ІІ закон Ньютона в формі: a =F/ m, (1) та закон тяжіння: Fт = γ mт Mт / R2, (2) де F -сила, яка діючи на тіло, надає йому прискорення а. При цьому, як видно з (1), чим більша маса m тіла тим меншого прискорення набуває тіло. Тобто у даному випадку маса характеризує інерційні властивості тіла, є його мірою інерції (інертною масою). Згідно з законом всесвітнього тяжіння: Fт = γ mт Mт / R2, (3) де: Fт – сила тяжіння, γ - гравітаційна стала, R відстань між тілами; mт , Mт - маси тяжіння. У цьому випадку маса тіла mт характеризує його властивість притягуватись до іншого (наприклад до Землі). Таким чином маси mт і m виражають різні властивості тіла і тому в принципі можуть бути нерівні і непропорційні. Тому й виникає потреба у порівнянні цих мас. Для цього розглянемо проявлення сил (1) та (2) в двох системах – інерціальній та неінерціальній, що рухається з прискоренням відносно першої. Хай інерціальна система координат зв’язана з поверхнею Землі, а неінерціальна - з вагоном, що рухається по закругленню радіуса r. При русі вагона зі швидкістю v підвішене до його стелі тіло відхилиться від вертикалі на деякий кут α (рис. 1). В неінерціальній системі координат це відхилення зумовлено дією доцентрової сили F = m a = mv2 / r, яка діє через підвіс і надає тілу прискорення, примушуючи його рухатися по колу. В неінерціальній системі вагона спостерігач, не знаючи нічого про рух вагона, робить висновок про те, що причиною відхилення є деяка горизонтальна сила інерції, протилежна доцентровій: Fi = mv2 / r. (3)
де h - висота підняття головки маятника дорівнює h = R(1 – cosα), де R - відстань від осі обертання до її центру ваги.


Досліди, що виконуються із все зростаючою точністю, показують, що відношення цих мас відрізняється від одиниці в одинадцятому знакові після дробової коми. Це серйозна підстава вважати, що m і mт є проявленням однієї і тієї ж величини. Ця обставина була використана А. Ейнштейном як одне із обгрунтувань розробки теорії тяжіння в загальній теорії відносності. Завдання даної лабораторної роботи є перевірка рівності m/mт=1 на відцентровій машині з двома тілами однакової маси. При обертанні ротора на тіло діє відцентрова сила інерції - F = mv2 / r = ω2 r, (5) де кутову швидкість ω ми виразимо через число обертів n ротора, за хвилину ω = 2πn / 60 = πn /30 (6) З рис. 1 випливає, що r = L sin α (7) Підставляючи (6) і (7) в (5), одержимо: F = m π2 n2 L sin (α) / 900 (8) Знайдемо відношення сил (4) і (9):
На рис. 1 видно, що це відношення дорівнює ctg α, тому k = Виміріючи довжину підвісу L до центру тіл, число обертів n і кут відхилення α, за (9) можна обчислити відношення інерційної і тяжіючої мас.
Порядок виконання роботи:
1. Познайомитися з установкою, градусною шкалою, зі шкалою тахометра. 2. Опустити тягарі і стрілки в нижнє положення, ввімкнути автотрансформатор в мережу і поступово підвищуючи напругу, надати роторові обертання, при якому стрілки підіймуться на 35-50˚. 3. Дочекавшись рівномірного обертання ротора, помітити показання тахометра і вимкнути мережу. Після повної зупинки ротора записати кути відхилення усіх чотирьох стрілок з точністью до 30/ і занести їх до таблиці. 4. Виконати вимірювання за пп. 2-3 ще два рази, кожний раз трохи збільшуючи число обертів. 5. Для кожного вимірювання визначити середній по 4 –х відліках кут α і за (9) обчислити k. 6. Знайти довірчий інтервал визначення k для надійності 0,7. 7. Результати вимірювань і розрахунків записати в таблиці. Кінцевий результат записати у вигляді k = < k > ± Δk. Подати приклад розрахунків у таблиці:
Дайте відповіді на запитання: 1. Відтворіть рис. 1 за описанням його в тексті теорії. 2. Чи є інерціальною система, зв’язана з поверхнею Землі? 3. Необхідна умова для повороту велосипеда, вагона, машин, що рухаються. Що потрібно, аби всі вони не перекинулися на повороті?
Лабораторна робота № 10.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 290; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.006 с.) |



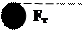



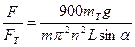
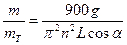 (9)
(9)


