Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Логические элементы компьютераСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Логический элемент компьютера - это часть электронной логичеcкой схемы, которая реализует элементарную логическую функцию. Логическими элементами компьютеров являются электронные схемы И, ИЛИ, НЕ, И-НЕ, ИЛИ-НЕ и другие (называемые также вентилями), а также триггер. С помощью этих схем можно реализовать любую логическую функцию, описывающую работу устройств компьютера. Обычно у вентилей бывает от двух до восьми входов и один или два выхода. Чтобы представить два логических состояния - "1" и "0" в вентилях, соответствующие им входные и выходные сигналы имеют один из двух установленных уровней напряжения. Например, +5 вольт и 0 вольт. Высокий уровень обычно соответствует значению "истина" ("1"), а низкий - значению "ложь" ("0"). Каждый логический элемент имеет свое условное обозначение, которое выражает его логическую функцию, но не указывает на то, какая именно электронная схема в нем реализована. Это упрощает запись и понимание сложных логических схем. Работу логических элементов описывают с помощью таблиц истинности. Таблица истинности - это табличное представление логической схемы (операции), в котором перечислены все возможные сочетания значений истинности входных сигналов (операндов) вместе со значением истинности выходного сигнала (результата операции) для каждого из этих сочетаний. Логические схемы С х е м а И Схема И реализует конъюнкцию двух или более логических значений. Условное обозначение на структурных схемах схемы И с двумя входами представлено на рис. 2.1. Таблица истинности - в таблице 2.1.
Единица на выходе схемы И будет тогда и только тогда, когда на всех входах будут единицы. Когда хотя бы на одном входе будет ноль, на выходе также будет ноль. Связь между выходом z этой схемы и входами x и y описывается соотношением: z = xy (читается как " x и y"). Операция конъюнкции на функциональных схемах обозначается знаком "&" (читается как "амперсэнд"), являющимся сокращенной записью английского слова and.
С х е м а ИЛИ Схема ИЛИ реализует дизъюнкцию двух или более логических значений. Когда хотя бы на одном входе схемы ИЛИ будет единица, на её выходе также будет единица. Условное обозначение схемы ИЛИ представлено на рис. 2.2. Знак "1" на схеме - от устаревшего обозначения дизъюнкции как ">=1" (т.е. значение дизъюнкции равно единице, если сумма значений операндов больше или равна 1). Связь между выходом z этой схемы и входами x и y описывается соотношением: z = x v y (читается как " x или y "). Таблица истинности - в табл. 2.2.
С х е м а НЕ Схема НЕ (инвертор) реализует операцию отрицания. Связь между входом x этой схемы и выходом z можно записать соотношением z = Если на входе схемы 0, то на выходе 1. Когда на входе 1, на выходе 0. Условное обозначение инвертора - на рисунке 2.3, а таблица истинности - в табл. 2.3.
С х е м а И - НЕ Схема И-НЕ состоит из элемента И и инвертора и осуществляет отрицание результата схемы И. Связь между выходом z и входами x и y схемы записывают следующим образом: Условное обозначение схемы И-НЕ представлено на рисунке 2.4. Таблица истинности схемы И-НЕ - в табл. 2.4.
С х е м а ИЛИ -НЕ Схема ИЛИ-НЕ состоит из элемента ИЛИ и инвертора и осуществляет отрицание результата схемы ИЛИ. Связь между выходом z и входами x и y схемы записывают следующим образом:
Двоичный сумматор Сумматор - это электронная логическая схема, выполняющая суммирование двоичных чисел. Сумматор служит, прежде всего, центральным узлом арифметико-логического устройства компьютера, однако он находит применение также и в других устройствах машины. Многоразрядный двоичный сумматор, предназначенный для сложения многоразрядных двоичных чисел, представляет собой комбинацию одноразрядных сумматоров, с рассмотрения которых мы и начнём. Условное обозначение одноразрядного сумматора на рис. 2.6.
Рис. 2.6
При сложении чисел A и B в одном i -ом разряде приходится иметь дело с тремя цифрами: 1. цифра a i первого слагаемого; 2. цифра b i второго слагаемого; 3. перенос p i-1 из младшего разряда. В результате сложения получаются две цифры: 1. цифра c i для суммы; 2. перенос p i из данного разряда в старший. Таким образом, одноразрядный двоичный сумматор есть устройство с тремя входами и двумя выходами, работа которого может быть описана следующей таблицей истинности:
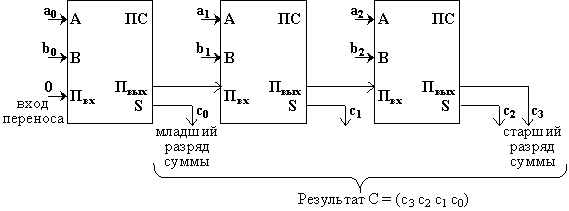
Если требуется складывать двоичные слова длиной два и более бит, то можно использовать последовательное соединение таких сумматоров, причём для двух соседних сумматоров выход переноса одного сумматора является входом для другого. Например, схема вычисления суммы C = (с3 c2 c1 c0) двух двоичных трехразрядных чисел A = (a2 a1 a0) и B = (b2 b1 b0) может иметь вид:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 462; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.178.145 (0.01 с.) |

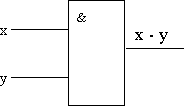 Рис. 2.1
Рис. 2.1
 Рис. 2.2
Рис. 2.2
 , где
, где  Рис. 2.3
Рис. 2.3
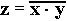 , где
, где 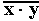 читается как " инверсия x и y ".
читается как " инверсия x и y ".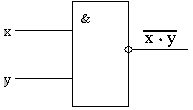 Рис. 2.4
Рис. 2.4
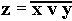 , где
, где 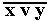 , читается как " инверсия x или y ". Условное обозначение схемы ИЛИ-НЕ представлено на рис. 2.5. Таблица истинности схемы ИЛИ-НЕ - в табл. 2.5.
, читается как " инверсия x или y ". Условное обозначение схемы ИЛИ-НЕ представлено на рис. 2.5. Таблица истинности схемы ИЛИ-НЕ - в табл. 2.5.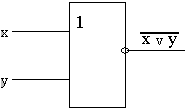 Рис. 2.5
Рис. 2.5