
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Порядок проведення експериментівСодержание книги
Поиск на нашем сайте 1. Відкрити кран 10 і наповнити бак 1 водою до верхньої позначки на водомірному склі 2. 2. Відкрити затискач 8 та пустити забарвлену рідину в скляну трубу 3. Відрегулювати витрату води в трубі 3 за допомогою крана 4 таким чином, щоб забарвлена рідина, що надходить з капілярної трубки 7, набула вигляду чіткої прямої струминки, спрямованої вздовж осі труби. При цьому необхідно слідкувати за підтриманням сталого рівня води в баці 1, регулюючи кран 10. 3. Визначити витрату води у трубі 3, вимірюючи час заповнення мірної ємності 5. Занести це значення та результат візуального спостереження за струминкою у таблицю 4.1. 4. Виміряти температуру води, що тече по трубі 3 та, в залежності від цієї температури, визначити відповідні коефіцієнт динамічної в’язкості (див. додаток) та густину води (яку приблизно можна прийняти рівною ρ =1000 кг/м3). Дані занести в таблицю 4.1. 5. Провести ще декілька дослідів, змінюючи витрату води в трубці 3 за допомогою крана 4 кожного разу таким чином, щоб забарвлена струминка спочатку набула хвилястих обрисів, а потім (в останньому досліді) одразу після виходу з капілярної трубки 7 повністю розмилася. Під час дослідів підтримувати сталий рівень води в баці 1, регулюючи кран 10. Заміряти час наповнення мірної ємності 5 в кожному досліді. Дані замірів та візуальних спостережень за поведінкою забарвленої струминки рідини занести в таблицю 4.1. Таблиця 4.1. Результати експериментів
Порядок обробки результатів експерименту 1. Визначити витрату води Q [м3/с]у скляній трубці 3 у кожному досліді за формулою
де V=0,002 м3 – об’єм мірної ємності, τ – час її заповнення, с. Дані розрахунків занести у таблицю 4.2. 2. Обчислити середню швидкість руху води в скляній трубці 3 у кожному досліді за формулою: Дані розрахунків занести в таблицю 4.2. 3. Для кожного досліду розрахувати число Рейнольдса за формулою:
Дані розрахунків занести в таблицю 4.2. 4. Визначити режим течії рідини відповідно до значень числа Рейнольдса в кожному досліді, занести результати визначення в таблицю 4.2. Зіставити дані візуальних спостережень з розрахунковими даними. Таблиця 4.2. Результати розрахунків
4.6. Контрольні запитання 1. Які існують режими руху рідини, в чому полягає різниця між ними? 2. Від яких параметрів залежить режим руху рідини? 3. Що характеризує число Рейнольдса, його фізичний зміст, за якою формулою воно розраховується? 4. Що називається еквівалентним діаметром? 5. Чому дорівнює критичне число Рейнольдса? 6. Розподілення швидкостей у перерізі труби при ламінарному та турбулентному русі. Яке співвідношення між середньою та максимальною швидкостями потоку при цих двох режимах руху рідини? 7. Яким чином можна змінювати число Рейнольдса в даній роботі? 8. Яке рівняння гідравліки застосовується для підрахування швидкості руху рідини в трубопроводі? 9. Чому під час проведення експерименту необхідно підтримувати постійний рівень води в баці?
ЛАБОРАТОРНА РОБОТА № 5 ВИЗНАЧЕННЯ ВТРАТ НАПОРУ В ТРУБОПРОВОДІ Мета роботи Експериментальним шляхом визначити втрати напору в трубопроводі та порівняти експериментальні значення з теоретичними.
Теоретичні відомості Рівняння Бернуллі для двох перерізів потоку реальної рідини має вигляд:
де z1, z2 – геометрична висота або питома потенційна енергія положення, відповідно, в перерізах 1 та 2, м; Член рівняння hвтр - це загальні втрати напору на ділянці між перерізами потоку 1 та 2. Причиною втрат напору є різного роду гідравлічні опори. Опори характеризуються в’язкісними або інерційними силами. Перші залежать від внутрішнього тертя між частинками рідини, яка рухається, а другі – від здатності рідини чинити опір при русі. Загальні втрати напору складаються з лінійних втрат напору (втрат напору по довжині) hl та втрат напору на місцевих опорах hM. Лінійні втрати напору виявляються при русі реальної рідини по всій довжині трубопроводу. Втрати напору на місцевих опорах виникають при будь-яких змінах напрямку руху потоку або раптових змінах його швидкості. Втрати напору по довжині. Втрати напору по довжині можна визначити за формулою Дарсі – Вейсбаха:
де l – довжина ділянки трубопроводу, на якій визначаються втрати, м; υ – середня швидкість потоку рідини, м/с; d – внутрішній діаметр труби, м; g=9,81 м/с2 – прискорення вільного падіння; λ – гідравлічний коефіцієнт тертя. Гідравлічний коефіцієнт тертя λ в загальному випадку залежить від числа Рейнольдcа Re (тобто від режиму руху рідини) і від відношення шорсткості стінок трубопроводу Δ до діаметра труби d (або до радіуса r), тобто від відносної шорсткості. Характер впливу цих параметрів на гідравлічний коефіцієнт тертя λ видно з графіка (рис. 5.1), який є результатом дослідів І.І. Нікурадзе. І.І. Нікурадзе випробував на опір ряд труб зі штучно створеною шорсткістю на їх внутрішній поверхні. Шорсткість була отримана шляхом наклеювання певного розміру піщинок, одержаних внаслідок просіювання піску через спеціальні сита. Таким чином була отримана рівномірно розподілена зерниста шорсткість. Досліди було проведено в широкому діапазоні відносних шорсткостей (Δ / r =1/500…1/15), а також чисел Re (Re =500…106). Результати цих дослідів наведені у вигляді логарифмічних залежностей lg(100λ) від lgRe для ряду Δ / r.
Рис.5.1. Графік І. Нікурадзе (залежність lg(100λ) від lg(Re) для труб зі штучною шорсткістю): 1 – лінія ламінарного руху; 2 – лінія турбулентного руху в гідравлічно гладких трубах; А – доквадратична область змішаного тертя при турбулентному русі; 3 - умовна пряма, що поділяє області А та Б; Б – квадратична (або автомодельна) область при турбулентному русі; r – радіус труби; Δ- абсолютна рівнозерниста шорсткість.
В області ламінарного режиму (тобто при Re<2300, або lgRe<3,36) всі дослідні точки на графіку І. Нікурадзе розташувались на одній прямій 1 в лівій частині графіка. Тобто при ламінарному режимі течії коефіцієнт λ залежить тільки від числа Рейнольдcа, та не залежить від шорсткості. При значеннях числа Рейнольдcа від 2300 до 4000 (перехідна область від ламінарного режиму до турбулентного) дослідні точки розташовані між прямими 1 і 2 на рис. 5.1, коефіцієнт λ швидко зростає зі збільшенням числа Рейнольдса, але також не залежить від шорсткості. При турбулентному режимі (тобто при Re> 4000, або lgRe> 3,6) можна розрізнити три області: область гідравлічно гладких труб, доквадратичну область змішаного тертя та квадратичну (або автомодельну) область. Область гідравлічно гладких труб при турбулентному режимі знаходиться у межах 4000 <Re< 20 d/ Δ (дослідні точки в цьому інтервалі Re розташовуються вздовж нахиленої прямої 2, відомої під назвою прямої Блазіуса для гладких труб, рис. 5.1). У цій зоні утворюється такий пристінний в’язкий шар рідини, який вкриває всі виступи шорcткості. Пристінний шар утворює гідравлічно гладку поверхню, по якій турбулентне ядро потоку тече, як по вирівняній поверхні. Тому й труби в цій області називають гідравлічно гладкими. Відхилення від прямої Блазіуса настає тим швидше при збільшенні числа Рейнольдcа, чим більша шорсткість стінок. При 20 d/ Δ <Re< 500 d/ Δіснує доквадратична область змішаного тертя при турбулентному режимі (область А між лініями 2 та 3 на рис. 5.1). В цій області коефіцієнт λ залежить як від числа Рейнольдса, так і від шорсткості поверхні труби (стінок русла). В цій області величина виступів шорсткості Δмає той самий порядок, що й товщина пристінного в’язкого шару (товщина пристінного в’язкого шару рідини зменшується зі зростанням числа Re). В цій зоні починають гальмувати потік лише великі виступи, а малі та основи великих залишаються вкритими пристінним шаром і в руйнуванні потоку участі не беруть. Справа за умовною прямою 3 всі залежності йдуть паралельно осі абсцис (область Б на рис. 5.1), тобто коефіцієнт λ від числа Рейнольдcа не залежить, а залежить лише від шорсткості. Чим більша шорсткість, тим є більшим коефіцієнт λ. Ця область називається автомодельною або квадратичною. В цій зоні виступи шорсткості Δ значно перевищують товщину пристінного в’язкого шару рідини. Із вищенаведеного випливає, що одна й та сама труба може бути як гідравлічно гладкою, так і гідравлічно шорсткою, в залежності від значення числа Re. Досліди І.І.Нікурадзе проводилися на трубах зі штучною рівномірно розподіленою зернистою шорсткістю. Для промислових труб із природною нерівномірною шорсткістю закон залежності λ від Re дещо відрізняється від кривих, наведених на графіку І.І. Нікурадзе, а саме: в доквадратичній зоні змішаного тертя коефіцієнт λ виявляється завжди більшим, ніж у квадратичній (а не меншим, як у Нікурадзе для штучної шорсткості) і безперервно зменшується при переході із доквадратичної до квадратичної зони (рис. 5.2). Відмінності в кривих, наведених на рис.5.1 та 5.2, пояснюються тим, що в реальній трубі нерівності шорсткості мають різну висоту і при збільшенні числа Re починають виступати за межі в’язкого підшарку не одночасно, а при різних Re. Внаслідок цього перехід від лінії, що відповідає гладким трубам, до горизонтальних прямих, що відповідають квадратичному закону, відбувається для натуральних труб більш плавно, без провалин кривих, характерних для графіка І.І. Нікурадзе.
Рис. 5.2. Залежність коефіцієнта λ від числа Reдля труб із природною шорсткістю (за даними Всесоюзного теплотехнічного інституту):
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 356; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.011 с.) |

 ,
, , де S – площа поперечного перерізу отвору в трубі, м2, d=0,019 м - внутрішній діаметр труби.
, де S – площа поперечного перерізу отвору в трубі, м2, d=0,019 м - внутрішній діаметр труби. .
. , (5.1)
, (5.1)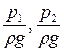 - п’єзометрична висота або питома потенційна енергія тиску в перерізах 1 та 2, м;
- п’єзометрична висота або питома потенційна енергія тиску в перерізах 1 та 2, м;  - швидкісна висота (швидкісний напір) або питома кінетична енергія потоку в перерізах 1 та 2, м; α1 та α2 – коефіцієнти Коріоліса (для ламінарного режиму течії α =2, а для турбулентного – α =1,05 – 1,1)
- швидкісна висота (швидкісний напір) або питома кінетична енергія потоку в перерізах 1 та 2, м; α1 та α2 – коефіцієнти Коріоліса (для ламінарного режиму течії α =2, а для турбулентного – α =1,05 – 1,1) , (5.2)
, (5.2)




