
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Порядок виконання експериментуСтр 1 из 6Следующая ⇒
ЛАБОРАТОРНА РОБОТА №1 ЗАКОН ПАСКАЛЯ ТА ЙОГО ЗАСТОСУВАННЯ В ТЕХНІЦІ Мета роботи Засвоїти закон Паскаля та ознайомитися із прикладами застосування цього закону у гідравлічних системах.
Теоретичні відомості Розглянемо основне рівняння гідростатики: На законі Паскаля засновано принцип дії багатьох гідравлічних пристроїв, наприклад, гідравлічного пресу, гідроакумулятора, гідравлічного домкрата. Розглянемо цей закон для гідравлічної системи (рис. 1.2). Поршень циліндра, рухаючись під дією рідини, що подається насосом, долає зовнішню силу F. Це та сила, яка прикладена до замкненого об’єму рідини (у порожнині циліндра, трубопроводах, порожнині розподільника, нагнітальній порожнині насоса). Тиск під поршнем, наприклад, у точці А дорівнює:
де S – площа поршня. Згідно закону Паскаля цей тиск передається всім точкам замкненого об’єму. Таким чином, тиск у циліндрі та трубопроводах, а також тиск, створюваний насосом, залежить від сили F: чим більша ця сила, тим більшим буде тиск у системі й навпаки. Отже, тиск, створений насосом, залежить від зовнішніх сил, прикладених до рідини. У загальному випадку до зовнішніх сил відносяться корисні сили, всі сили тертя, як у направляючих машин, так і в робочому циліндрі, а також сили тертя, що виникають між частинками рідини під час її руху по трубах (втрати напору). Тиск на виході з насоса в перерізі 0 –0 більше за тиск у точці А на величину гідростатичного тиску, зумовленого стовпом рідини h та втратами напору в трубах.
Опис лабораторної установки
Лабораторна установка (рис.1.2) - це найпростіша гідравлічна система, яка складається з бака 1, де знаходиться робоча рідина, насоса 2, запобіжного клапана 3, двопозиційного розподільника 4 кранового типу, робочого циліндра двосторонньої дії 5, трубопроводів. З нагнітальною магістраллю з’єднаний манометр 6 для вимірювання тиску в системі, зі штоком 8 циліндра – площина (підвіска), на яку можна підвішувати вантажі різної маси. При роботі системи поршень 7 робочого циліндра переміщується вверх або вниз, залежно від положення розподільника 4.
Порядок виконання експерименту 1. Увімкнути установку. 2. За допомогою розподільника задати напрям руху поршня (наприклад, уверх). За допомогою манометра визначити тиск, що виникає в гідравлічній системі без розміщення вантажів на підвісці. 3. За допомогою розподільника змінити напрям руху і знову визначити тиск у гідравлічній системі. 4. Повторити заміри за пп. 2 і 3, розміщуючи на підвісці вантажі різної маси. 5. Визначити тиск, на який відрегульовано запобіжний клапан. Занести результати вимірів у таблицю 1.1.
Таблиця 1.1. Результати вимірів
Примітка. 1 кгс/см2=98100 Па. Таблиця 1.2. Результати розрахунків
1.6. Контрольні питання 1. В чому полягає суть закону Паскаля? 2. Як реалізується закон Паскаля в гідравлічній системі? 3. Від чого залежить тиск, створений насосом? 4. Для чого в системі використовується запобіжний клапан?
5. Який тиск встановлюється в системі, коли спрацьовує запобіжний клапан? 6. Чи буде однаковим тиск у нагнітальній камері насоса та в робочій порожнині силового циліндра? 7. Які сили заважають рухові поршня в силовому циліндрі?
ЛАБОРАТОРНА РОБОТА № 2 ЗІ СТАЛОЮ КУТОВОЮ ШВИДКІСТЮ Ціль роботи Визначити з досліду форму вільної поверхні рідини в циліндричній посудині, що обертається відносно вертикальної осі зі сталою кутовою швидкістю, та порівняти дослідні дані з теоретичними.
Теоретичні відомості Випадок відносного спокою рідини в посудинах, що обертаються зі сталою кутовою швидкістю ω навколо вертикальної осі, часто зустрічається на практиці (наприклад, у сепараторах та центрифугах, що застосовуються для розподілення рідин). При цьому (рис. 2.1) на кожну частинку рідини масою dm при її відносному спокої діють масові сили: сила тяжіння dG=dm∙g та сила інерції dFін=dm∙ω2r, де r – відстань частинки рідини від осі обертання ( Проекції прискорень цих сил на осі координат дорівнюють:
Спочатку знайдемо закон розподілення тиску в рідині, що знаходиться у відносному спокої. Такий закон можна знайти шляхом інтегрування диференціального рівняння рівноваги рідини:
де dp – повний диференціал тиску; ρ – густина рідини; X, Y, Z – проекції на координатні осі x, y, z прискорень масових сил, що діють на будь – яку частинку рідини. Підставивши в рівняння (2.2) відповідні проекції прискорень масових сил з виразів (2.1), отримуємо рівняння:
Звідки після інтегрування знаходимо:
Сталу інтегрування знаходимо при умові, що при z=z0 та x=y= 0 тиск дорівнює тиску на вільній поверхні рідини: р=р0 (якщо посудина відкрита, тоді тиск в цій точці дорівнює атмосферному: р=ра). Отже, C=p0+ρgz0. Підставляючи це значення в рівняння (2.4) та враховуючи, що r2=x2+y2, отримуємо закон розподілення тиску:
Цьому рівнянню можна надати форми основного рівняння гідростатики:
де Рівняння (2.6) показує, що в даному випадку розподілення тиску підпорядковується лінійному закону для будь – якої фіксованої круглоциліндричної поверхні. Тепер визначимо рівняння, що описує форму поверхні рівного тиску та вільної поверхні. Нагадаємо, що поверхнею рівного тиску називається поверхня, тиск у всіх точках якої є однаковим, а вільною поверхнею рідини називається поверхня, що межує з газовим середовищем (повітрям). На вільну поверхню діє зовнішній тиск р0, який у всіх її точках є однаковим, – це окремий випадок поверхні рівного тиску. У відкритому резервуарі на вільну поверхню діє атмосферний тиск ра. Оскільки для поверхні рівного тиску p=const, тоді dp= 0 і рівняння (2.2) набуває вигляду:
Підставивши в це рівняння замість X, Y та Z їх вирази з (2.1), після інтегрування отримуємо рівняння поверхонь рівного тиску:
де С – стала інтегрування. Поверхні рівного тиску, в тому числі й вільна поверхня, що описуються рівнянням (2.8), являють собою параболоїди обертання відносно вертикальної осі z, які при перетині вертикальними площинами дають параболи, а при перетині горизонтальними площинами – кола. Таким чином, при обертанні посудини з рідиною зі сталою кутовою швидкістю ω навколо вертикальної осі поверхнями рівного тиску буде сімейство параболоїдів обертання.
Сталу інтегрування С в рівнянні (2.8) для вільної поверхнівизначимо з умови, що при x=y=0 z=z0, відповідно C= -gz0. Тоді рівняння, що описує форму вільної поверхні, набуває вигляду:
де z0 – вертикальна координата вершини параболоїда вільної поверхні; r, z – координати будь – якої точки вільної поверхні. Якщо розташувати початок координат у вершині параболоїда вільної поверхні (z0 =0), тоді рівняння вільної поверхні спрощується:
З рівняння (2.10) видно, що форма вільної поверхні не залежить від густини рідини, а визначається лише кутовою швидкістю ω.
Схема лабораторної установки наведена на рис. 2.2. Установка складається з циліндричної посудини 1, що обертається. Посудина 1 заповнена рідиною. Для визначення форми вільної поверхні рідини призначені вертикальна 3 та горизонтальна 4 шкали координатометра з вимірювальною голкою 2. Вимірювальна голка 2 переміщується вертикально за допомогою рукоятки 5, а горизонтально – за допомогою рукоятки 6. Прилад включається за допомогою тумблера 7. Для встановлення необхідної частоти обертання циліндру слугує регулятор 8. Частоту обертання визначають за допомогою індикатора 9. Таблиця 2.1. Координати вільної поверхні рідини та результати розрахунків
Таблиця 2.2. Вихідні значення та результати розрахунків
2.6. Контрольні питання
1. Чи може рідина, що рухається, знаходитися в рівновазі? Якщо може, тоді за яких умов? 2. Дати визначення поверхні рівного тиску та вільної поверхні. 3. Якої форми набуває вільна поверхня рідини (або будь – яка інша поверхня рівного тиску) в посудині, що обертається навколо вертикальної осі зі сталою кутовою швидкістю? Чи залежить форма вільної поверхні від густини рідини? 4. Чи справедливе основне рівняння гідростатики для різних випадків відносного спокою рідини?
ЛАБОРАТОРНА РОБОТА № 3 ІЛЮСТРАЦІЯ РІВНЯННЯ БЕРНУЛЛІ ПРИ УСТАЛЕНІЙ ТЕЧІЇ РІДИНИ В НАПІРНОМУ ТРУБОПРОВОДІ Мета роботи Дослідним шляхом перевірити справедливість рівняння Бернуллі: зменшення повної енергії потоку при русі реальної рідини, перехід потенційної енергії в кінетичну й, навпаки, при русі в трубі зі змінним перерізом. Теоретичні відомості Рівняння Бернуллі є основним рівнянням гідродинаміки і встановлює зв’язок між трьома складовими енергії рухомої рідини – енергією положення, енергією тиску й кінетичною енергією. Розглянемо спочатку струминку ідеальної рідини. Візьмемо два будь – які поперечні перерізи цієї струминки: 1 та 2. Швидкості рідини υ1 та υ2 у всіх точках відповідних перерізів для елементарної струминки є однаковими. Рівняння Бернуллідля двох перерізів струминки ідеальної (нев’язкої) рідини має вигляд:
Складові, що входять в рівняння (3.1), можна інтерпретувати з геометричної та енергетичної точок зору наступним чином. З геометричної точки зору (рис. 3.1): z – геометрична висота, м – відстань від довільної площини порівняння до центру тяжіння відповідного живого перерізу; Із гідростатики відомо, що вираз Для елементарної струминки ідеальної рідини
З енергетичної точки зору:
z – питома (віднесена до одиниці ваги рідини) потенційна енергія положення для відповідного перерізу струминки;
Рівняння (3.1) виражає закон збереження механічної енергії для струминки ідеальної рідини. Тепер розглянемо струминку реальної (в’язкої) рідини. На шляху руху струминки в’язкої рідини виникають різного роду гідравлічні опори (наприклад, опори сил гідравлічного тертя). Позначивши втрату напору hвтр, що витрачається на подолання сил гідравлічних опорів між перерізами, запишемо рівняння Бернуллі для струминки реальної рідини:
Потік реальної рідини складається з множини елементарних струминок. Щоб поширити на потік реальної рідини рівняння Бернуллі, одержане для елементарної струминки реальної рідини, необхідно записати його для великої кількості струминок, що складають потік, а потім їх скласти. Швидкості руху елементарних струминок в потоці різні, тому й кінетична енергія струминок різна. Якщо кінетичну енергію потоку виразити через середню швидкість υс і порівняти її із сумою кінетичних енергій елементарних струминок, то виявиться, що вона менша за останню. Тому у величину кінетичної енергії, визначену за середньою швидкістю, вводять коефіцієнт α (коефіцієнт Коріоліса), який дорівнює відношенню дійсної кінетичної енергії потоку в даному перерізі до кінетичної енергії, обчисленої за середньою швидкістю. Величина α залежить від епюри розподілення швидкості по перерізу потоку та режиму руху. Для ламінарного режиму руху – α =2. Для турбулентного режиму руху α =1,05...1,1, а для більшості практичних розрахунків для цього режиму можна прийняти α= 1. Рівняння Бернуллі для потоку в’язкої рідини має вигляд:
де υс1 та υс2 – середні швидкості в перерізах, що розглядаються (зазвичай індекс «с» не наводять); Якщо для струминки ідеальної рідини рівняння Бернуллі являє собою закон збереження механічної енергії, то для потоку реальної рідини воно є рівнянням балансу енергій з урахуванням втрат. Енергія, що втрачається на даній ділянці течії (hвтр), перетворюється на теплову. Як вже було зазначено вище, всі члени рівняння Бернуллі мають лінійну розмірність, що дає можливість представляти його у вигляді графіку, що називається діаграмою рівняння Бернуллі (рис. 3.2). Розглянемо течію реальної рідини в каналі зі змінним перерізом. На рис. 3.2 показано відрізки вертикальних прямих, що відповідають кожній зі складових рівняння Бернуллі для трьох довільно обраних перерізів. При цьому z – вертикальна відстань від довільно обраної площини порівняння до центру тяжіння відповідного перерізу (геометрична висота); р/(ρg) – п’єзометрична висота; αυ2/(ρg) – швидкісна висота (швидкісний напір). Сума трьох висот, як зазначено вище, називається повним напором. Лінія, що з’єднує відмітки гідродинамічних або повних напорів Звуження потоку призводить до збільшення швидкості течії та, відповідно, швидкісного напору і до зменшення п’єзометричної висоти. На ділянці звуження п’єзометрична лінія знижується. Розширення потоку призводить до зворотного ефекту – п’єзометрична висота збільшується, а п’єзометрична лінія піднімається.
Рис. 3.2. Діаграма рівняння Бернуллі (геометрична інтерпретація) для потоку реальної рідини.
Замірявши різницю висот підйому Δ h рідини в трубці Піто та п’єзометрі, легко визначити швидкість рідини в даній точці: При розв’язуванні практичних задач за допомогою рівняння Бернуллі необхідно враховувати наступні вимоги. Рівняння Бернуллі справедливе лише для усталеного руху рідини і його можна застосовувати для тих живих перерізів потоку, в яких виконується умова повільно змінного руху, тобто коли кут розбіжності ліній течії та їх кривизна є незначними.
Опис лабораторної установки Основною частиною лабораторної установки (рис. 3.4) є закріплений на панелі похилий трубопровід зі змінним перерізом 1. Робоча рідина надходить до трубопроводу з напірного бака 2, куди вона нагнітається відцентровим насосом 3 з резервуара 4 через кран 9. Для забезпечення усталеної течії рідини в трубопроводі рівень води в напірному баці 2 підтримується сталим за допомогою зливної трубки 5. Витрата рідини в трубопроводі 1 регулюється краном 6. Через нього також відбувається злив робочої рідини до резервуара 4, що слугує одночасно основою установки. По довжині трубопроводу виділено п’ять характерних ділянок, що розрізняються за формою та розмірами поперечного перерізу. В кожному з цих перерізів встановлено по дві трубки: ліва – п’єзометрична трубка 7 та права – трубка Піто 8. Трубки змонтовані на панелі установки та мають шкали для визначення рівня підйому рідини в них. Для визначення геометричної висоти центрів виділених перерізів встановлені лінійки. При цьому за площину порівняння приймається площина кришки резервуара 4. Для візуального спостереження за потоком рідини, що тече по трубопроводу, його стінки виконані з органічного скла. Включення відцентрового насоса здійснюється тумблером, що знаходиться на панелі установки.
Порядок виконання роботи 1. Перед проведенням досліду закрити кран 6. 2. За допомогою тумблера увімкнути насос 3 та заповнити напірний бак 2 рідиною до заданого рівня. Насос залишається в робочому стані протягом досліду. Надлишок рідини у напірному баці 2 переливається до зливної трубки 5, забезпечуючи стабільний напір. 3. Відкриттям крану 6 встановити бажаний режим роботи установки (відповідну витрату рідини). При проведенні досліду необхідно слідкувати за тим, щоб у баці 2 напір рідини залишався незмінним. 4. У кожному із п’яти перерізів трубопроводу визначити геометричну висоту zi, п’єзометричну висоту Pi / (ρg), а також показання трубки Піто - Pi /(ρg) + υi 2/(2g). Результати вимірів занести до таблиці 3.1. 5. Змінити витрату рідини за допомогою крану 6 у бік збільшення або зменшення. 6. Для нового значення витрати рідини виконати вимірювання у послідовності, наведеній у п. 4, і результати вимірів занести до таблиці 3.1.
Рис. 3.4. Схема лабораторної установки: 1 – трубопровід зі змінним перерізом; 2 – напірний бак; 3 – відцентровий насос; Таблиця 3.1. Результати вимірів та розрахунків
Мета роботи Дослідження режимів течії рідини за візуальними спостереженнями та з підрахунком числа Рейнольдса.
Теоретичні відомості При течії рідини режим її руху може бути ламінарнимабо турбулентним. При ламінарному режимі руху частинки рідини рухаються шарами, паралельно один одному без перемішування, рух має упорядкований характер.Струминки рідини мають різні швидкості, але швидкість кожної струминки є сталою та спрямованою вздовж потоку. При турбулентному русі частинки рідини рухаються з великими швидкостями в різних напрямках. Рух носить неупорядкований характер, при цьому частинки рухаються як в осьовому, так і радіальному напрямках. В кожній точці потоку відбуваються швидкі зміни швидкості в часі – так звані пульсації швидкості. Однак значення миттєвих швидкостей коливаються відносно деякої середньої швидкості. Два різних режими руху рідини та можливість взаємного переходу одного режиму до іншого можна спостерігати, пропускаючи по скляній трубі воду з різними швидкостями та вводячи по осі труби тонку струминку забарвленої рідини. При невеликих швидкостях забарвлена струминка рухається у воді прямолінійно, не перемішуючись із нею. Зі зростанням швидкості води забарвлена струминка починає набувати хвилястих обрисів, шлях її стає звивистим, але вона ще має чіткий обрис. При досягненні деякої критичної швидкості забарвлена струминка повністю руйнується, а вся маса води у скляній трубці підфарбовується, іншими словами, частинки рідини під час руху змішуються, і сам рух стає неупорядкованим. Різка зміна течії забарвленої струминки й характеризує перехід ламінарного режиму руху рідини до турбулентного. Досліди, проведені О.Рейнольдсом, показали, що характер руху рідини залежить не тільки від середньої швидкості потоку рідини, але й від діаметра труби, густини та в’язкості рідини. Перехід одного виду руху до іншого відбувається при певному значенні комплексу перелічених величин, що називається критерієм Рейнольдса:
де u – середня швидкість потоку рідини, м/с; d – діаметр труби, м; ρ – густина рідини, кг/м3; μ - коефіцієнт динамічної в’язкості рідини, Па∙с. Критерій Рейнольдса є безрозмірною величиною. Із фізичної точки зору критерій Re є відношенням сил інерції до сил в’язкості. При русі рідини в трубах або каналах не круглого перерізу у вираз критерію Рейнольдса (4.1) замість діаметра підставляють величину еквівалентного діаметра:
де S – площа поперечного перерізу потоку, м2; П – змочений периметр, м. Із виразу (4.1) випливає, що турбулентний рух виникає зі збільшенням діаметра труби, швидкості руху та густини рідини або зі зменшенням в’язкості рідини. Величина числа Re, яка відповідає переходу одного виду руху в інший, називається критичним значенням числа Рейнольдса, так для прямих труб Reкр =2320. Рух рідини в прямих трубах при Re< 2320 є ламінарним. При Re> 2320 рух є турбулентним, проте розвинутого турбулентного характеру він набуває при Re> 10000. У межах Re від 2320 до 10000 турбулентний рух є недостатньо стійким (перехідна область). Розглянемо також розподіл швидкостей у перерізі труби при ламінарному та турбулентному русі рідини (рис. 4.1).
При ламінарному русі (рис. 4.1, а) швидкість частинок рідини у перерізу труби змінюється по параболі від нуля біля стінок труби до максимуму на її осі. При цьому середня швидкість рідини дорівнює половині максимальної υ cep = 0,5 υ max. Такий розподіл швидкостей встановлюється на деякій відстані від входу до труби. При турбулентному русі (рис. 4.1, б), внаслідок перемішування рідини, розподіл швидкостей в перерізі труби є більш рівномірним, ніж при ламінарному русі, при цьому υce p = (0,8…0,9) υmax. Але й при турбулентному русі в дуже тонкому граничному шарі біля стінок рух носить ламінарний характер. Цей шар товщиною δ називається ламінарним граничним шаром. Опис лабораторної установки Установка (рис. 4.2) складається з металевого бака 1 з водомірним склом 2. До бака приєднана скляна труба 3, на якій встановлено кран 4 для регулювання швидкості руху води. Це дозволяє створювати в трубці різні режими руху рідини. Зі скляної труби 3 вода надходить до мірної ємності 5. Над металевим баком розміщена посудина 6 із забарвленою рідиною, яка подається до труби 3 по її осі через капілярну трубку 7. Регулювання надходження забарвленої рідини здійснюється за допомогою затискача 8. Перед проведенням дослідів металевий бак 1 заповнюють водою через водопровідну трубу 9 з краном 10. Рівень води у баці під час дослідів підтримують сталим, регулюючи кран 10.
Таблиця 4.1. Результати експериментів
Таблиця 4.2. Результати розрахунків
4.6. Контрольні запитання 1. Які існують режими руху рідини, в чому полягає різниця між ними? 2. Від яких параметрів залежить режим руху рідини? 3. Що характеризує число Рейнольдса, його фізичний зміст, за якою формулою воно розраховується? 4. Що називається еквівалентним діаметром? 5. Чому дорівнює критичне число Рейнольдса? 6. Розподілення швидкостей у перерізі труби при ламінарному та турбулентному русі. Яке співвідношення між середньою та максимальною швидкостями потоку при цих двох режимах руху рідини? 7. Яким чином можна змінювати число Рейнольдса в даній роботі? 8. Яке рівняння гідравліки застосовується для підрахування швидкості руху рідини в трубопроводі? 9. Чому під час проведення експерименту необхідно підтримувати постійний рівень води в баці?
ЛАБОРАТОРНА РОБОТА № 5 Мета роботи Експериментальним шляхом визначити втрати напору в трубопроводі та порівняти експериментальні значення з теоретичними.
Теоретичні відомості Рівняння Бернуллі для двох перерізів потоку реальної рідини має вигляд:
де z1, z2 – геометрична висота або питома потенційна енергія положення, відповідно, в перерізах 1 та 2, м; Член рівняння hвтр - це загальні втрати напору на ділянці між перерізами потоку 1 та 2. Причиною втрат напору є різного роду гідравлічні опори. Опори характеризуються в’язкісними або інерційними силами. Перші залежать від внутрішнього тертя між частинками рідини, яка рухається, а другі – від здатності рідини чинити опір при русі. Загальні втрати напору складаються з лінійних втрат напору (втрат напору по довжині) hl та втрат напору на місцевих опорах hM. Лінійні втрати напору виявляються при русі реальної рідини по всій довжині трубопроводу. Втрати напору на місцевих опорах виникають при будь-яких змінах напрямку руху потоку або раптових змінах його швидкості. Втрати напору по довжині. Втрати напору по довжині можна визначити за формулою Дарсі – Вейсбаха:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 582; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.102.137 (0.13 с.) |
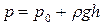
 . З нього видно, що тиск р (рис. 1.1) у будь-якій точці рідини (наприклад, у т. М), що знаходиться в рівновазі, складається з надлишкового тиску ρgh, що залежить від густини рідини ρ та глибини занурення h цієї точки відносно вільної поверхні і тиску на вільній поверхні р0 (зовнішнього тиску).Тиск на вільній поверхні автоматично, так би мовити, передається в будь-яку точку рідини. Тільки зміниться тиск на вільній поверхні, як одразу це нове значення р0 дасть про себе знати в будь-якій точці рідини. Ця властивість підтверджується законом Паскаля, який можна сформулювати так: зовнішнійтиск, що діє на рідину, передається всім частинкам цієї рідини по всім напрямкам без змін.
. З нього видно, що тиск р (рис. 1.1) у будь-якій точці рідини (наприклад, у т. М), що знаходиться в рівновазі, складається з надлишкового тиску ρgh, що залежить від густини рідини ρ та глибини занурення h цієї точки відносно вільної поверхні і тиску на вільній поверхні р0 (зовнішнього тиску).Тиск на вільній поверхні автоматично, так би мовити, передається в будь-яку точку рідини. Тільки зміниться тиск на вільній поверхні, як одразу це нове значення р0 дасть про себе знати в будь-якій точці рідини. Ця властивість підтверджується законом Паскаля, який можна сформулювати так: зовнішнійтиск, що діє на рідину, передається всім частинкам цієї рідини по всім напрямкам без змін. ,
,
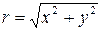 ); ω- кутова швидкість. Рівнодійною цих сил є масова сила dR, яка спрямована по нормалі до поверхні рівня.
); ω- кутова швидкість. Рівнодійною цих сил є масова сила dR, яка спрямована по нормалі до поверхні рівня.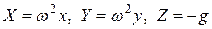 . (2.1)
. (2.1) , (2.2)
, (2.2) . (2.3)
. (2.3) . (2.4)
. (2.4) . (2.5)
. (2.5)
 , (2.6)
, (2.6)
 .
. . (2.7)
. (2.7) , (2.8)
, (2.8) , (2.9)
, (2.9)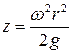 . (2.10)
. (2.10) 2.3. Опис лабораторної установки
2.3. Опис лабораторної установки , см
(g =981 см/с2)
, см
(g =981 см/с2)



 . (3.1)
. (3.1) - п’єзометрична висота, м (тобто висота такого стовпа рідини з густиною ρ, який біля своєї основи створює тиск р, що дорівнює тискові у відповідному перерізі; якщо у перерізах струминки встановити п’єзометричні трубки, тоді рідина в них підніметься на висоту р/ (ρg));
- п’єзометрична висота, м (тобто висота такого стовпа рідини з густиною ρ, який біля своєї основи створює тиск р, що дорівнює тискові у відповідному перерізі; якщо у перерізах струминки встановити п’єзометричні трубки, тоді рідина в них підніметься на висоту р/ (ρg));  - швидкісна висота або швидкісний напір, м.
- швидкісна висота або швидкісний напір, м. є п’єзометричним напором. Сума
є п’єзометричним напором. Сума 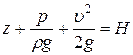 називається повним або гідродинамічним напором.
називається повним або гідродинамічним напором. Рис. 3.1. Графічне зображення членів рівняння Бернуллі для елементарної струминки ідеальної рідини.
Рис. 3.1. Графічне зображення членів рівняння Бернуллі для елементарної струминки ідеальної рідини. - питома кінетична енергія;
- питома кінетична енергія;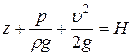 - повна питома механічна енергія.
- повна питома механічна енергія. . (3.6)
. (3.6) , (3.7)
, (3.7) - коефіцієнти Коріоліса; hвтр – втрата напору на ділянці між перерізами 1 та 2.
- коефіцієнти Коріоліса; hвтр – втрата напору на ділянці між перерізами 1 та 2.
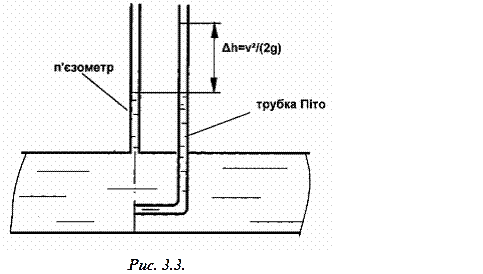 Для визначення п’єзометричної висоти використовують, як вже зазначено вище, п’єзометри. Якщо встановити в потоці трубку (трубку Піто), кінчик якої зігнутий під кутом 900 отвором назустріч потоку та п’єзометр, тоді рідина в трубці Піто підніметься над рівнем у п’єзометрі на висоту Δ h, що дорівнює швидкісному напору υ2/2g у точці заміру (рис.3.3).
Для визначення п’єзометричної висоти використовують, як вже зазначено вище, п’єзометри. Якщо встановити в потоці трубку (трубку Піто), кінчик якої зігнутий під кутом 900 отвором назустріч потоку та п’єзометр, тоді рідина в трубці Піто підніметься над рівнем у п’єзометрі на висоту Δ h, що дорівнює швидкісному напору υ2/2g у точці заміру (рис.3.3).  . Але слід пам’ятати, що таким способом визначається швидкість в даній точці рідини, а не середня швидкість у відповідному перерізі потоку, яка входить до складової швидкісного напору в рівнянні Бернуллі для потоку реальної рідини.
. Але слід пам’ятати, що таким способом визначається швидкість в даній точці рідини, а не середня швидкість у відповідному перерізі потоку, яка входить до складової швидкісного напору в рівнянні Бернуллі для потоку реальної рідини.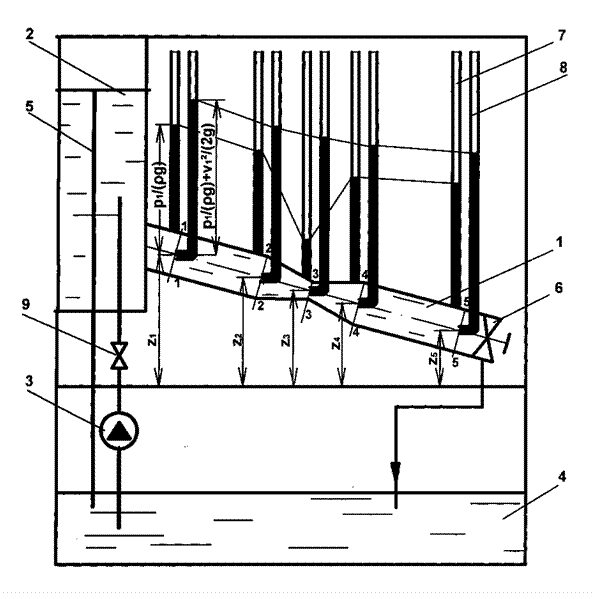
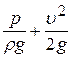 ,
см
,
см
 ,
см
,
см
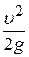 ,
см
(різниця між показанням трубки Піто та п’єзометра)
,
см
(різниця між показанням трубки Піто та п’єзометра)
 , см
, см
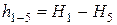 =, см
=, см
 , (4.1)
, (4.1)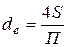 , (4.2)
, (4.2)

 , (5.1)
, (5.1)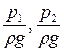 - п’єзометрична висота або питома потенційна енергія тиску в перерізах 1 та 2, м;
- п’єзометрична висота або питома потенційна енергія тиску в перерізах 1 та 2, м;  - швидкісна висота (швидкісний напір) або питома кінетична енергія потоку в перерізах 1 та 2, м; α1 та α2 – коефіцієнти Коріоліса (для ламінарного режиму течії α =2, а для турбулентного – α =1,05 – 1,1)
- швидкісна висота (швидкісний напір) або питома кінетична енергія потоку в перерізах 1 та 2, м; α1 та α2 – коефіцієнти Коріоліса (для ламінарного режиму течії α =2, а для турбулентного – α =1,05 – 1,1)


