
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Резервуар з водою; 5 – зливна трубка; 6 – кран для регулювання витрати води в трубопроводі; 7 – п’єзометрична трубка; 8 – трубка піто; 9 – кран.
Таблиця 3.1. Результати вимірів та розрахунків
Порядок обробки дослідних даних Розрахунки виконати послідовно для двох дослідів. 1. Визначити для кожного з п’яти перерізів величину п’єзометричного напору:
2. Визначити швидкісний напір 3. Визначити для кожного з п’яти перерізів величину повного напору:
4. Визначити втрату напору між початковим та кінцевим перерізами: h1-5=H1 – H5, см. Результати занести до таблиці 3.1. 5. За даними вимірів та обчислень побудувати діаграму рівняння Бернуллі для кожного з дослідів. Діаграму будують у наступній послідовності. На горизонтальній осі у масштабі відкладають відстань між перерізами та проставляють їх номери. Для кожного перерізу вверх у масштабі відкладають відрізки з відповідним значенням п’єзометричного напору 6. Зробити висновки. 3.6. Контрольні питання 1. Як записується рівняння Бернуллі для струминки ідеальної рідини?
2. Чим відрізняється рівняння Бернуллі для струминки реальної рідини від рівняння для струминки ідеальної рідини? 3. Як записується рівняння Бернуллі для потоку реальної рідини? 4. Від чого залежить коефіцієнт Коріоліса α? 5. Які члени рівняння Бернуллі відносяться до потенційної енергії, а які - до кінетичної? 6. Фізична та геометрична інтерпретація складових частин рівняння Бернуллі. 7. Що називається п’єзометричною лінією та лінією повного напору? 8. Наведіть приклади переходу потенційної енергії потоку в кінетичну і навпаки. 9. Яким чином за допомогою п’єзометра та трубки Піто можна визначити локальну швидкість потоку рідини у місці заміру? 10. Які умови застосування рівняння Бернуллі?
ЛАБОРАТОРНА РОБОТА № 4 ВИЗНАЧЕННЯ РЕЖИМІВ РУХУ РІДИНИ Мета роботи Дослідження режимів течії рідини за візуальними спостереженнями та з підрахунком числа Рейнольдса.
Теоретичні відомості При течії рідини режим її руху може бути ламінарнимабо турбулентним. При ламінарному режимі руху частинки рідини рухаються шарами, паралельно один одному без перемішування, рух має упорядкований характер.Струминки рідини мають різні швидкості, але швидкість кожної струминки є сталою та спрямованою вздовж потоку. При турбулентному русі частинки рідини рухаються з великими швидкостями в різних напрямках. Рух носить неупорядкований характер, при цьому частинки рухаються як в осьовому, так і радіальному напрямках. В кожній точці потоку відбуваються швидкі зміни швидкості в часі – так звані пульсації швидкості. Однак значення миттєвих швидкостей коливаються відносно деякої середньої швидкості. Два різних режими руху рідини та можливість взаємного переходу одного режиму до іншого можна спостерігати, пропускаючи по скляній трубі воду з різними швидкостями та вводячи по осі труби тонку струминку забарвленої рідини. При невеликих швидкостях забарвлена струминка рухається у воді прямолінійно, не перемішуючись із нею. Зі зростанням швидкості води забарвлена струминка починає набувати хвилястих обрисів, шлях її стає звивистим, але вона ще має чіткий обрис. При досягненні деякої критичної швидкості забарвлена струминка повністю руйнується, а вся маса води у скляній трубці підфарбовується, іншими словами, частинки рідини під час руху змішуються, і сам рух стає неупорядкованим. Різка зміна течії забарвленої струминки й характеризує перехід ламінарного режиму руху рідини до турбулентного.
Досліди, проведені О.Рейнольдсом, показали, що характер руху рідини залежить не тільки від середньої швидкості потоку рідини, але й від діаметра труби, густини та в’язкості рідини. Перехід одного виду руху до іншого відбувається при певному значенні комплексу перелічених величин, що називається критерієм Рейнольдса:
де u – середня швидкість потоку рідини, м/с; d – діаметр труби, м; ρ – густина рідини, кг/м3; μ - коефіцієнт динамічної в’язкості рідини, Па∙с. Критерій Рейнольдса є безрозмірною величиною. Із фізичної точки зору критерій Re є відношенням сил інерції до сил в’язкості. При русі рідини в трубах або каналах не круглого перерізу у вираз критерію Рейнольдса (4.1) замість діаметра підставляють величину еквівалентного діаметра:
де S – площа поперечного перерізу потоку, м2; П – змочений периметр, м. Із виразу (4.1) випливає, що турбулентний рух виникає зі збільшенням діаметра труби, швидкості руху та густини рідини або зі зменшенням в’язкості рідини. Величина числа Re, яка відповідає переходу одного виду руху в інший, називається критичним значенням числа Рейнольдса, так для прямих труб Reкр =2320. Рух рідини в прямих трубах при Re< 2320 є ламінарним. При Re> 2320 рух є турбулентним, проте розвинутого турбулентного характеру він набуває при Re> 10000. У межах Re від 2320 до 10000 турбулентний рух є недостатньо стійким (перехідна область). Розглянемо також розподіл швидкостей у перерізі труби при ламінарному та турбулентному русі рідини (рис. 4.1).
При ламінарному русі (рис. 4.1, а) швидкість частинок рідини у перерізу труби змінюється по параболі від нуля біля стінок труби до максимуму на її осі. При цьому середня швидкість рідини дорівнює половині максимальної υ cep = 0,5 υ max. Такий розподіл швидкостей встановлюється на деякій відстані від входу до труби. При турбулентному русі (рис. 4.1, б), внаслідок перемішування рідини, розподіл швидкостей в перерізі труби є більш рівномірним, ніж при ламінарному русі, при цьому υce p = (0,8…0,9) υmax. Але й при турбулентному русі в дуже тонкому граничному шарі біля стінок рух носить ламінарний характер. Цей шар товщиною δ називається ламінарним граничним шаром. Опис лабораторної установки Установка (рис. 4.2) складається з металевого бака 1 з водомірним склом 2. До бака приєднана скляна труба 3, на якій встановлено кран 4 для регулювання швидкості руху води. Це дозволяє створювати в трубці різні режими руху рідини. Зі скляної труби 3 вода надходить до мірної ємності 5. Над металевим баком розміщена посудина 6 із забарвленою рідиною, яка подається до труби 3 по її осі через капілярну трубку 7. Регулювання надходження забарвленої рідини здійснюється за допомогою затискача 8. Перед проведенням дослідів металевий бак 1 заповнюють водою через водопровідну трубу 9 з краном 10. Рівень води у баці під час дослідів підтримують сталим, регулюючи кран 10.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 441; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.192.3 (0.014 с.) |
 ,
см
(п’єзомет-рична висота)
,
см
(п’єзомет-рична висота)
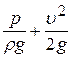 ,
см
,
см
 ,
см
,
см
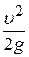 ,
см
(різниця між показанням трубки Піто та п’єзометра)
,
см
(різниця між показанням трубки Піто та п’єзометра)
 , см
, см
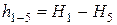 =, см
=, см
 в кожному перерізі як різницю відповідних показань трубки Піто та п’єзометра. При цьому слід зазначити, що визначений таким чином швидкісний напір відповідає локальному значенню швидкісного напору у місці заміру і дещо відрізняється від значення питомої кінетичної енергії для відповідного перерізу.
в кожному перерізі як різницю відповідних показань трубки Піто та п’єзометра. При цьому слід зазначити, що визначений таким чином швидкісний напір відповідає локальному значенню швидкісного напору у місці заміру і дещо відрізняється від значення питомої кінетичної енергії для відповідного перерізу. , см.
, см. . Верхні кінці відрізків з’єднують кривою, це і є п’єзометрична лінія. Приймаючи за початок відрахунку п’єзометричну лінію, будують лінію повного напору, для цього у кожному перерізі необхідно відкласти у вибраному масштабі вверх від п’єзометричної лінії відрізки, величини яких дорівнюють відповідному значенню
. Верхні кінці відрізків з’єднують кривою, це і є п’єзометрична лінія. Приймаючи за початок відрахунку п’єзометричну лінію, будують лінію повного напору, для цього у кожному перерізі необхідно відкласти у вибраному масштабі вверх від п’єзометричної лінії відрізки, величини яких дорівнюють відповідному значенню  , (4.1)
, (4.1)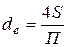 , (4.2)
, (4.2)




