
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Важнейшие формулы для расчета дк по первой группе предельных состояний. Расчет элементов дк по предельным состояниям второй группы.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Расчет элементов деревянных конструкций по предельным состояниям первой группы Центрально-растянутые и центрально-сжатые элементы Расчет центрально-растянутых элементов следует производить по формуле
где
Расчет центрально-сжатых элементов постоянного цельного сечения следует производить по формулам: а) на прочность
б) на устойчивость
Коэффициент продольного изгиба при гибкости элемента
коэффициент Гибкость элементов цельного сечения определяют по формуле: где
Расчетную длину элемента
Составные элементы на податливых соединениях, опертые всем сечением, следует рассчитывать на прочность и устойчивость по формулам (8) и (9), при этом
_______________ * Формула и экспликация к ней соответствуют оригиналу. - Примечание изготовителя базы данных.
Гибкость составного элемента, вычисленную по формуле (11), следует принимать не более гибкости
Гибкость составного элемента относительно оси, проходящей через центры тяжести сечений всех ветвей (ось Если ветви составного элемента имеют различное сечение, то расчетную гибкость
Составные элементы на податливых соединениях, часть ветвей которых не оперта по концам, допускается рассчитывать на прочность и устойчивость по формулам (5), (6) при соблюдении следующих условий: а) площади поперечного сечения элемента б) гибкость элемента относительно оси в) при определении гибкости относительно оси Расчет на устойчивость центрально-сжатых элементов переменного по высоте сечения следует выполнять по формуле:
|
||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 679; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.184.125 (0.01 с.) |

 (или
(или  ), (4)
), (4) - расчетная продольная сила;
- расчетная продольная сила; - расчетное сопротивление древесины растяжению вдоль волокон;
- расчетное сопротивление древесины растяжению вдоль волокон; - то же, для древесины из однонаправленного шпона (5.7);
- то же, для древесины из однонаправленного шпона (5.7); - площадь поперечного сечения элемента нетто.
- площадь поперечного сечения элемента нетто. (или
(или  ); (5)
); (5) (или
(или  - расчетное сопротивление древесины сжатию вдоль волокон;
- расчетное сопротивление древесины сжатию вдоль волокон;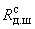 - то же, для древесины из однонаправленного шпона;
- то же, для древесины из однонаправленного шпона; - коэффициент продольного изгиба, определяемый согласно 6.3;
- коэффициент продольного изгиба, определяемый согласно 6.3;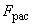 - расчетная площадь поперечного сечения элемента, принимаемая равной:
- расчетная площадь поперечного сечения элемента, принимаемая равной: 70
70 ; (7) при гибкости элемента
; (7) при гибкости элемента 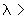 70
70 , (8) где коэффициент
, (8) где коэффициент  0,8 для древесины и
0,8 для древесины и  3000 для древесины и
3000 для древесины и  (9)
(9) - расчетная длина элемента;
- расчетная длина элемента;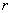 - радиус инерции сечения элемента с максимальными размерами брутто относительно осей
- радиус инерции сечения элемента с максимальными размерами брутто относительно осей 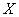 и
и  .
. на коэффициент
на коэффициент 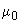
 (10)
(10)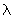 следует определять с учетом податливости соединений по формуле
следует определять с учетом податливости соединений по формуле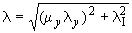 , (11)* где
, (11)* где  - гибкость всего элемента относительно оси
- гибкость всего элемента относительно оси  (рисунок 2), вычисленная по расчетной длине элемента
(рисунок 2), вычисленная по расчетной длине элемента  * - гибкость отдельной ветви относительно оси I-I (см. рисунок 2), вычисленная по расчетной длине ветви
* - гибкость отдельной ветви относительно оси I-I (см. рисунок 2), вычисленная по расчетной длине ветви 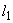 ; при
; при  ) ветви принимаются с
) ветви принимаются с  0*;
0*; - коэффициент приведения гибкости, определяемый по формуле
- коэффициент приведения гибкости, определяемый по формуле , (12), где
, (12), где  и
и  - ширина и высота поперечного сечения элемента, см;
- ширина и высота поперечного сечения элемента, см; - расчетное число швов в элементе, определяемое числом швов, по которым суммируется взаимный сдвиг элементов (на рисунке 2, а - 4 шва, на рисунке 2, б - 5 швов);
- расчетное число швов в элементе, определяемое числом швов, по которым суммируется взаимный сдвиг элементов (на рисунке 2, а - 4 шва, на рисунке 2, б - 5 швов); - расчетное число срезов связей в одном шве на 1 м элемента (при нескольких швах с различным числом срезов следует принимать среднее для всех швов число срезов);
- расчетное число срезов связей в одном шве на 1 м элемента (при нескольких швах с различным числом срезов следует принимать среднее для всех швов число срезов); - коэффициент податливости соединений, который следует определять по формулам таблицы 15.
- коэффициент податливости соединений, который следует определять по формулам таблицы 15.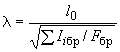 , (13), где
, (13), где  - сумма моментов инерции брутто поперечных сечений отдельных ветвей относительно собственных осей, параллельных ocи
- сумма моментов инерции брутто поперечных сечений отдельных ветвей относительно собственных осей, параллельных ocи  - площадь сечения брутто элемента;
- площадь сечения брутто элемента;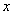 на рисунке 2), следует определять как для цельного элемента, т.е. без учета податливости связей, если ветви нагружены равномерно. В случае неравномерно нагруженных ветвей следует руководствоваться 6.7.
на рисунке 2), следует определять как для цельного элемента, т.е. без учета податливости связей, если ветви нагружены равномерно. В случае неравномерно нагруженных ветвей следует руководствоваться 6.7. , (14), определение
, (14), определение  приведено на рисунке 2.
приведено на рисунке 2. , (15), где
, (15), где  и
и 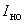 - моменты инерции поперечных сечений соответственно опертых и неопертых ветвей.
- моменты инерции поперечных сечений соответственно опертых и неопертых ветвей. (или
(или  - площадь поперечного сечения брутто с максимальными размерами;
- площадь поперечного сечения брутто с максимальными размерами; - коэффициент, учитывающий переменность высоты сечения, определяемый по таблице Е.1 приложения Е (для элементов постоянного сечения
- коэффициент, учитывающий переменность высоты сечения, определяемый по таблице Е.1 приложения Е (для элементов постоянного сечения 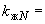 1);
1);


