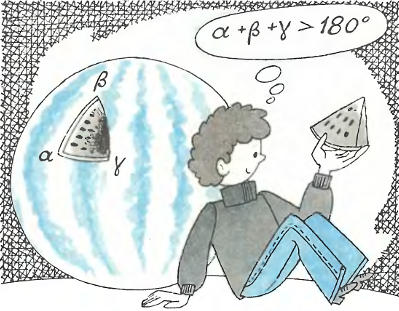Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Изогнутое пространство и искривленное времяСодержание книги
Поиск на нашем сайте
Казань середины прошлого века была грязным провинциальным городом, где редкие островерхие мечети контрастировали с луковицами православных церквей, а светлое, в несколько этажей, здание университета — с низкими, тесно прижавшимися друг к другу домишками вдоль пыльных улиц, по которым носились ватаги чумазых ребятишек. Трудно поверить, что в этих условиях могла родиться теория, перевернувшая представления, безраздельно владевшие умами более двух тысячелетий.
С тех пор как древнегреческий ученый Евклид собрал и привел в систему то, что стало потом называться евклидовой геометрией (она и сегодня излагается в школьных учебниках), считалось само собой разумеющимся, что окружающее нас пространство плоское, без всякой кривизны. Посмотрите на тонкий прут или лист бумаги. Это примеры одномерного и двумерного пространств. Они могут быть прямыми, плоскими и искривленными. Это понятно и не требует никаких пояснений. Сложнее представить искривление трехмерного пространства. Для этого нужно воображение или математические формулы. Например, сумма углов треугольника в искривленном пространстве не равна 180. Соответствующая теорема из школьного учебника там не пригодна, поскольку при ее выводе неявно предполагалось, что пространство может быть только плоским. На поверхности шара сумма углов треугольника больше 180°, на вогнутых поверхностях она меньше 180°. Читатель сам может найти другие величины, характеризующие кривизну пространства. С вершины современных знаний многое из того, что входило в науку с большим трудом, выглядит просто очевидным, и кажется невероятным, как это люди, а уж тем более знаменитые ученые, не могли понять таких простых вещей! Но именно такие простые, веками почитаемые за очевидные взгляды труднее всего изменить. Описывающая плоский мир геометрия Евклида более двух тысячелетий успешно служит людям, и никому в голову не приходило, что могут быть еще и другие геометрии, столь же последовательные и непротиворечивые, но только для искривленных миров. С точки зрения церковных догм, сама мысль о многообразии миров выглядела еретической и напоминала о трагической судьбе Джордано Бруно. Неудивительно, что когда ее высказал профессор математики Казанского университета Николай Иванович Лобачевский, его работы не нашли понимания даже у лучших математиков того времени. Он послал работы в Петербург, в Академию наук, но получил резкий отрицательный отзыв, подписанный знаменитым математиком Остроградским.
Правда, рассказывают, что здесь сыграло роль неудачное стечение обстоятельств. Остроградскому уже давно досаждал безграмотными математическими сочинениями некий чиновник Лобачевский. Получив новую работу, подписанную тем же именем да еще замахнувшуюся на тысячелетний авторитет Евклида, Остроградский пришел в крайнее раздражение и тут же написал разгромный отзыв. Как бы там ни было, отрицательное отношение Академии наук к работам казанского ученого подорвало его положение. Этим воспользовались чиновники и те из его коллег, которые раньше опасались открыто критиковать его взгляды (Лобачевский долгое время был ректором университета). К тому же резко ухудшилось зрение, и Лобачевский был вынужден уйти в отставку. Вскоре он умер, почти ослепший, неспособный заниматься своей любимой наукой. Лобачевский в своих книгах первым создал неевклидову геометрию и поставил вопрос: какова же реальная геометрия нашего мира — плоская евклидова или же искривленная неевклидова? Более того, он попытался ответить на этот вопрос экспериментально — путем астрономических наблюдений измерить сумму углов треугольника, образованного тремя яркими звездами. Работы Лобачевского и выполненные независимо от него расчеты венгерского математика Яноша Бояи, который тоже пришел к идее неевклидовых геометрий, послужили идейным фундаментом для всех последующих теорий искривленных пространств, в том числе и для теории Бернгарда Римана. Этот немецкий ученый разработал математический аппарат для анализа пространств различных типов. В его теории пространство могло быть скрученным и изогнутым, по-разному в различных точках, могло иметь разрывы и дырки, быть многомерным. Свои идеи Риман изложил в конкурсной лекции перед тем, как занять в Геттингенском университете место приват-доцента. В лекции, которая называлась «О гипотезах, лежащих в основаниях геометрии», не было ни одной формулы — для математического доклада факт весьма необычный. Рассказывают, что, выслушав Римана, престарелый «король математиков» Гаусс молча встал и вышел из зала. Лекция молодого ученого привела его «в состояние наивысшего изумления».
В начале XX века в распоряжении физиков были хорошо разработанные математические методы для описания искривленных пространств, а мысль о том, что при определенных условиях пространство может стать искривленным, уже не казалась еретической. Однако не было физической теории, которая бы связала кривизну пространства с действующими в нем силами. Такую теорию — теперь ее называют общей теорией относительности — создал Альберт Эйнштейн. В 1916 году он вместе с немецким математиком Гильбертом вывел уравнения, которые выразили кривизну пространства через силы всемирного тяготения. Оказалось, что там, где есть поле тяготения (гравитация), пространство всегда искривлено. И наоборот, пространственная кривизна проявляется в виде сил гравитации. Материальное тело как бы прогибает пространство и катится по образовавшейся ложбинке. Чем сильнее гравитация, тем такая ложбинка глубже.
И вот что замечательно: из уравнений Эйнштейна и Гильберта следует, что искривлено не только пространство, но и… время! Можно сказать, что темп его течения зависит от конкретных физических условий и разный в различных областях пространства. Этого не предвидели ни Лобачевский, ни Бояи. В перепадах гравитационных полей время может замедляться, почти замирать, или резко ускоряться. Однажды маленький сын спросил Эйнштейна, как он стал таким знаменитым, и тот ответил: — Когда слепой жук ползет по изогнутому суку, он не замечает, что сук изогнут. Мне посчастливилось заметить то, чего не заметил жук! Однако анализ новой теории, выполненный Фридманом, показал, что в ней содержится нечто большее: кривизна может стать такой большой, что пространство полностью замкнется и превратится в изолированный «пузырь».
|
||||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 77; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.238.67 (0.008 с.) |