Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение выпуклости вверх и вниз графика функции в интервале. ⇐ ПредыдущаяСтр 8 из 8
Кривая называется выпуклой вверх, если на этом интервале кривая лежит ниже любой своей касательной. Кривая называется выпуклой вниз, если на этом интервале кривая лежит выше любой своей касательной. Достаточный признак выпуклости вверх и вниз графика функции. Путь функция непрерывна на интервале (а, б) и имеет производные 1 и 2 порядка во всех точках этого интервала. Если во всех точках х, принадлежащих (а, б) f”(x) > 0, то на этом интервале y=f(x) выпукла вниз. Если во всех точках х, принадлежащих (а, б) f”(x) < 0, то на этом интервале y=f(x) выпукла вверх. Доказательство Предположим для определенности, что f ''(x) < 0 и докажем, что график функции будет выпуклым. Возьмем на графике функции y = f(x) произвольную точку M 0 с абсциссой x 0 Î (a; b) и проведем через точку M 0 касательную. Ее уравнение
Итак, уравнение кривой имеет вид y = f(x). Обозначим Разность f(x) – f(x 0) преобразуем по теореме Лагранжа Таким образом,
К выражению, стоящему в квадратных скобках снова применим теорему Лагранжа:
Таким образом, любая точка кривой лежит ниже касательной к кривой при всех значениях x и x 0 Î (a; b), а это значит, что кривая выпукла вверх. 25. Определение точки перегиба. Необходимый и достаточный признаки существования точки перегиба графика функции y= f(x) Определение. Рассмотрим функцию y=f(x), которая непрерывна и дифференцируема в точке х0.
Геометрический смысл точки перегиба состоит в том, что график функции f(x) переходит в этой точке с одной стороны касательной на другую.
x<x0 x>x0
Необходимый признак существования точки перегиба. Если x0 − точка перегиба функции f(x) и данная функция имеет вторую производную в некоторой окрестности точки х0, причем в точке x0 она непрерывна, то f ’’ (х0)=0. Доказательство. Дано: х0 – абсцисса точки перегиба функции y=f(x) Поскольку f’’(x) – непрерывна, то по свойству непрерывной функции она сохраняет знак в точке х0 и её окрестности. f ’’(х0)<0 ∀x∈(х0−δ,х0+δ) или f ’’(х0) >0 ∀x∈(х0−δ,х0+δ) В таком случае функция будет либо строго выпукла вверх (при f’’’(x)<0), либо строго выпукла вниз (при f ’’ (x)>0). Но тогда точка х0 не является точкой перегиба, что противоречит условию. Следовательно, предположение неверно и вторая производная в точке перегиба должна быть равна нулю.
Согласно необходимому условию существования точки перегиба, эти точки находятся среди точек, в которых f ’’(x) равна нулю либо не существует. Точки, в которых f ”(x) равна нулю либо не существует, называются критическими для перегиба (или подозрительными на перегиб), однако не во всякой критической точке будет точка перегиба. Первое достаточное условие существования точки перегиба Если функция f(x) непрерывна и дифференцируема в точке x0, имеет вторую производную f′′(x0) в некоторой проколотой δ-окрестности точки x0 и если вторая производная меняет знак при переходе через точку x0, то x0 является точкой перегиба функции f(x). Доказательство.
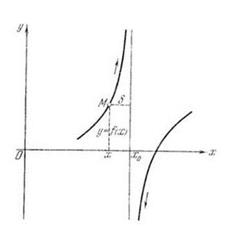
В таком случае, согласно достаточным условиям выпуклости, функция f(x) выпукла вниз в левой δ-окрестности точки x0 и выпукла вверх в правой δ-окрестности. Следовательно, в точке x0 функция меняет направление выпуклости, т.е. c является, по определению, точкой перегиба. Второе достаточное условие существования точки перегиба 26 Асимптоты графика функции y = f (x). Нахождение вертикальных и наклонных асимптот. Теорема о существовании наклонной асимптоты графика функции (доказательство). Асимптоты графика функции Пусть точка М(x;y) перемещается по графику функции y=f(x), неограниченно удаляясь от начала координат. Если при этом расстояние от т.М до некоторой прямой стремится к 0, то такая прямая- асимптота графика функции y=f(x) . Определение. Прямая L называется асимптотой кривой Г, если расстояние от точки М кривой Г до прямой L стремится к нулю, когда точка М, двигаясь по кривой, бесконечно удаляется от начала координат. Различают два вида асимптот: наклонные и вертикальные. Горизонтальные- частный случай НА. Вертикальная асимптота Вертикальная асимптота- вертикальная прямая, уравнение которой Если функция Верно обратное утверждение: если Вывод: для нахождения вертикальной асимптоты бесконечного разрыва этой функции. Наклонная асимптота НА имеет вид y=kx+b Для того, чтобы график функции y=f(x) имел наклонную асимптоту L: y=kx+b, необходимо и достаточно, чтобы Необходимость Дано: L: y=kx+b – НА графика функции. Доказать: Док-во:
MР перп. L МN перп. 0X MP=
Распишем MN:
MР перп. L МN перп. 0X MP=
Распишем MN:
Достаточность Дано: L: y=kx+b – НА графика функции Доказать:: L: y=kx+b – НА графика функции Док-во: Найдем разность ординат графика функции y=f(x) и прямой L: y=kx+b
Вывод y=kx+b, где Замечание График функции может пересекать наклонную асимптоту, но вертикальную не пересекает.
|
||||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 723; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.154.208 (0.03 с.) |
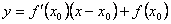 . Мы должны показать, что график функции на (a; b) лежит ниже этой касательной, т.е. при одном и том же значении x ордината кривой y = f(x) будет меньше ордината касательной.
. Мы должны показать, что график функции на (a; b) лежит ниже этой касательной, т.е. при одном и том же значении x ордината кривой y = f(x) будет меньше ордината касательной.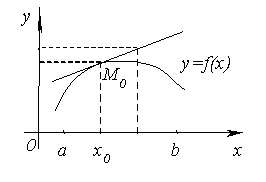
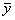 ординату касательной, соответствующую абсциссе x. Тогда
ординату касательной, соответствующую абсциссе x. Тогда 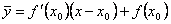 . Следовательно, разность ординат кривой и касательной при одном и том же значении x будет
. Следовательно, разность ординат кривой и касательной при одном и том же значении x будет 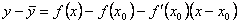 .
.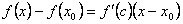 , где c между x и x 0.
, где c между x и x 0.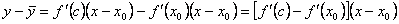 .
.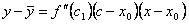 , где c 1 между c 0 и x 0. По условию теоремы f ''(x) < 0. Определим знак произведения второго и третьего сомножителей.
, где c 1 между c 0 и x 0. По условию теоремы f ''(x) < 0. Определим знак произведения второго и третьего сомножителей. (x – x 0) > 0 и (c – x 0) > 0. Поэтому
(x – x 0) > 0 и (c – x 0) > 0. Поэтому 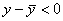 .
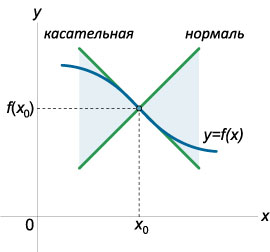
.
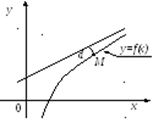
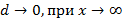
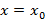 .
. 
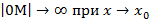
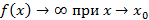 ,или хотя бы один из односторонних пределов бесконечен
,или хотя бы один из односторонних пределов бесконечен 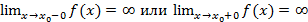 , то
, то 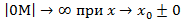 , следовательно по определению ВА
, следовательно по определению ВА 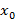
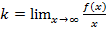 ,
, 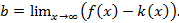
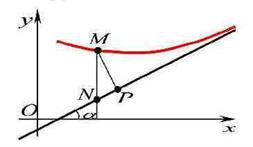
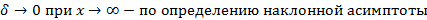
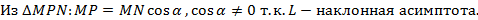
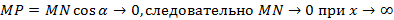
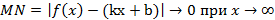
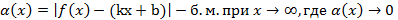
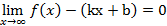
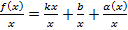 ,
, 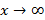
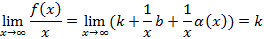
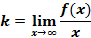
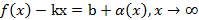
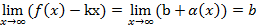
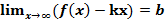
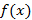 .
. 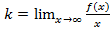 ,
, 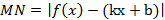
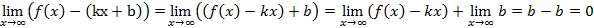
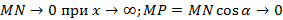 (по определению НА): L: y=kx+b – НА графика функции
(по определению НА): L: y=kx+b – НА графика функции