
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теоремы о пределах: предел суммы, произведения и частного двух функций, имеющих предел (с доказательством одной из теорем)
1) Предел суммы двух функций равен сумме их пределов: Доказательство: Пусть Тогда по теореме о связи функции, её предела и бесконечно малой функции:
По теореме о связи функции, её предела и бесконечно малой функции
2) Предел произведения двух функций равен произведению их пределов: Доказательство: Пусть
Выражения в скобках, по свойствам бесконечно малых функций, - бесконечно малая функция. Тогда 3) Предел частного двух функций равен пределу делимого, деленного на предел делителя, если предел делителя не равен:
Доказательство: Пусть
По свойствам бесконечно малых функций, второе слагаемое – бесконечно малая функция. Поэтому Сравнение бесконечно малых. Символ,,о”- малое. Теоремы об эквивалентных бесконечно малых величинах (с доказательством одной из них). Вышмат. Вопрос 6. Сравнение бесконечно малых. Символ,,о”- малое. Теоремы об эквивалентных бесконечно малых величинах (с доказательством одной из них).
Определение: Пусть · Если предел отношения Обозначение: α =о(β) или α << β Читается: a есть «o - малое от b» · Если существует конечный, отличный от нуля, предел их отношений, то бесконечно малые величины a и b называются б.м. одного порядка малости a · Нет необходимости рассматривать случай, когда предел отношения так как в этом случае предел отношения б/а (бета к альфа) равен нулю, значит b является б.м. более высокого порядка, чем a.
· Если же не существует ни конечного, ни бесконечного предела отношения бесконечно малых a и b, то говорят, что эти бесконечно малые не сравнимые по отношению. · Если предел отношения Эквивалентными бесконечно малыми называются 2 бесконечно малые а и б (альфа и бета) одновременно стремящиеся к 0, предел отношения которых равен 1
Свойства эквивалентных бесконечно малых (теоремы) нулю, были эквивалентны, необходимо и достаточно, чтобы их разность была бесконечно малой более высокого порядка малости, чем любая из них. Доказательство. Доказательство (только для удобства записи) проведем для случая, когда
Необходимость. Дано что Надо доказать. что
Найдем Это значит, что
Достаточность. Дано, что Надо доказать, что
▲Так как
отсюда
2) Предел отношений двух бесконечно малых не изменится, если любую из них заменить на ей эквивалентную. Доказательство. ▲Пусть Дано, что при
|
|||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 2026; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.200.211 (0.009 с.) |
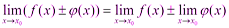
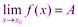 ,
, 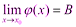
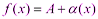

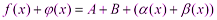 , где
, где 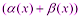 - бесконечно малая функция (по свойству бесконечно малых функций).
- бесконечно малая функция (по свойству бесконечно малых функций).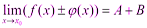 или
или 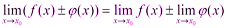

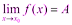 ,
, 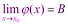 Тогда
Тогда 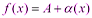 ,
, 
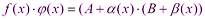

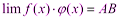 , т.е.
, т.е. 
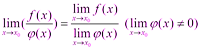
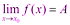 ,
,  Тогда
Тогда 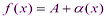 и
и 
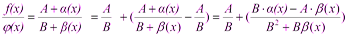
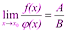 , т.е.
, т.е. 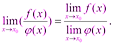
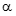 и
и  бесконечно малые величины, одновременно стремящихся к нулю.
бесконечно малые величины, одновременно стремящихся к нулю. равен нулю, то бесконечно малая величина
равен нулю, то бесконечно малая величина 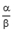 равен бесконечности,
равен бесконечности,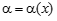 и
и  - функции, являющиеся бесконечно малыми при
- функции, являющиеся бесконечно малыми при 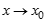 .
. (альфа экв. Бета) при
(альфа экв. Бета) при  (или
(или 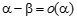 ) при
) при  ▲Обозначим
▲Обозначим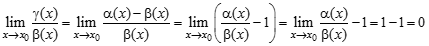 .
.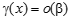 или
или 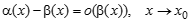 . ▲
. ▲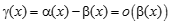 при
при 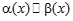 (альфа экв. Бета) при
(альфа экв. Бета) при  , то
, то 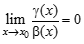 ;
;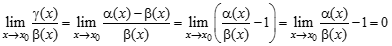 ,
,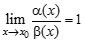 , т. е.
, т. е.  и
и 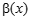 - бесконечно малые функции при
- бесконечно малые функции при 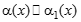 ,
, 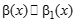 (альфа экв. Альфа 1, бета экв. Бета 1).
(альфа экв. Альфа 1, бета экв. Бета 1).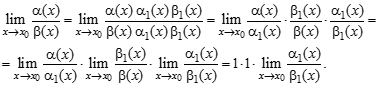
 ▲
▲


