
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Следствия 2-го замечательного предела:
1) Обозначим
2) Так как при x→0 имеем 3) 4)
1)
Сделаем замену переменной Получаем Таким образом Совершенно аналогично можно показать, что
2)
Здесь, забегая немного вперед, воспользуемся тем, что знаки предела и логарифма можно поменять местами в силу того, что функция Тогда Доказано, что Совершенно аналогично можно показать (воспользовавшись правилом перехода к логарифму с другим основанием), что 9. Понятие о приращении функции y = f (x). Определение функции y = f (x), непрерывной в точке. Непрерывность суммы, произведения и частного двух непрерывных функций (с доказательством одной из теорем). Два определения непрерывности функции в точке, их равносильность. Точки разрыва и их классификация. Приращением переменной величины называется разность между 2-умя её значениями. ∆X=X-X0 Пусть переменной величиной является функция: Опр. Приращением ∆у функции у=f(x) является разность между 2-умя различными значениями функции, т.е. разность между значениями функции в 2-ух разных точках (Х и Х0)
Опр 1: Функция y=f(x) непрерывной в точке x0, если выполнены 3 условия: А) Функция определена в т. Х0 и некоторой её окрестности. Б) Существует предел функции f(x) в т. X0, т.е. ᴟlim f(x),при X→X0 В) Этот предел равен значению функции в точке X0, т.е. lim f(x)=f(x0), при X→X0 lim f(x)=А,при X→X0, А=f(X0) lim f(x)=f(x0)=Ɐɛ>0 ᴟδ(ɛ)>0: ⱯX:|X-X0|<δ ==→|f(X)-f(X0)|<ɛ Опр 2: Функция у=f(x) называется непрерывной в т.X0, если она определена в т. X0 и некоторой её окрестности и бесконечно малому приращению аргумента ∆x соответствует бесконечно малое приращение функции в т. Х0, т.е: lim ∆y(X0)=0, при ∆X→0 Два определения непрерывности функции в точке, их равносильность. lim f(x)=f(x0), при X→X0 ----→(по теореме о разности функции и её пределом – Н.У.) f(x)=f(x0)+α(x), α(x)-б.м.(при Х→Х0 или при ∆Х→0). α(х)=f(X)-f(X0)=∆y(X0). lim α(x), при ∆x→0 = lim ∆y(X0)=0, при ∆x→0.
Теорема о непрерывности результата арифметических действий с непрерывными функциями: Если функция f(x) и Ф(х) непрерывны в т Х0, то их сумма f(x)+Ф(х), разность, произведение и частное(Ф(Х0)≠0) также непрерывны в т Х0. Док-во произведения: Пусть f(x), Ф(х) – непрерывны в т Х0. Рассмотрим у(х)=f(x)*Ф(х). lim y(x), при X→X0 = lim f(x)*Ф(х), при Х→Х0 =(по св-ву пределов) lim f(x), при Х→Х0*lim Ф(х), при Х→Х0=[по условию теоремы) f(x) непрерывна в т X0, lim f(Х)=f(X0), при Х→Х0 Ф(х) непрерывна в т Х0, lim Ф(Х)=Ф(Х0), при Х→Х0] =f(Х0)*Ф(Х0), т.е. lim f(X0)*Ф(X0), при Х→Х0=f(X0)*Ф(Х0)---→ по опр непрерывности 1 f(x)*Ф(х) непрерывно в т Х0
Опр. Т. Х=Х0 – точка разрыва функции у=f(x), если нарушено хотя бы одно из условий непрерывности функции в т Х=Х0(см опр1). Различают устраненный разрыв, разрыв 1-ого рода (со скачком) и разрыв 2-ого рода. Устраненный разрыв: т.Х=Х0 – есть точка устраненного разрыва, если односторонние пределы функции у-f(x) в т X0 существуют, равны и предел функции в т. Х0 не равен значению функции в т. Х0 Возникает, если функция «плохо» определена или не определена. Разрыв 1-ого рода(со скачком) возникает, если односторонние пределы существуют, но не равны. Разрыв 2-ого рода возникает, если хотя бы 1 из односторонних пределов не существует или бесконечен.
|
|||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 169; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.206.73 (0.009 с.) |
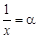 , тогда
, тогда 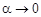 при
при  и второй замечательный предел примет вид
и второй замечательный предел примет вид .
.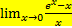 =e
=e −1→0, то в рассматриваемом пределе наличествует неопределённость вида
−1→0, то в рассматриваемом пределе наличествует неопределённость вида  .Для раскрытия этой неопределённости осуществим замену переменной, обозначив t=ex−1. Так как x→0, то t→0. Далее, из формулы t=
.Для раскрытия этой неопределённости осуществим замену переменной, обозначив t=ex−1. Так как x→0, то t→0. Далее, из формулы t= 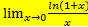 =1
=1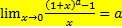

 ;
;  при
при 
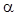 и
и 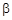 являются б. м.:
являются б. м.: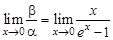 .
. ,
,  при
при 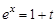 ;
;  и
и .
.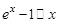 при
при 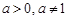
 при
при 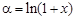 и
и 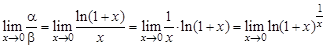 .
.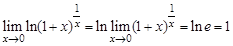 .
.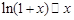 при
при 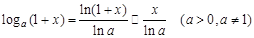 .
. ∆Y(X0)=Y-Y0=f(X)-f(X0)=f(X0+∆X)-f(X0)
∆Y(X0)=Y-Y0=f(X)-f(X0)=f(X0+∆X)-f(X0)


