Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема Ролля, доказательство, геометрическая интерпретация.
Теорема Ролля Теорема. Пусть функция y=f(x) непрерывна на отрезке [a,b], имеет производную f’(x) на интервале (a,b) и при этом f(a)=f(b). Тогда существует точка c ∈ (a,b), в которой выполнено условие f’(c)=0. Доказательство. Функция y=f(x) непрерывна на отрезке [a,b] и, следовательно, достигает на этом отрезке свое наибольшее и наименьшее значение. Если эти значения совпадают, то функция равна константе, и ее производная равна 0 в каждой точке интервала (a,b). Если же наибольшее и наименьшее значения функции не совпадают, то хотя бы одно из них не совпадает со значением функции на границах отрезка. Пусть в точке c ∈ (a,b) достигается наибольшее или наименьшее значение функции на отрезке. Тогда эта точка является точкой экстремума и в этой точке по теореме Ферма производная равна 0. Геометрическая интерпретация. Теорема означает, что если функция y=f(x) удовлетворяет теореме Ролля, то найдется хотя бы одна точка С такая, что касательная к графику функции, проведенная в этой точке, параллельная оси Ox.
Следствие. Если f(a)=f(b)=0, то теорему Ролля можно сформулировать следующим образом: между двумя последовательными нулями непрерывной дифференцируемой функции имеется, хотя бы один, нуль производной. 20. Теорема Коши. Теорема Лагранжа, доказательство, геометрический смысл. Теорема Лагранжа: Если функция Геометрический смысл теоремы Лагранжа: Если в каждой точке дуги кривой существует касательная, то на дуге графика функции
Дано: Доказать: Доказательство: Введем вспомогательную функцию
1. 2. 3.
По теореме Ролля:
Теорема Коши. Теорема Коши (об отношении приращений двух функций). Если функции y = f (x) и y = g(x) 1) непрерывны на отрезке [a;b]; 2) дифференцируемы на интервале (a;b); 3) производная g′(x) ≠ 0 на интервале (a;b). Тогда на интервале (a;b) найдется по крайней мере одна точка x0 такая, что
Из условия теоремы следует, что g′(x) ≠ 0. Это означает, что разность g (b) − g (a) ≠ 0. Действительно, если бы g (b) − g (a) = 0, то функция y = g (x), являясь непрерывной и дифференцируемой, удовлетворяла бы условиям теоремы Ролля и в таком случае g ′(x) была бы равна нулю по крайней мере в одной точке x0 интервала (a; b), что противоречит условию. Введем вспомогательную функцию
Эта функция удовлетворяет всем условиям теоремы Ролля: 1) F(x) непрерывна на отрезке [a;b], так как непрерывны функции у = f (x) и y = g (x); 2) функция F(x) имеет производную всюду в интервале (a;b), поскольку каждое слагаемое в правой части функции F(x) имеет производную на этом интервале; 3) F (a) = F (b) = 0, в чем убеждаемся непосредственной проверкой. Из теоремы Ролля делаем вывод о существовании точки x0, что F ′(x0) = 0. Поэтому Отсюда следует Теорема Лагранжа является частным случаем теоремы Коши: достаточно в теореме Коши взять g(x)=x. Геометрический смысл теоремы Коши Пусть плоская кривая γ описывается параметрическими уравнениями
21. Определение дифференцируемой функции 1. Определение: Функция Другая формулировка:
Приращение дифференцируемой функции имеет 2 слагаемых 1) 2) 2. Определение: Дифференциал независимой переменной
3. Геометрический смысл дифференциала в точке: Искомая прямая Прямая
22. Определение функции y = f (x), возрастающей (убывающей) в интервале. Доказательство достаточного признака возрастания (убывания) функции на интервале.
|
||||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 1547; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.122.162 (0.013 с.) |
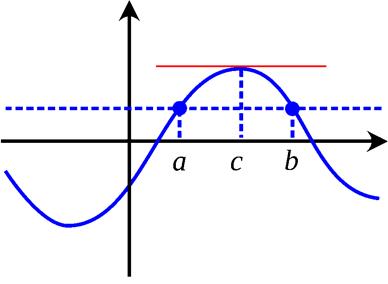
 непрерывна на отрезке
непрерывна на отрезке 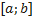 , дифференцируема на
, дифференцируема на  , то найдется хотя бы одна точка
, то найдется хотя бы одна точка  такая, что
такая, что 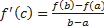 .
.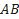 , стягивающей эту дугу.
, стягивающей эту дугу.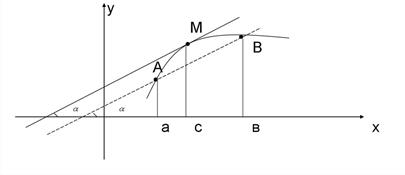
 – непрерывна на
– непрерывна на 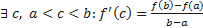
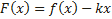 , где
, где 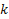 – угловой коэффициент
– угловой коэффициент  ,
,  ,
, 
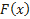 – удовлетворяет условиям теоремы Ролля:
– удовлетворяет условиям теоремы Ролля: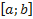 ;
;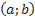 ;
;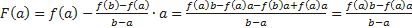

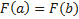
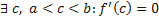 ,
,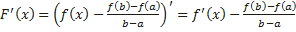
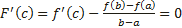
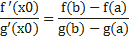
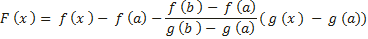

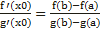
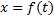 ,
, 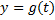 , где параметр
, где параметр  изменяется в промежутке
изменяется в промежутке  . При изменении параметра
. При изменении параметра  до
до  . В соответствии с теоремой Коши на кривой
. В соответствии с теоремой Коши на кривой  найдется точка
найдется точка 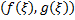 , в которой касательная параллельна хорде, соединяющей концы
, в которой касательная параллельна хорде, соединяющей концы  и
и 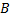 данной кривой.
данной кривой.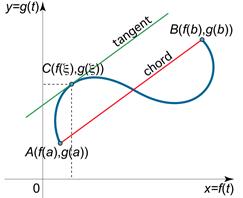
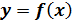 в точке
в точке  . Определение дифференциала
. Определение дифференциала 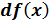 . Геометрический смысл дифференциала
. Геометрический смысл дифференциала 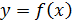 называется дифференцированной в точке
называется дифференцированной в точке 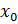 , если ее приращение в этой точке может быть представлено в виде
, если ее приращение в этой точке может быть представлено в виде 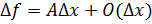 , где
, где 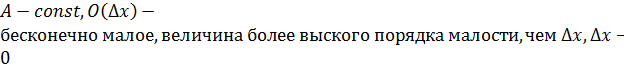
 называется дифференцированной в точке, если приращение в этой точке допускает выделение главной части линейной приращения аргумента
называется дифференцированной в точке, если приращение в этой точке допускает выделение главной части линейной приращения аргумента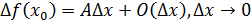
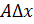 – главная по значению линейная относительно
– главная по значению линейная относительно  часть приращения функции
часть приращения функции 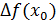 , называется главная часть
, называется главная часть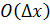 – бесконечно малое более высокого порядка малости, чем
– бесконечно малое более высокого порядка малости, чем 
 равен приращения независимой переменной
равен приращения независимой переменной 
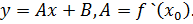
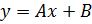 имеет угловой коэффициент
имеет угловой коэффициент  и проходит через точку
и проходит через точку 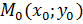 ,
, 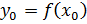 , данная прямая – касательная к графику функции в точке
, данная прямая – касательная к графику функции в точке 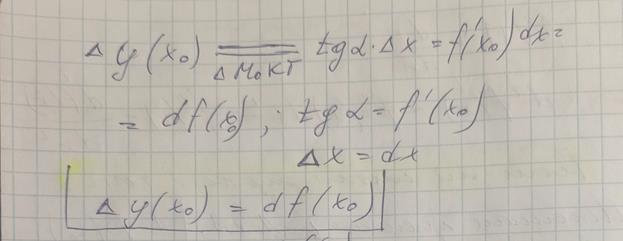
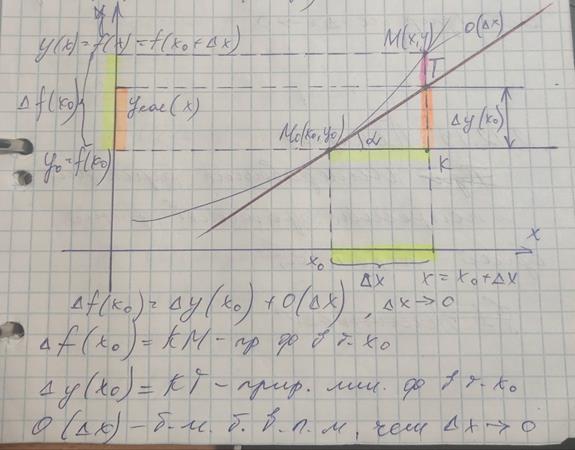 Дифференциал функции в точке
Дифференциал функции в точке