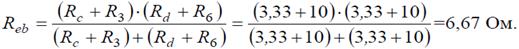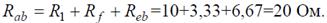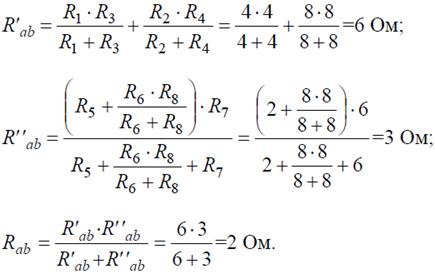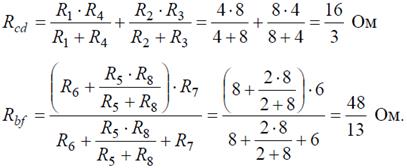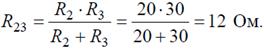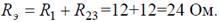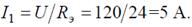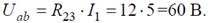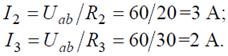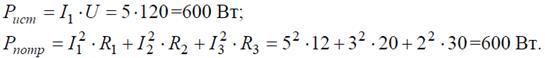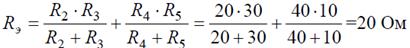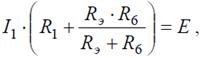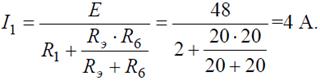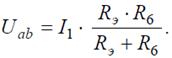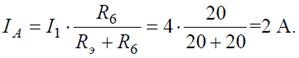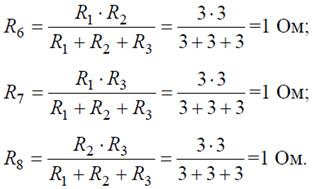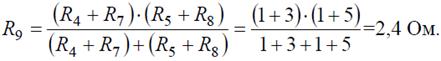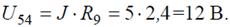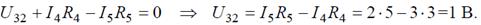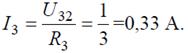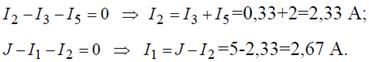Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Применение законов Ома и Кирхгофа для расчета электрической цепиСодержание книги
Поиск на нашем сайте
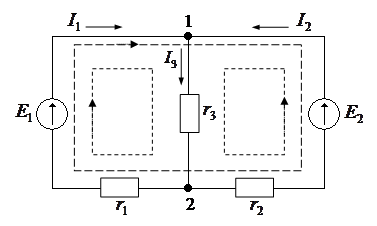
При помощи закона Ома и двух законов Кирхгофа можно рассчитать режим работы электрической цепи любой сложности. Общей задачей расчета является определение токов во всех участках цепи при заданных параметрах элементов цепи и известной конфигурации цепи. Для составления уравнений по закону Ома и двум законам Кирхгофа следует, прежде всего, выбрать направления токов во всех ветвях рассчитываемой цепи.
При записи уравнений для узлов цепи по первому закону Кирхгофа необходимо иметь в виду, что число независимых уравнений на единицу меньше общего числа узлов y, то есть нужно составить y – 1 уравнение. Действительно, если составить уравнения для всех y узлов, то ток каждой ветви войдет дважды в уравнение, так как ветвь соединяет два узла с противоположными знаками. При суммировании всех левых частей уравнений, составленных по первому закону Кирхгофа, получается тождественно ноль. При составлении уравнений на основании второго закона Кирхгофа необходимо также составить независимую систему. В частности, независимая система будет получена, если выбрать контуры так, чтобы каждый следующий содержал хотя бы одну ветвь, не вошедшую в контуры, для которых уже составлены уравнения. Такие контуры называются независимыми. Число неизвестных токов равно числу ветвей b. Для определения этих токов необходимо составить b независимых уравнений. Так как по первому закону Кирхгофа составляется y – 1 независимых уравнений, то на основании второго закона Кирхгофа должно быть составлено b – (y – 1) уравнений. Например, для нашей цепи может быть составлено два уравнения по первому закону Кирхгофа (для узлов 1, 2):
На основании второго закона Кирхгофа и закона Ома можно составить три уравнения для трех контуров. Для контура 1:
для контура 2:
для контура 3:
Для приведенной схемы число узлов y = 2, то есть по первому закону Кирхгофа нужно составить одно уравнение (2–1=1). Число неизвестных токов равно числу ветвей b = 3. Следовательно, по второму закону Кирхгофа должно быть составлено два уравнения (3–(2–1)=2). Из трех контуров этой цепи в качестве независимых можно взять любую пару контуров. После совместного решения системы независимых уравнений определяются токи в ветвях цепи. Если для какого-либо тока будет получено отрицательное значение, то из этого следует, что его действительное направление противоположно выбранному. Применение этого метода для сложных цепей часто требует значительной затраты времени, поэтому желательно, когда это возможно, вести расчеты более простыми методами.
Решение задач Расчет электрических цепей постоянного тока методом эквивалентных преобразований Задача 1. Для цепи (рис. 1), определить эквивалентное сопротивление относительно входных зажимов a−g, если известно: R 1 = R 2 = 0,5 Ом, R 3 = 8 Ом, R 4 = R 5 = 1 Ом, R 6 = 12 Ом, R 7 = 15 Ом, R 8 = 2 Ом, R 9 = 10 Ом, R 10= 20 Ом.
Рис. 1 Решение Начнем эквивалентные преобразования схемы с ветви наиболее удаленной от источника, т.е. от зажимов a−g:
Задача 2. Для цепи (рис. 2, а), определить входное сопротивление если известно: R 1 = R 2 = R 3 = R 4= 40 Ом.
Решение Исходную схему можно перечертить относительно входных зажимов (рис. 2, б), из чего видно, что все сопротивления включены параллельно. Так как величины сопротивлений равны, то для определения величины эквивалентного сопротивления можно воспользоваться формулой:
n – количество параллельно соединенных сопротивлений.
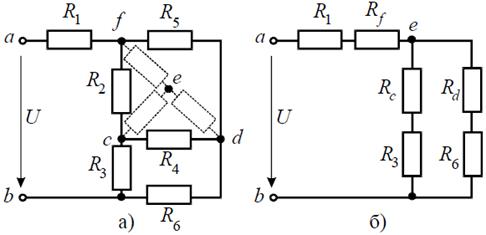
Задача 3. Определить эквивалентное сопротивление относительно зажимов a–b, если R 1 = R 2 = R 3 = R 4 = R 5 = R 6 = 10 Ом (рис. 3, а).
Рис. 3 Решение Преобразуем соединение «треугольник» f−d−c в эквивалентную «звезду». Определяем величины преобразованных сопротивлений (рис. 3, б):
И тогда эквивалентное сопротивление исходной схемы представляет последовательное соединение сопротивлений:
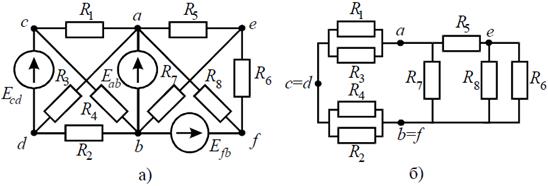
Задача 4. В заданной цепи (рис. 4, а) определить методом эквивалентных преобразований входные сопротивления ветвей a−b, c–d и f−b, если известно, что: R 1 = 4 Ом, R 2 = 8 Ом, R 3 =4 Ом, R 4 = 8 Ом, R 5 = 2 Ом, R 6 = 8 Ом, R 7 = 6 Ом, R 8 =8 Ом. Решение Для определения входного сопротивления ветвей исключают из схемы все источники ЭДС. При этом точки c и d, а также b и f соединяются накоротко, т.к. внутренние сопротивления идеальных источников напряжения равны нулю.
Рис. 4 Ветвь a−b разрывают, и т.к. сопротивление Ra–b = 0, то входное сопротивление ветви равно эквивалентному сопротивлению схемы относительно точек a и b (рис. 4, б):
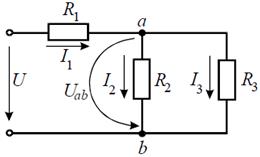
Аналогично методом эквивалентных преобразований определяются входные сопротивления ветвей Rcd и Rbf. Причем, при вычислении сопротивлений учтено, что соединение накоротко точек a и b исключает («закорачивает») из схемы сопротивления R 1, R 2, R 3, R 4 в первом случае, и R 5, R 6, R 7, R 8 во втором случае.
Задача 5. В цепи (рис. 5) определить методом эквивалентных преобразований токи I 1, I 2, I 3и составить баланс мощностей, если известно: R 1 = 12 Ом, R 2 = 20 Ом, R 3 = 30 Ом, U = 120 В.
Рис. 5 Решение Эквивалентное сопротивление для параллельно включенных сопротивлений:
Эквивалентное сопротивление всей цепи:
Ток в неразветвленной части схемы:
Напряжение на параллельных сопротивлениях:
Токи в параллельных ветвях:
Баланс мощностей:
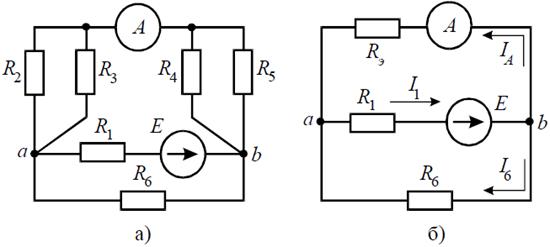
Задача 6. В цепи (рис. 6, а), определить методом эквивалентных преобразований показания амперметра, если известно: R 1 = 2 Ом, R 2 = 20 Ом, R 3 = 30 Ом, R 4 = 40 Ом, R 5 = 10 Ом, R 6 = 20 Ом, E = 48 В. Сопротивление амперметра можно считать равным нулю.
Рис. 6 Решение Если сопротивления R 2, R 3, R 4, R 5 заменить одним эквивалентным сопротивлением RЭ, то исходную схему можно представить в упрощенном виде (рис. 6, б). Величина эквивалентного сопротивления:
Преобразовав параллельное соединение сопротивлений RЭ и R 6 схемы (рис. 6, б), получим замкнутый контур, для которого по второму закону Кирхгофа можно записать уравнение:
откуда ток I 1:
Напряжение на зажимах параллельных ветвей Uab выразим из уравнения по закону Ома для пассивной ветви, полученной преобразованием RЭ и R 6:
Тогда амперметр покажет ток:
Задача 7. Определить токи ветвей схемы методом эквивалентных преобразований (рис. 7, а), если R 1 = R 2 = R 3 = R 4 = 3 Ом, J = 5 А, R 5 = 5 Ом.
Рис. 7 Решение Преобразуем «треугольник» сопротивлений R 1, R 2, R 3 в эквивалентную «звезду» R 6, R 7, R 8 (рис. 7, б) и определим величины полученных сопротивлений:
Преобразуем параллельное соединение ветвей между узлами 4 и 5
Ток в контуре, полученном в результате преобразований, считаем равным току источника тока J, и тогда напряжение:
И теперь можно определить токи I 4 и I 5:
Возвращаясь к исходной схеме, определим напряжение U 32 из уравнения по второму закону Кирхгофа:
Тогда ток в ветви с сопротивлением R 3 определится:
Величины оставшихся неизвестными токов можно определить из уравнений по первому закону Кирхгофа для узлов 3 и 1:
|
||||
|
Последнее изменение этой страницы: 2021-06-14; просмотров: 209; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.12.61 (0.007 с.) |

 .
.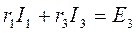 ,
,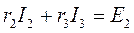 ,
,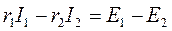 .
.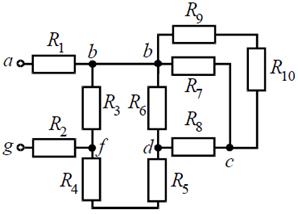
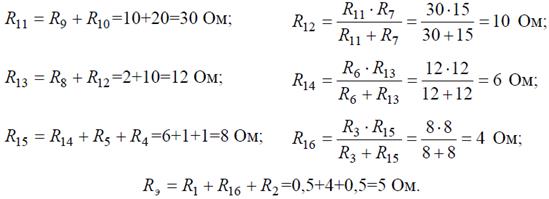
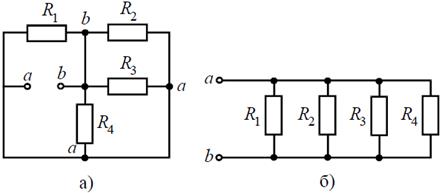 Рис. 2
Рис. 2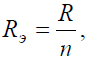 где R – величина сопротивления, Ом;
где R – величина сопротивления, Ом;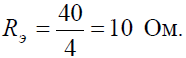
 По условию задачи величины всех сопротивлений равны, а значит:
По условию задачи величины всех сопротивлений равны, а значит: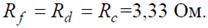 На преобразованной схеме получили параллельное соединение ветвей между узлами e–b, тогда эквивалентное сопротивление равно:
На преобразованной схеме получили параллельное соединение ветвей между узлами e–b, тогда эквивалентное сопротивление равно: