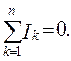Линейные электрические цепи постоянного тока

Электрической цепью называют совокупность источников питания (генераторы, гальванические элементы, аккумуляторные батареи и др.) и приемников электрической энергии (электрические двигатели, источники света, нагревательные элементы и др.) и соединяющих их проводов, создающих путь для электрического тока, процессы в которой описывают с помощью понятий электродвижущей силы (ЭДС), тока, напряжения.

Источники питания, приемники электрической энергии, соединяющие их провода являются основными элементами электрической цепи. К элементам цепи относятся также аппараты управления (автоматы, контакторы, магнитные пускатели и др.), защиты (предохранители, тепловые реле и др.), преобразующие устройства (трансформаторы, выпрямители и др.) и электроизмерительные приборы.

Графическое изображение элементов электрической цепи с помощью условных обозначений (согласно действующему ГОСТу) называется электрической схемой. Ниже приведены некоторые условные обозначения элементов электрической цепи

- гальванический  и аккумуляторный элементы

    источник ЭДС

                                                                                                                          источник тока

  генератор постоянного тока

двигатель постоянного тока

 

  лампа накаливания

 

 

- нагревательный элемент

 

- резистор

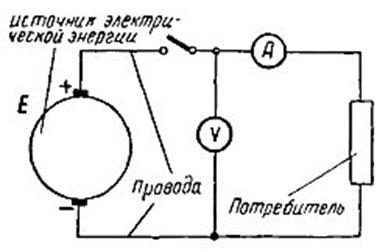
Простейшая электрическая установка состоит из источника (гальванического элемента, аккумулятора, генератора и т. п.), потребителей или приемников электрической энергии (ламп накаливания, электронагревательных приборов, электродвигателей и т. п.) и соединительных проводов, соединяющих зажимы источника напряжения с зажимами потребителя. Т.е. электрическая цепь - совокупность соединенных между собой источников электрической энергии, приемников и соединяющих их проводов (линия передачи).

Основные элементы цепи.

Все электроприемники характеризуются электрическими параметрами, среди которых основные - напряжение и мощность. Для нормальной работы электроприемника на его зажимах необходимо поддерживать номинальное напряжение.

Элементы электрической цепи делятся на активные и пассивные.

К активным элементам электрической цепи относятся те, в которых индуцируется ЭДС (источники ЭДС, электродвигатели, аккумуляторы в процессе зарядки и т. п.).

 К пассивным элементам относятся электроприемники и соединительные провода.

Элементы электрической цепи, обладающие электрическим сопротивлением и называемые резисторами, характеризуются так называемой вольт-амперной характеристикой - зависимостью напряжения на зажимах элемента от тока в нем или зависимостью тока в элементе от напряжения на его зажимах.

Если сопротивление элемента постоянно при любом значении тока в нем и любом значении приложенного к нему напряжения, то вольт-амперная характеристика прямая линия и такой элемент называется линейным элементом.

В общем случае сопротивление зависит как от тока, так и от напряжения. Одна из причин этого состоит в изменении сопротивления проводника при протекании по нему тока из-за его нагрева. При повышении температуры сопротивление проводника увеличивается. Но так как во многих случаях эта зависимость незначительна, элемент считают линейным.

Электрическая цепь, электрическое сопротивление участков которой не зависит от значений и направлений токов и напряжений в цепи, называется линейной электрической цепью. Такая цепь состоит только из линейных элементов, а ее состояние описывается линейными алгебраическими уравнениями.

Если сопротивление элемента цепи существенно зависит от тока или напряжения, то вольт-амперная характеристика носит нелинейный характер, а такой элемент называется нелинейным элементом.

В любой электрической схеме (рис.2.2) различают такие понятия, как точка, ветвь, узел, контур.

Точка – место соединения двух элементов электрической цепи.

Ветвь – участок электрической цепи с одним и тем же током.

 

 

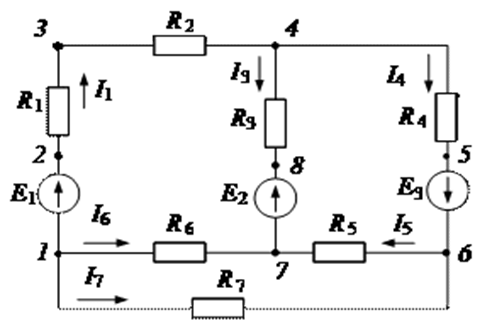
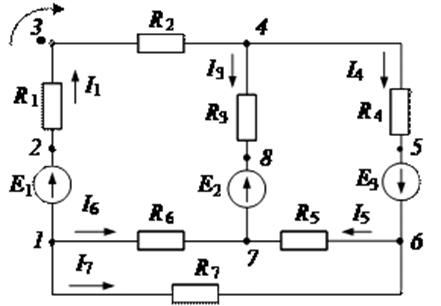
Рис.2.2. Схема электрической цепи

 

 

1, 4, 6, 7 – узлы; 2, 3, 5, 8 – точки соединения элементов; 1–4, 4–6, 4–7, 6–7,

1–7, 1–6 – ветви; 1–4–7–1, 7–4–6–7; 1–7–6–1 - независимые контуры

 

Узел – место соединения трех или более ветвей.

Контур – несколько ветвей, образующих замкнутую цепь.

Независимый контур – это такой, в который входит хотя бы одна ветвь, не входящая в другие контуры.

Элементы электрической цепи постоянного тока характеризуются параметрами:

R – омическое сопротивление – параметр, характеризующий свойства элемента преобразовывать электрическую энергию в другие виды энергии (световую, тепловую, механическую и др.);

Е – электродвижущая сила (ЭДС) – параметр, указывающий на способность элемента создавать и поддерживать разность потенциалов на отдельных участках цепи, а также возбуждать и поддерживать электрический ток в замкнутой цепи.

Элементы электрической цепи делятся на активные и пассивные. К активным элементам относятся те, в которых индуцируется ЭДС (источники ЭДС, электродвигатели, аккумуляторы в процессе зарядки и т. п.). К пассивным элементам относятся электроприемники и соединительные провода.

Резисторы — это элемент, с помощью которых осуществляется регулирование и распределение электрической энергии между цепями и элементами схем. Принцип работы резисторов основан на использовании свойств различных материалов, оказывать сопротивление электрическому току.

Соединение резисторов в различные конфигурации очень часто применяются в электротехнике и электронике.
Здесь мы будем рассматривать только участок цепи, включающий в себя соединение резисторов.
Соединение резисторов может производиться последовательно, параллельно и смешанно (то есть и последовательно и параллельно), что показано на рисунке 1.

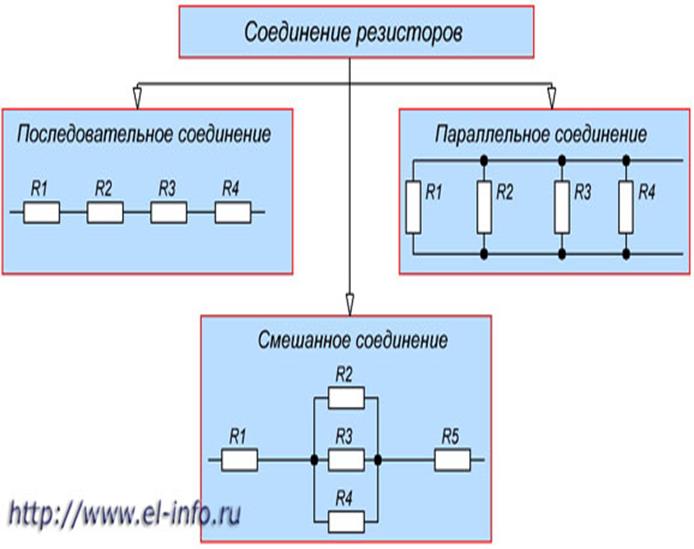
Рисунок 1. Соединение резисторов.

 

Последовательное соединение резисторов это такое соединение, в котором конец одного резистора соединен с началом второго резистора, конец второго резистора с началом третьего и так далее (рисунок 2).

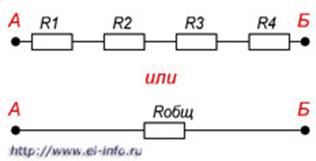
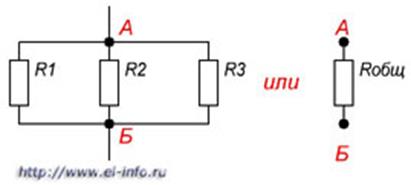
Рисунок 2. Последовательное соединение резисторов.

То есть при последовательном соединении резисторы подключатся друг за другом. При таком соединении через резисторы будет протекать один общий ток.
   Следовательно, для последовательного соединения резисторов будет справедливо сказать, что между точками А и Б есть только один единственный путь протекания тока.
Таким образом, чем больше число последовательно соединенных резисторов, тем большее сопротивление они оказывают протеканию тока, то есть общее сопротивление Rобщ возрастает.
  Рассчитывается общее сопротивление последовательно соединенных резисторов по следующей формуле:

Rобщ = R1 + R2 + R3+...+ Rn.

Параллельное соединение резисторов это соединение, в котором начала всех резисторов соединены в одну общую точку (А), а концы в другую общую точку (Б) (см. рисунок 3).

Рисунок 3. Параллельное соединение резисторов.

 

При этом по каждому резистору течет свой ток. При параллельном соединении при протекании тока из точки А в точку Б, он имеет несколько путей.
Таким образом, увеличение числа параллельно соединенных резисторов ведет к увеличению путей протекания тока, то есть к уменьшению противодействия протеканию тока. А это значит, чем большее количество резисторов соединить параллельно, тем меньше станет значение общего сопротивления такого участка цепи (сопротивления между точкой А и Б.)
Общее сопротивление параллельно соединенных резисторов определяется следующим отношением:

1/Rобщ= 1/R1+1/R2+1/R3+…+1/Rn

Следует отметить, что здесь действует правило «меньше - меньшего». Это означает, что общее сопротивление всегда будет меньше сопротивления любого параллельно включенного резистора.
Общее сопротивление для двух параллельно соединенных резисторов рассчитывается по следующей формуле:

Rобщ= R1*R2/R1+R2

Если имеет место два параллельно соединенных резистора с одинаковыми сопротивлениями, то их общее сопротивление будет равно половине сопротивления одного из них.

Смешанное соединение резисторов является комбинацией последовательного и параллельного соединения. Иногда подобную комбинацию называют последовательно-параллельным соединением.
На рисунке 4 показан простейший пример смешанного соединения резисторов.

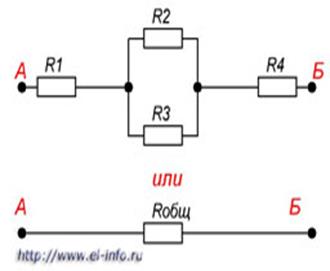
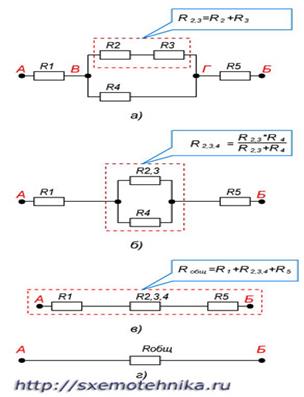
Рисунок 4. Смешанное соединение резисторов.

На этом рисунке видно, что резисторы R2 R3 соединены параллельно, а R1, комбинация R2 R3 и R4 последовательно.
Для расчета сопротивления таких соединений, всю цепь разбивают на простейшие участки, из параллельно или последовательно соединенных резисторов. Далее следуют следующему алгоритму:
1. Определяют эквивалентное сопротивление участков с параллельным соединением резисторов.
2. Если эти участки содержат последовательно соединенные резисторы, то сначала вычисляют их сопротивление.
3. После расчета эквивалентных сопротивлений резисторов перерисовывают схему. Обычно получается цепь из последовательно соединенных эквивалентных сопротивлений.
4. Рассчитывают сопротивления полученной схемы.

Пример расчета участка цепи со смешанным соединением резисторов приведен на рисунке 5.

Рисунок 5. Расчет сопротивления участка цепи при смешанном соединении резисторов.

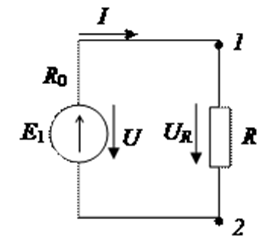
Расчет электрических цепей ведут с помощью основных законов: закона Ома и I и II законов Кирхгофа.

Закон Ома для электрической цепи (рис.2.4).

I = E/ (R ₀ + R).

где R ₀ – внутреннее сопротивление источника питания.

Для участка цепи 1–2;

I = U_R/R.

Рис.2.4. Схема электрической цепи с одним источником питания

 

Первый закон Кирхгофа вытекает из закона сохранения заряда.

Согласно первому закону Кирхгофа (I ЗК), алгебраическая сумма токов ветвей узловой точки равна 0:

 

Рис.2.5. К пояснению Iи II законов Кирхгофа

 

Со знаком «+» принимают притекащие к узлу токи, со знаком «-» – вытекающие (можно наоборот).

Так, для узловой точки 4 (рис.2.5 ):

I ₁ – I ₄ – I ₃ = 0,

 

или сумма притекающих к узлу токов равняется сумме токов, вытекающих из узла:

I ₁ = I ₄ + I ₃.

Второй закон Кирхгофа (II ЗК) является следствием закона сохранения энергии.

Согласно II закону Кирхгофа, в замкнутом контуре электрической цепи алгебраическая сумма ЭДС равна алгебраической сумме напряжений на всех резистивных элементах контура:

Так, для контура 1–4–7–1 запишем II ЗК:

Е ₁ – Е ₂ = I ₁ R ₁ + I ₁ R ₂ + I ₃ R ₃ - I ₆ R ₆,

 

ЭДС, напряжения и токи, направления которых совпадают с направлением обхода контура, например по часовой стрелке, включают в уравнения со знаком «+», а те, которые не совпадают с направлением обхода, – со знаком «-» (можно наоборот).

II ЗК позволяет определить разность потенциалов (напряжение) между любыми двумя точками электрической цепи.

Рассмотрим контур 1-3-4-1. Ветвь 1-4, замыкающая контур, проходит в пространстве, в котором отсутствуют источники питания и резисторы. Примем направление напряжения между точками 1 и 4 от 1 к 4. Тогда по II ЗК справедливо уравнение

Е ₁ = I ₁ R ₁ + I ₁ R ₂ – U ₁₄,

 

откуда напряжение между точками 1 и 4

U ₁₄ = – Е ₁ + I ₁ R ₁ + I ₁ R ₂.

 

Если напряжение U ₁₄ положительно, это означает, что потенциал точки 1 выше потенциала точки 4, и наоборот.

В цепи постоянного тока приемники электрической энергии потребляют активную мощность, которую определяют, умножив правую и левую части формулы на ток I:

I ² = EI /(R ₀ + R),

Откуда EI = I ²(R ₀ + R), или

Р = I ² R ₀ + I ² R,

 

где Р – активная мощность источника питания; I ² R ₀ - потеря мощности в источнике питания; I ² R - мощность, потребляемая электроприемником.