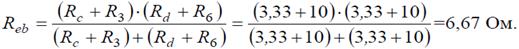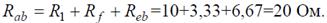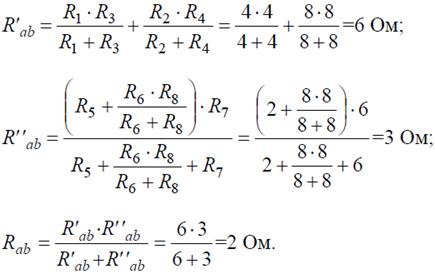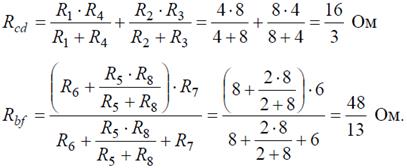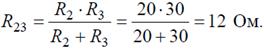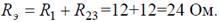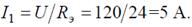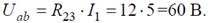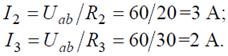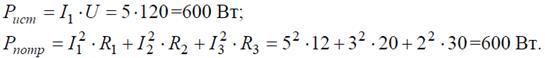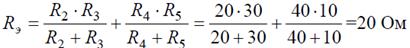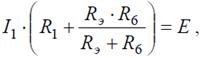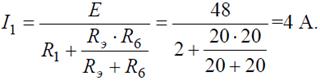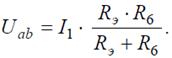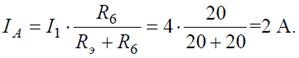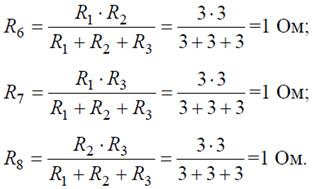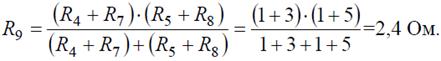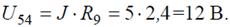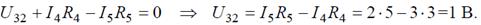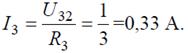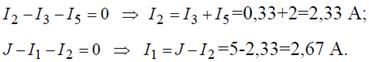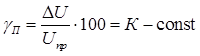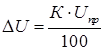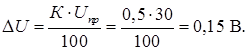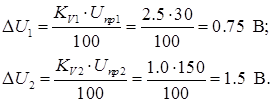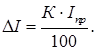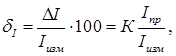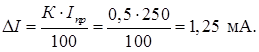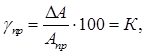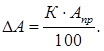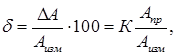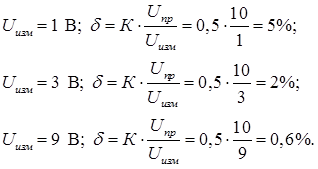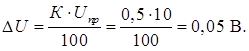Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Электрическая емкость. КонденсаторСодержание книги Поиск на нашем сайте
Практической работе Электрическая емкость. Конденсатор Электрическая емкость (электроемкость) – скалярная физическая величина, характеризующая способность уединенного проводника удерживать электрический заряд. Обозначение – C, единица измерения в СИ – фарад (Ф). Уединенный проводник – это проводник, удаленный от других проводников и заряженных тел. Фарад – электроемкость такого уединенного проводника, потенциал которого изменяется на 1 В при сообщении ему заряда 1 Кл:
Формула для вычисления электроемкости:
где q – заряд проводника, φ – его потенциал. Электроемкость зависит от его линейных размеров и геометрической формы. Электроемкость не зависит от материала проводника и его агрегатного состояния. Электроемкость проводника прямо пропорциональна диэлектрической проницаемости среды, в которой он находится. Конденсатор – это система из двух проводников, разделенных слоем диэлектрика, толщина которого мала по сравнению с размерами проводников. Проводники называют обкладками конденсатора. Заряды обкладок конденсатора равны по величине и противоположны по знаку заряда. Электрическое поле сосредоточено между обкладками конденсатора. Конденсаторы используют для накопления электрических зарядов. Электроемкость конденсатора рассчитывается по формуле:
где q – модуль заряда одной из обкладок, Электроемкость конденсатора зависит от линейных размеров и геометрической формы и расстояния между проводниками. Электроемкость конденсатора прямо пропорциональна диэлектрической проницаемости вещества между проводниками. Плоский конденсатор представляет две параллельные пластины площадью S, находящиеся на расстоянии d друг от друга. Электроемкость плоского конденсатора:
где ε – диэлектрическая проницаемость вещества между обкладками, На электрической схеме конденсатор обозначается:
Виды конденсаторов: · по типу диэлектрика – воздушный, бумажный и т. д.; · по форме – плоский, цилиндрический, сферический; · по электроемкости – постоянной и переменной емкости. Конденсаторы можно соединять между собой.
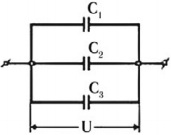
Параллельное соединение конденсаторов
При параллельном соединении конденсаторы соединяются одноименно заряженными обкладками. Напряжения конденсаторов равны:
Общая емкость:
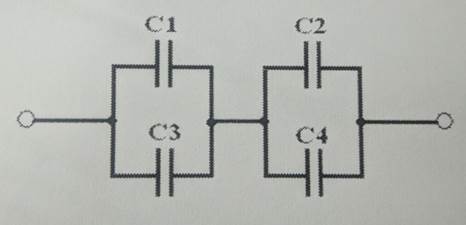
Задачи Определите общую емкость соединения конденсаторов, схема которых приведена на рисунке, если все конденсаторы имеют ёмкость по 10 мкФ
Конденсаторы C₁ и C₃ соединены параллельно, поэтому их заменим на одну емкость C₁₃ C₁,₃ = C₁ + C₃ = 10 + 10 = 20 мкФ Конденсаторы C₂ и C₄ соединены параллельно, поэтому их заменим на одну емкость C₂₄ C₂,₄ = C₂ + C₄ = 10 + 10 = 20 мкФ Теперь емкости C₁₃ и C₂₄ соединены последовательно, поэтому: Cобщ = Cобщ = Определите общую емкость соединения конденсаторов, схема которых приведена на рисунке, если конденсаторы С1С2С3С4 имеют ёмкость по 6 мкФ
Конденсаторы C₁ и C₃ соединены параллельно, поэтому их заменим на одну емкость C₁,2 = C₁ + C2 = 6 + 6= 12 мкФ Теперь емкости C₁,2 и C3 и соединены последовательно, поэтому: C1,2,3 = C1,2,3 = Конденсаторы C₁,2,3 и C4 соединены параллельно C1,2,3,4 = С1,2,3 +С4 =4+6=10 мкф
Определите общую емкость соединения конденсаторов, схема которых приведена на рисунке, если все конденсаторы имеют ёмкость по 3 мкФ
Конденсаторы C₁ и C₃ соединены параллельно, поэтому их заменим на одну емкость C₁₃ C₁₃ = C₁ + C₃ = 10 + 10 = 20 мкФ Конденсаторы C₂ и C₄ соединены параллельно, поэтому их заменим на одну емкость C₂₄ C₂₄ = C₂ + C₄ = 10 + 10 = 20 мкФ Теперь емкости C₁₃ и C₂₄ соединены последовательно, поэтому: Cобщ = Cобщ = Основные элементы цепи. Все электроприемники характеризуются электрическими параметрами, среди которых основные - напряжение и мощность. Для нормальной работы электроприемника на его зажимах необходимо поддерживать номинальное напряжение. Элементы электрической цепи делятся на активные и пассивные. К активным элементам электрической цепи относятся те, в которых индуцируется ЭДС (источники ЭДС, электродвигатели, аккумуляторы в процессе зарядки и т. п.). К пассивным элементам относятся электроприемники и соединительные провода.
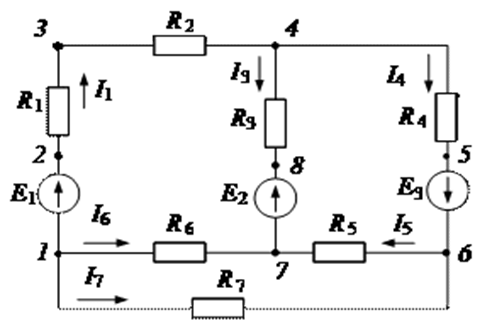
Элементы электрической цепи, обладающие электрическим сопротивлением и называемые резисторами, характеризуются так называемой вольт-амперной характеристикой - зависимостью напряжения на зажимах элемента от тока в нем или зависимостью тока в элементе от напряжения на его зажимах. Если сопротивление элемента постоянно при любом значении тока в нем и любом значении приложенного к нему напряжения, то вольт-амперная характеристика прямая линия и такой элемент называется линейным элементом. В общем случае сопротивление зависит как от тока, так и от напряжения. Одна из причин этого состоит в изменении сопротивления проводника при протекании по нему тока из-за его нагрева. При повышении температуры сопротивление проводника увеличивается. Но так как во многих случаях эта зависимость незначительна, элемент считают линейным. Электрическая цепь, электрическое сопротивление участков которой не зависит от значений и направлений токов и напряжений в цепи, называется линейной электрической цепью. Такая цепь состоит только из линейных элементов, а ее состояние описывается линейными алгебраическими уравнениями. Если сопротивление элемента цепи существенно зависит от тока или напряжения, то вольт-амперная характеристика носит нелинейный характер, а такой элемент называется нелинейным элементом. В любой электрической схеме (рис.2.2) различают такие понятия, как точка, ветвь, узел, контур. Точка – место соединения двух элементов электрической цепи. Ветвь – участок электрической цепи с одним и тем же током.
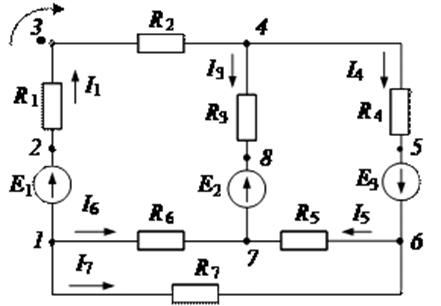
Рис.2.2. Схема электрической цепи
1, 4, 6, 7 – узлы; 2, 3, 5, 8 – точки соединения элементов; 1–4, 4–6, 4–7, 6–7, 1–7, 1–6 – ветви; 1–4–7–1, 7–4–6–7; 1–7–6–1 - независимые контуры
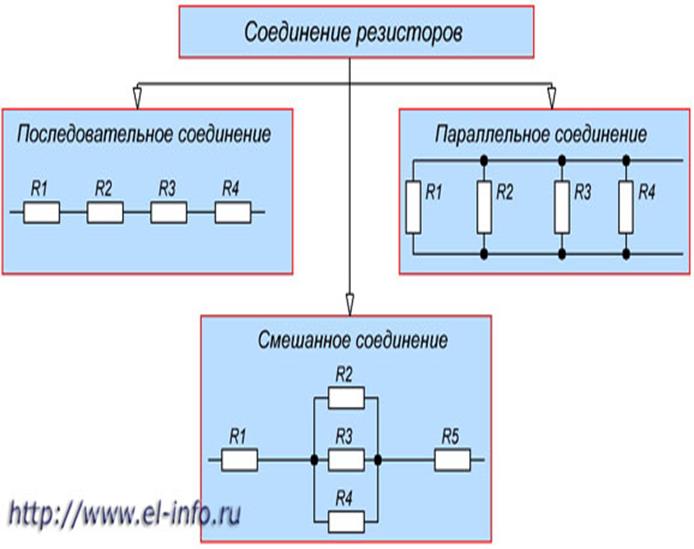
Узел – место соединения трех или более ветвей. Контур – несколько ветвей, образующих замкнутую цепь. Независимый контур – это такой, в который входит хотя бы одна ветвь, не входящая в другие контуры. Элементы электрической цепи постоянного тока характеризуются параметрами: R – омическое сопротивление – параметр, характеризующий свойства элемента преобразовывать электрическую энергию в другие виды энергии (световую, тепловую, механическую и др.); Е – электродвижущая сила (ЭДС) – параметр, указывающий на способность элемента создавать и поддерживать разность потенциалов на отдельных участках цепи, а также возбуждать и поддерживать электрический ток в замкнутой цепи. Элементы электрической цепи делятся на активные и пассивные. К активным элементам относятся те, в которых индуцируется ЭДС (источники ЭДС, электродвигатели, аккумуляторы в процессе зарядки и т. п.). К пассивным элементам относятся электроприемники и соединительные провода. Резисторы — это элемент, с помощью которых осуществляется регулирование и распределение электрической энергии между цепями и элементами схем. Принцип работы резисторов основан на использовании свойств различных материалов, оказывать сопротивление электрическому току. Соединение резисторов в различные конфигурации очень часто применяются в электротехнике и электронике.
Рисунок 1. Соединение резисторов.
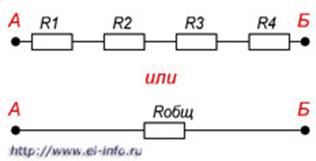
Последовательное соединение резисторов это такое соединение, в котором конец одного резистора соединен с началом второго резистора, конец второго резистора с началом третьего и так далее (рисунок 2).
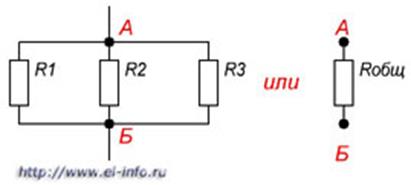
Рисунок 2. Последовательное соединение резисторов. То есть при последовательном соединении резисторы подключатся друг за другом. При таком соединении через резисторы будет протекать один общий ток. Rобщ = R1 + R2 + R3+...+ Rn. Параллельное соединение резисторов это соединение, в котором начала всех резисторов соединены в одну общую точку (А), а концы в другую общую точку (Б) (см. рисунок 3).
Рисунок 3. Параллельное соединение резисторов.
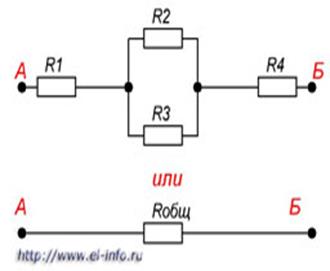
При этом по каждому резистору течет свой ток. При параллельном соединении при протекании тока из точки А в точку Б, он имеет несколько путей. 1/Rобщ= 1/R1+1/R2+1/R3+…+1/Rn Следует отметить, что здесь действует правило «меньше - меньшего». Это означает, что общее сопротивление всегда будет меньше сопротивления любого параллельно включенного резистора. Rобщ= R1*R2/R1+R2 Если имеет место два параллельно соединенных резистора с одинаковыми сопротивлениями, то их общее сопротивление будет равно половине сопротивления одного из них. Смешанное соединение резисторов является комбинацией последовательного и параллельного соединения. Иногда подобную комбинацию называют последовательно-параллельным соединением.
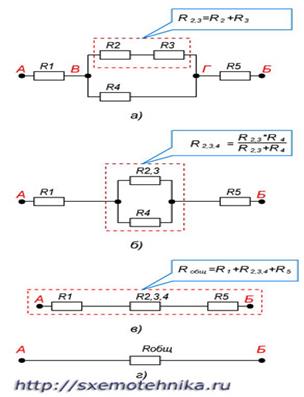
Рисунок 4. Смешанное соединение резисторов. На этом рисунке видно, что резисторы R2 R3 соединены параллельно, а R1, комбинация R2 R3 и R4 последовательно. Пример расчета участка цепи со смешанным соединением резисторов приведен на рисунке 5.
Рисунок 5. Расчет сопротивления участка цепи при смешанном соединении резисторов.
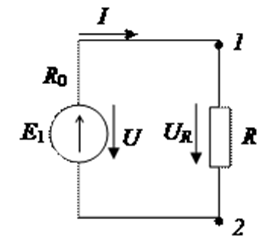
Расчет электрических цепей ведут с помощью основных законов: закона Ома и I и II законов Кирхгофа. Закон Ома для электрической цепи (рис.2.4). I = E/ (R 0 + R). где R 0 – внутреннее сопротивление источника питания. Для участка цепи 1–2; I = UR/R.
Рис.2.4. Схема электрической цепи с одним источником питания
Первый закон Кирхгофа вытекает из закона сохранения заряда. Согласно первому закону Кирхгофа (I ЗК), алгебраическая сумма токов ветвей узловой точки равна 0:
Рис.2.5. К пояснению Iи II законов Кирхгофа
Со знаком «+» принимают притекащие к узлу токи, со знаком «-» – вытекающие (можно наоборот). Так, для узловой точки 4 (рис.2.5 ): I 1 – I 4 – I 3 = 0,
или сумма притекающих к узлу токов равняется сумме токов, вытекающих из узла: I 1 = I 4 + I 3. Второй закон Кирхгофа (II ЗК) является следствием закона сохранения энергии. Согласно II закону Кирхгофа, в замкнутом контуре электрической цепи алгебраическая сумма ЭДС равна алгебраической сумме напряжений на всех резистивных элементах контура:
Так, для контура 1–4–7–1 запишем II ЗК: Е 1 – Е 2 = I 1 R 1 + I 1 R 2 + I 3 R 3 - I 6 R 6,
ЭДС, напряжения и токи, направления которых совпадают с направлением обхода контура, например по часовой стрелке, включают в уравнения со знаком «+», а те, которые не совпадают с направлением обхода, – со знаком «-» (можно наоборот). II ЗК позволяет определить разность потенциалов (напряжение) между любыми двумя точками электрической цепи. Рассмотрим контур 1-3-4-1. Ветвь 1-4, замыкающая контур, проходит в пространстве, в котором отсутствуют источники питания и резисторы. Примем направление напряжения между точками 1 и 4 от 1 к 4. Тогда по II ЗК справедливо уравнение Е 1 = I 1 R 1 + I 1 R 2 – U 14,
откуда напряжение между точками 1 и 4 U 14 = – Е 1 + I 1 R 1 + I 1 R 2.
Если напряжение U 14 положительно, это означает, что потенциал точки 1 выше потенциала точки 4, и наоборот. В цепи постоянного тока приемники электрической энергии потребляют активную мощность, которую определяют, умножив правую и левую части формулы на ток I: I 2 = EI /(R 0 + R), Откуда EI = I 2(R 0 + R), или Р = I 2 R 0 + I 2 R,
где Р – активная мощность источника питания; I 2 R 0 - потеря мощности в источнике питания; I 2 R - мощность, потребляемая электроприемником.
Решение Исходную схему можно перечертить относительно входных зажимов (рис. 2, б), из чего видно, что все сопротивления включены параллельно. Так как величины сопротивлений равны, то для определения величины эквивалентного сопротивления можно воспользоваться формулой:
n – количество параллельно соединенных сопротивлений.
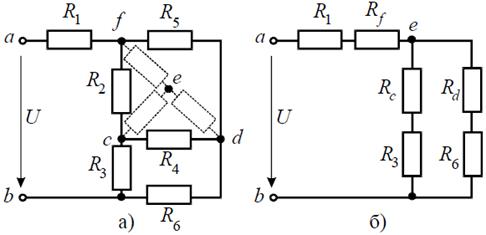
Задача 3. Определить эквивалентное сопротивление относительно зажимов a–b, если R 1 = R 2 = R 3 = R 4 = R 5 = R 6 = 10 Ом (рис. 3, а).
Рис. 3 Решение Преобразуем соединение «треугольник» f−d−c в эквивалентную «звезду». Определяем величины преобразованных сопротивлений (рис. 3, б):
И тогда эквивалентное сопротивление исходной схемы представляет последовательное соединение сопротивлений:
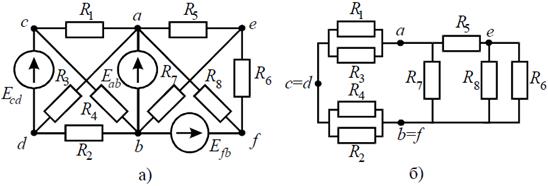
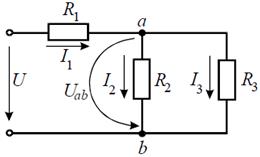
Задача 4. В заданной цепи (рис. 4, а) определить методом эквивалентных преобразований входные сопротивления ветвей a−b, c–d и f−b, если известно, что: R 1 = 4 Ом, R 2 = 8 Ом, R 3 =4 Ом, R 4 = 8 Ом, R 5 = 2 Ом, R 6 = 8 Ом, R 7 = 6 Ом, R 8 =8 Ом. Решение Для определения входного сопротивления ветвей исключают из схемы все источники ЭДС. При этом точки c и d, а также b и f соединяются накоротко, т.к. внутренние сопротивления идеальных источников напряжения равны нулю.
Рис. 4 Ветвь a−b разрывают, и т.к. сопротивление Ra–b = 0, то входное сопротивление ветви равно эквивалентному сопротивлению схемы относительно точек a и b (рис. 4, б):
Аналогично методом эквивалентных преобразований определяются входные сопротивления ветвей Rcd и Rbf. Причем, при вычислении сопротивлений учтено, что соединение накоротко точек a и b исключает («закорачивает») из схемы сопротивления R 1, R 2, R 3, R 4 в первом случае, и R 5, R 6, R 7, R 8 во втором случае.
Задача 5. В цепи (рис. 5) определить методом эквивалентных преобразований токи I 1, I 2, I 3и составить баланс мощностей, если известно: R 1 = 12 Ом, R 2 = 20 Ом, R 3 = 30 Ом, U = 120 В.
Рис. 5 Решение Эквивалентное сопротивление для параллельно включенных сопротивлений:
Эквивалентное сопротивление всей цепи:
Ток в неразветвленной части схемы:
Напряжение на параллельных сопротивлениях:
Токи в параллельных ветвях:
Баланс мощностей:
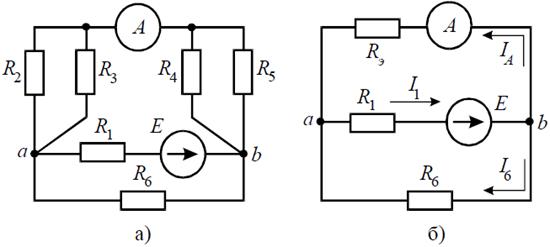
Задача 6. В цепи (рис. 6, а), определить методом эквивалентных преобразований показания амперметра, если известно: R 1 = 2 Ом, R 2 = 20 Ом, R 3 = 30 Ом, R 4 = 40 Ом, R 5 = 10 Ом, R 6 = 20 Ом, E = 48 В. Сопротивление амперметра можно считать равным нулю.
Рис. 6 Решение Если сопротивления R 2, R 3, R 4, R 5 заменить одним эквивалентным сопротивлением RЭ, то исходную схему можно представить в упрощенном виде (рис. 6, б). Величина эквивалентного сопротивления:
Преобразовав параллельное соединение сопротивлений RЭ и R 6 схемы (рис. 6, б), получим замкнутый контур, для которого по второму закону Кирхгофа можно записать уравнение:
откуда ток I 1:
Напряжение на зажимах параллельных ветвей Uab выразим из уравнения по закону Ома для пассивной ветви, полученной преобразованием RЭ и R 6:
Тогда амперметр покажет ток:
Задача 7. Определить токи ветвей схемы методом эквивалентных преобразований (рис. 7, а), если R 1 = R 2 = R 3 = R 4 = 3 Ом, J = 5 А, R 5 = 5 Ом.
Рис. 7 Решение Преобразуем «треугольник» сопротивлений R 1, R 2, R 3 в эквивалентную «звезду» R 6, R 7, R 8 (рис. 7, б) и определим величины полученных сопротивлений:
Преобразуем параллельное соединение ветвей между узлами 4 и 5
Ток в контуре, полученном в результате преобразований, считаем равным току источника тока J, и тогда напряжение:
И теперь можно определить токи I 4 и I 5:
Возвращаясь к исходной схеме, определим напряжение U 32 из уравнения по второму закону Кирхгофа:
Тогда ток в ветви с сопротивлением R 3 определится:
Величины оставшихся неизвестными токов можно определить из уравнений по первому закону Кирхгофа для узлов 3 и 1:
Примеры решения задач Задача №1 Определить для вольтметра с пределом измерения 30 В класса точности 0,5 относительную погрешность для точек 5, 10, 15, 20, 25 и 30 В и наибольшую абсолютную погрешность прибора. Решение 1. Класс точности указывают просто числом предпочтительного рода, например, 0,5. Это используют для измерительных приборов, у которых предел допускаемой приведенной погрешности постоянен на всех отметках рабочей части его шкалы (присутствует только аддитивная погрешность). Таким способом обозначают классы точности вольтметров, амперметров, ваттметров и большинства других однопредельных и многопредельных приборов с равномерной шкалой. Приведенная погрешность (выраженное в процентах отношение абсолютной погрешности к нормирующему значению)
постоянна и равна классу точности прибора. Относительная погрешность однократного измерения (выраженное в процентах отношение абсолютной погрешности к истинному значению измеряемой величины)
уменьшается к значению класса точности прибора с ростом измеренного значения к предельному значению шкалы прибора. Абсолютная погрешность однократного измерения
постоянна на всех отметках рабочей части шкалы прибора. По условию задачи: Uизм = Ui = 5, 10, 15, 20, 25 и 30 В – измеренное значение электрической величины; Uпр = 30 В – предел шкалы вольтметра. 2. Приведенная погрешность
3. Наибольшая абсолютная погрешность вольтметра
4. Относительная погрешность вольтметра для точек
Задача №2 При измерении напряжения двумя параллельно включенными вольтметрами их показания были: U 1 = 29,2 В, U 2 = 30 В. Показания какого прибора точнее, если класс точности КV 1 = 2,5, КV 2 = 1,0, а пределы измерения соответственно равны Uпр 1 = 30 В; Uпр 2 = 150 В. Решение Класс точности указывают просто числом предпочтительного рода, например, 0,05. Это используют для измерительных приборов, у которых предел допускаемой приведенной погрешности постоянен на всех отметках рабочей части его шкалы (присутствует только аддитивная погрешность). Тогда абсолютные погрешности измерения напряжения вольтметрами
Более точным будет первый вольтметр.
Задача №3 Ток 159 мА измеряется цифровым вольтметром с трехразрядным цифровым индикатором и амперметром с классом точности 0,5 и пределом шкалы 250 мА. Каким прибором ток будет измерен точнее? Решение Абсолютная погрешность однократного измерения амперметром
где Iпр – измеренное значение электрической величины; К – класс точности прибора. Относительная погрешность однократного измерения амперметром
где Iизм – предел шкалы амперметра. В задаче наряду с аналоговым измерительным прибором используется цифровой. Абсолютная погрешность Δ I цифрового прибора принимается равной единице младшего разряда числа, высвечиваемого на цифровом индикаторе. Класс точности аналогового амперметра пределом шкалы Iпр = 250 мА выражается одним числом К = 0,5. Оценка погрешности однократного измерения аналогового амперметра
Ток Iизм = 159 мА измеряется цифровым вольтметром с трехразрядным цифровым индикатором. Абсолютную погрешность Δ I цифрового прибора принимается равной единице младшего разряда числа, высвечиваемого на цифровом индикаторе: Δ I = 1 мА. Откуда, абсолютная погрешность цифрового амперметра меньше чем аналогового. Следовательно, цифровой вольтметр точнее измеряет ток Iизм = 159 мА. Задача №4 Значения класса точности аналогового вольтметра К = 0,5. Какой будет относительная и абсолютная погрешности однократных измерений напряжения Uизм = 1; 3; 9 В на пределе измерения Uпр = 10 В? Решение Класс точности прибора выражается одним числом К. Предельная погрешность
где Δ A – абсолютная погрешность, Aпр – предел шкалы измерительного прибора. Для оценки погрешности однократного измерения полагаем абсолютную погрешность
Относительная погрешность однократного измерения
где Aизм – измеренное значение электрической величины. Класс точности аналогового вольтметра с пределом шкалы Uпр = 10 В при измерении постоянного напряжения выражается одним числом К = 0,5. Относительная погрешность однократных измерений напряжения Uизм = 1; 3; 9 В:
Абсолютная погрешность однократных измерений напряжения Uизм = 1; 3; 9 В:
Запишем результаты измерений напряжений Uизм =1; 3; 9 В: Uизм = 1,0 ± 0,05 В или Uизм = 1,0 В ± 5 %; Uизм = 3,0 ± 0,05 В или Uизм = 3,0 В ± 2 %; Uизм = 9,0 ± 0,05 В или Uизм = 9,0 В ± 0,6 %. Контрольно-оценочные средства включают в себя выполнение практической работы, в которую входят 3 задания. Каждое задание содержит 5 вариантов. Задания 1–решение задачи согласно своему варианту Задания 2–решение задачи согласно своему варианту Задания 3–решение задачи согласно своему варианту По итогу оценивания практической работы– бальное с переводом в традиционную пятибалльную. Шкала оценивания: максимальное количество баллов – 15 3 задания – оценка «5»; 2 задания – оценка «4»; 1 задание – оценка «3»; При выставлении экзаменационной оценки по дисциплине ОП.1 Электротехника в экзаменационную ведомость (протокол) выставляется оценка, рассчитанная по формуле: 𝑵=𝒏т.у.+𝒏с.р.+𝒏т.з.𝟑, где 𝑛т.у. – средняя оценка текущей аудиторной успеваемости; 𝑛к.р. - оценка за самостоятельную работу; 𝑛т.з. - оценка за итоговую практическую работу
Практической работе Электрическая емкость. Конденсатор Электрическая емкость (электроемкость) – скалярная физическая величина, характеризующая способность уединенного проводника удерживать электрический заряд. Обозначение – C, единица измерения в СИ – фарад (Ф). Уединенный проводник – это проводник, удаленный от других проводников и заряженных тел. Фарад – электроемкость такого уединенного проводника, потенциал которого изменяется на 1 В при сообщении ему заряда 1 Кл:
Формула для вычисления электроемкости:
где q – заряд проводника, φ – его потенциал. Электроемкость зависит от его линейных размеров и геометрической формы. Электроемкость не зависит от материала проводника и его агрегатного состояния. Электроемкость проводника прямо пропорциональна диэлектрической проницаемости среды, в которой он находится. Конденсатор – это система из двух проводников, разделенных слоем диэлектрика, толщина которого мала по сравнению с размерами проводников. Проводники называют обкладками конденсатора. Заряды обкладок конденсатора равны по величине и противоположны по знаку заряда. Электрическое поле сосредоточено между обкладками конденсатора. Конденсаторы используют для накопления электрических зарядов. Электроемкость конденсатора рассчитывается по формуле:
где q – модуль заряда одной из обкладок, Электроемкость конденсатора зависит от линейных размеров и геометрической формы и расстояния между проводниками. Электроемкость конденсатора прямо пропорциональна диэлектрической проницаемости вещества между проводниками. Плоский конденсатор представляет две параллельные пластины площадью S, находящиеся на расстоянии d друг от друга. Электроемкость плоского конденсатора:
где ε – диэлектрическая проницаемость вещества между обкладками, На электрической схеме конденсатор обозначается:
Виды конденсаторов: · по типу диэлектрика – воздушный, бумажный и т. д.; · по форме – плоский, цилиндрический, сферический; · по электроемкости – постоянной и переменной емкости. Конденсаторы можно соединять между собой.
|
|||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-06-14; просмотров: 170; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.109.152 (0.017 с.) |

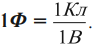
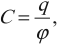
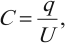

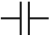
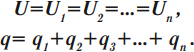
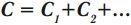
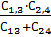
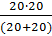 =10 мкф
=10 мкф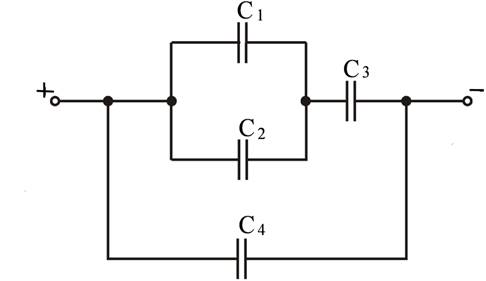
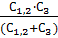
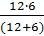 =4мкф
=4мкф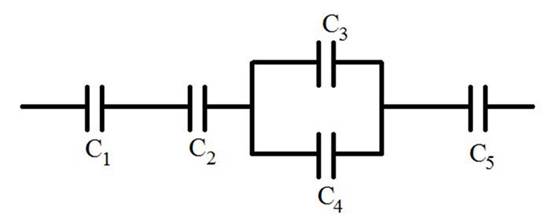
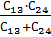



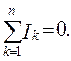

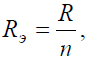 где R – величина сопротивления, Ом;
где R – величина сопротивления, Ом;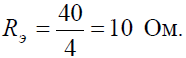
 По условию задачи величины всех сопротивлений равны, а значит:
По условию задачи величины всех сопротивлений равны, а значит: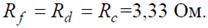 На преобразованной схеме получили параллельное соединение ветвей между узлами e–b, тогда эквивалентное сопротивление равно:
На преобразованной схеме получили параллельное соединение ветвей между узлами e–b, тогда эквивалентное сопротивление равно: