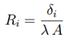Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тепловое моделирование кондуктивно-лучистого теплообменаСодержание книги
Поиск на нашем сайте
При моделировании лучистого теплообмена рассматривают 3 класса задач: 1. Излучение в окружающую среду 2. Излучение с поверхности на поверхность в диатермических (прозрачных) средах 3. Перенос тепла излучением в недиатермических средах. Когда учитывают лучистый теплообмен: · Прозрачные и полупрозрачные среды · Высокие значение коэффициента излучения · Большая разность температур между излучающими поверхностями · Внешние источники излучения · При низкой интенсивности теплопроводности/конвекции · На малых временных масштабах Варианты описания свойств поверхностей (варианты граничных условий при моделировании теплообмена с поверхности на поверхность): Основное граничное условие – диффузно-излучающая и отражающая поверхность
где J – энергетическая светимость, У диффузно-отражающей поверхности В случае серой поверхности используется уравнение Стефана-Больцмана для серого тела. Для диффузно-зеркального отражения добавляется связь Для учёта и диффузного, и зеркального отражения и пропускания (
Энергетическая светимость определяется для двух сторон выбранных поверхностей, поскольку излучение может идти в обе стороны от поверхности. В простейшем случае стационарной теплопроводности в твердом теле
Уравнение дополняется условиями однозначности: краевыми условиями. Уравнение теплопроводности в нестационарных задачах:
При рассмотрении систем уравнений с весьма общими краевыми условиями точные методы решения наталкиваются на большие трудности, почти непреодолимые при рассмотрении нелинейных задач. В этих случаях используют численные методы решения. Использование таких методов позволяет отказаться от упрощённой трактовки математической модели процесса. К нелинейной постановке задач теплопроводности приводят: · Зависимость коэффициентов (теплофизических свойств) и правой части (мощности тепловыделения) уравнения от температуры.
· Нелинейность краевых условий · Зависимость коэффициентов, мощности или краевых условий от переменных, входящих в дифференциальные уравнения, описывающие другие физические процессы. Граничные условия 1, 2 и 3го рода были рассмотрены выше. В нестационарных задачах в качестве начальных условий необходимо задать распределение температуры в расчетной области в начальный момент времени
Начальные условия должны соответствовать заданным граничным условиям. Симметрия и периодические граничные условия в моделировании позволяют сократить используемые ресурсы и время счета благодаря уменьшению размера расчетной области. Симметрией (периодичностью) должна обладать не только геометрия модели, но и граничные, начальные условия, свойства материалов. При задании ГУ 3 рода требуется величина теплоотдачи.
Фактически, в этом случае мы исключаем движущуюся среду из расчётной области, описывая теплообмен с ней через ГУ 3 рода. Коэффициент теплоотдачи α – гидродинамический параметр. В САПР COMSOL имеются встроенные соотношения для расчёта коэффициента теплоотдачи при внешнем обтекании и при течении в каналах. При постановке ГУ 3 рода могут потребоваться метеорологические данные (температура, давление, скорость ветра, интенсивность солнечного излучения) Источники теплоты могут быть заданы пользовательскими соотношениями, либо рассчитаны с помощью теплофизических интерфейсов (рис. 4.12).
Рисунок 4.12 Теплофизические интерфейсы в САПР COMSOL Теплофизические свойства материалов могут быть как заданы вручную, так и загружены из базы данных (библиотеки материалов). Свойства могут быть заданы в виде: · Постоянных значений · Аналитических функций · Интерполяционных таблиц · Кусочно-заданных полиномов Для материалов с анизотропными свойствами коэффициент теплопроводности может быть задан в виде вектора или тензора:
КА состоит из двух частей — геометрической и тепловой. Геометрическая часть модели представляет собой набор плоских выпуклых многоугольников, моделирующих поверхности каркаса и оборудования КА. Такое геометрическое представление конструкции предназначено в первую очередь для определения внешних тепловых потоков, падающих на поверхности КА и уходящих с них, включая взаимное отражение между частями КА. При расчете внешних потоков учитываются: прямой поток электромагнитной энергии от Солнца, отраженный от Земли поток солнечного излучения, инфракрасный поток от Земли [15]. Тепловая часть модели — это совокупность элементов, тепловых связей между элементами, нагревателей и источников тепловыделения. Элементы представляют собой сосредоточенную теплоемкость и имеют в каждый момент времени одно значение температуры. В связи с большим числом элементов таблица с их рассчитанными теплоемкостями не приведена. Тепловые связи делятся на два типа: линейные и нелинейные. Линейные связи используются для учета кондуктивного и конвективного теплообмена между элементами тепловой математической модели (ТММ), нелинейные — для учета лучистого теплообмена между элементами ТММ. Некоторые элементы ТММ имеют источники тепловыделения. Тепловыделение в элементах служит для моделирования работы приборов и двигателей КА. В ТММ КА нагреватели моделируются как управляемые источники теплоты — нагреватель передает теплоту заданному элементу только тогда, когда температура элемента (датчика) опускается ниже температуры включения. Когда температура на элементе (датчике) становится больше температуры выключения, нагреватель перестает выделять теплоту. При нахождении на орбите КА подвергается воздействию переменным по времени внешним тепловым потокам от Солнца и Земли, а также воздействию солнечного теплового потока, отраженного от планеты. Тепловой поток от Солнца определяется взаимной ориентацией Солнца и плоскостей КА, а также изменением в течение года солнечной постоянной. Минимальные внешние условия (1 июля): угол между плоскостью орбиты и направлением на Солнце 17◦; поток составляет 1320 Вт/м2. Максимальные внешние условия (1 февраля): угол между плоскостью орбиты и направлением на Солнце 27◦; тепловой поток составляет 1420 Вт/м2. Инфракрасный поток от Земли определяется средней радиационной температурой планеты: минимальные условия — поток составляет 200 Вт/м2; максимальные условия — поток составляет 240 Вт/м2. Параметры тепловой модели: 1. Линейные тепловые связи. В данной модели можно выделить основные виды тепловых кондуктивных связей между граничащими элементами: • листа обшивок панелей; • сотовых панелей; • листа обшивки и сот; • листа обшивки и тепловой трубы (ТТ); • листа обшивки и КТТ; • листа обшивка и некоторого прибора. Кондуктивная тепловая связь определялась по выражению
где К – значение связи, R0 – контактное термическое сопротивление, R1, R2 – термические сопротивления со стороны первого и второго элементов. Коэффициент теплопроводности алюминия равен 120 Вт/(м∙K). Термические сопротивления вычислялись по формуле
где Ri — термическое сопротивление; δi — расстояние от центра масс элемента до зоны контакта; λi — коэффициент теплопроводности; Ai — площадь теплового контакта. 2.Связи между элементами обшивок. Элемент обшивки представляет собой прямоугольный параллелепипед. Контактное сопротивление отсутствует: R0 = 0. Формула для расчета тепловой связи примет вид
где δi — расстояние от центра масс элемента до центра контактной площадки; λ — коэффициент теплопроводности; A — площадь теплового контакта. 3.Связи между элементами сот. Технология производства сотовых панелей такова, что тепловые кондуктивные связи при расчете “вдоль” и “поперек” панели будут различными/ 4.Связи между элементами листа обшивки и сот. Элемент обшивки представляет собой прямоугольный параллелепипед. Контактное сопротивление также отсутствует, т.е. R0 = 0. Формулы для расчета тепловой связи и термического сопротивления аналогичны приведенным в п. 2. Для определения фактической площади теплового контакта со стороны элемента сот вводится коэффициент сот — отношение фактической площади сот к площади обшивки. 5.Связи между элементами листа обшивка и элементом, моделирующим некоторый прибор. При расчете связей этой группы учитывается только контактное сопротивление термопасты: R1 = R2 = 0. 6.Связи между элементом обшивки и элементом ТТ. Элементы обшивки представляют собой прямоугольные параллелепипеды, элемент ТТ геометрии не имеет. Контактное сопротивление мало и не учитывается, т.е. R0 = 0.
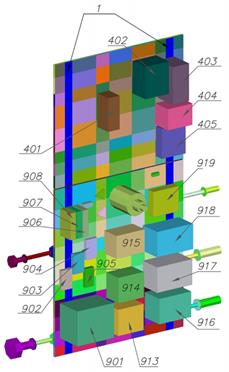
Рисунок 4.13 Моделирование приборов КА на тепловых панелях Гипертеплопроводящая панель представляет собой плоскую тепловую трубу и является устройством, обеспечивающим эффективную интенсивность теплопередачи, многократно превышающую аналогичные показатели металлов. Перенос тепла по панели осуществляется за счет движения теплоносителя в виде пара от области нагрева к области конденсации по паровым каналам и обратно в виде жидкости по фитилю за счет капиллярных сил. Большая величина скрытой теплоты парообразования обеспечивает высокую эффективную теплопроводность панели. В данной работе представлена двумерная стационарная математическая модель теплообмена в ГТП-панели. На основе модели описан алгоритм оценки работоспособности панели по капиллярному ограничению для заданного распределения тепловой нагрузки на поверхность. Модель позволяет получить температурное поле поверхности панели [16]. Панель представляет собой плоскую тонкую герметичную конструкцию, содержащую фитиль, заполненный теплоносителем (аммиак, вода и т. п.), и каналы для переноса пара (рис. 4.14).
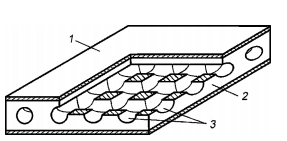
Рисунок 4.14 Структура ГТП-панели 1 — корпус, 2 — фитиль, 3 — паровые каналы Работоспособность панели для заданного распределения тепловой нагрузки на поверхность зависит от возможности капиллярной структуры доставить жидкий теплоноситель к областям нагрева. Иными словами, капиллярный напор фитиля должен превышать сумму падений давлений в жидкости, движущейся по фитилю, и в паре, движущемся по паровым каналам. Предложенная математическая модель основана на проверке выполнения указанного капиллярного ограничения. Работоспособность панели для заданного распределения тепловой нагрузки на поверхность зависит от возможности капиллярной структуры доставить жидкий теплоноситель к областям нагрева. Иными словами, капиллярный напор фитиля должен превышать сумму падений давлений в жидкости, движущейся по фитилю, и в паре, движущемся по паровым каналам. Предложенная математическая модель основана на проверке выполнения указанного капиллярного ограничения. Выводы. 1. Описаны методы теплового моделирования. 2. Рассмотрены пакеты прикладных программ для теплового моделирования космических изделий. 3. Рассмотрены особенности теплового моделирования кондуктивно-лучистого теплообмена.
Список рисунков Рисунок 1.1 Зависимость коэффициента теплопроводности от температуры меди....................... 5 Рисунок 1.2 Зависимость коэффициента теплопроводности от температуры стали 12X18H10T 5 Рисунок 1.3 Зависимость коэффициента теплопроводности от температуры АМг6..................... 6 Рисунок 1.4 Зависимость коэффициента теплопроводности от температуры ВТ1- 0.................... 6 Рисунок 1.5 Теплопроводность прессованной древесины вдоль и поперек волокон в зависимости от объёмного веса и температуры............................................................................................................. 7 Рисунок 1.6 Зависимость коэффициента теплопроводности от температуры для текстолита...... 7 Рисунок 2.1 Фрагмент процесса укрывания корпусного модуля ЭВТИ........................................ 12 Рисунок 2.2 Зависимость плотности теплового потока имитатора-излучателя от напряжения питания, подаваемого на имитатор-излучатель................................................................................................ 13 Рисунок 2.3 Изменение во времени плотности теплового потока, проходящего через ЭВТИ двигателя 13 Рисунок 2.4 Высота полета, тепловой поток в точке торможения, температура оболочки бака окислителя (горючего) в зависимости от времени при спуске РБФ с ССО....................................................... 14 Рисунок 3.1 Профиль шероховатости поверхности и обозначения его характеристик............... 15 Рисунок 3.2 График зависимости теплового контактного сопротивления от усилия сжатия. Прокладка - дюралюминиевая или медная фольга................................................................................................. 19 Рисунок 3.3 Зависимость КТС от силы сжатия, шероховатости и твердости соприкасающихся поверхностей для пары медь-медь............................................................................................................................... 19 Рисунок 3.4 Схема тепловой трубы.................................................................................................... 21 Рисунок 3.5 Распределение давления в паре и жидкости по длине тепловой трубы (зона испарения, адиабатическая зона и зона конденсации)......................................................................................... 22 Рисунок 3.6 Зависимость перепада температуры вдоль направления теплопереноса и эффективный коэффициент теплопроводности в зависимости от температуры области теплоотвода.............. 23 Рисунок 3.7 Проволочная конструкция термометра сопротивления............................................. 26 Рисунок 3.8 Пленочный термометр сопротивления......................................................................... 27 Рисунок 3.9 Зависимость сопротивления ПТС (Pt100) от температуры........................................ 28 Рисунок 3.10 Зависимость термоэлектродвижущей силы (ТЭДС) термопар от температуры.... 29 Рисунок 3.11 Конструкция термопары.............................................................................................. 30 Рисунок 3.12 Способы заделки горячего спая термопары............................................................... 32 Рисунок 4.1 Классификация систем обеспечения тепловых режимов........................................... 34 Рисунок 4.2 Принципиальная технологическая схема СТР............................................................ 34 Рисунок 4.3 Элемент конструкции РТ............................................................................................... 35 Рисунок 4.4 Прямоугольная сетка для двумерной задачи................................................................ 37 Рисунок 4.5 Сетка из прямоугольных параллелепипедов для трехмерной задачи....................... 38 Рисунок 4.6 Аппроксимирующие функции...................................................................................... 39 Рисунок 4.7 Структурированная сетка контрольных объемов с «привязкой» переменных к центру ячеек................................................................................................................................................................ 40 Рисунок 4.8 Рассматриваемое в примере твердое тело.................................................................... 42 Рисунок 4.9 Рассчитанные значения температуры внешней обшивки КА................................... 45 Рисунок 4.10 Пример расчёта в SolidWorks Simulation.................................................................... 46 Рисунок 4.11 Пример теплового анализа с помощью инструментов модуля теплопередача в Comsol Multiphysics............................................................................................................................................ 48 Рисунок 4.12 Теплофизические интерфейсы в САПР COMSOL.................................................... 50 Рисунок 4.13 Моделирование приборов КА на тепловых панелях................................................ 53 Рисунок 4.14 Структура ГТП-панели................................................................................................. 54 Список таблиц Таблица 1.1 Коэффициенты теплопроводностей конструкционных материалов.......................... 4 Таблица 1.2 Значения тепловых потоков и их плотностей............................................................... 4 Таблица 3.1 Параметры шероховатости............................................................................................. 15 Таблица 3.2 Значение параметров шероховатости для классов...................................................... 16 Таблица 3.3 Шероховатость в зависимости от класса обработки................................................... 18 Таблица 3.4 Основные параметры и результаты испытаний НТТ.................................................. 24 Таблица 3.5 Основные параметры и результаты испытаний ВТТ.................................................. 25 Таблица 3.6 Свойства металлов для чехлов термопар...................................................................... 30 Список источников 1. С. В. ЦАПЛИН, С.А. БОЛЫЧЕВ, А.Е. РОМАНОВ ТЕПЛООБМЕН В КОСМОСЕ с.9,14, 66-70. 2. А.В. Муратов Н.В. Ципина СПОСОБЫ ОБЕСПЕЧЕНИЯ ТЕПЛОВЫХ РЕЖИМОВ с. 6-7 3. Система терморегулирования пилотируемого орбитального космического аппарата с парокомпрессионной холодильной машиной А.И. Смородин, И.Е. Меньщиков, С.А. Гаранов, с.26-27 4. А. С. Ртищева Методы моделирования теплоэнергетических процессов с.8-10 5. Математическое моделирование тепловых режимов космических аппаратов негерметичного исполнения С. В. Лемешевский, М. М. Чуйко, А. И. Шнип, Г. Л. Марцинкевич, В. В. Лепин, В. А. Ирхин с.26-27 6. ОСНОВЫ МЕТОДА КОНЕЧНЫХ ЭЛЕМЕНТОВ Л.Е. КОНДРАТЬЕВА с.3-5 7. Е.М. Смирнов, Д.К. Зайцев МЕТОД КОНЕЧНЫХ ОБЪЕМОВ В ПРИЛОЖЕНИИ К ЗАДАЧАМ ГИДРОГАЗОДИНАМИКИ И ТЕПЛООБМЕНА В ОБЛАСТЯХ СЛОЖНОЙ ГЕОМЕТРИИ с. 4-5 8. Тепломассообмен в энергетических установках А.П.Солодов ч.1 гл.3 с. 2-4 9. ПОСТАНОВКА ЗАДАЧИ МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ ТЕПЛОВОГО И ЭЛЕКТРИЧЕСКОГО ПОЛЕЙ ЭЛЕКТРОЛИЗЕРА Смирнов г.б. с.144-145 10. Деревянко В. А. Нестеров Д. А. Косенко В. Е. ПЛОСКИЕ ТЕПЛОВЫЕ ТРУБЫ ДЛЯ ОТВОДА ТЕПЛА ОТ ЭЛЕКТРОННОЙ АППАРАТУРЫ В КОСМИЧЕСКИХ АППАРАТАХ с.116 11. Технологические основы тепловых труб/Ивановский М. Н., Сорокин В. П. 12. Анатолий Андрусевич Термометры сопротивления: от теории к практике с.61-63 13. Ю.И.Агеенко, Р.Н.Гальперин ИССЛЕДОВАНИЕ ВЛИЯНИЯ ТЕПЛОВОГО ПОТОКА ОТ МАРШЕВОГО ЖРД, НА ПАРАМЕТРЫ УПРАВЛЯЮЩИХ ЖРДМТ В УСЛОВИЯХ, ДВИГАТЕЛЬНОЙ УСТАНОВКИ ПЕРСПЕКТИВНОГО РАЗГОННОГО БЛОКА с. 253 14. Расчет элементов оборудования космических аппаратов Бугрова А.Д. с.13-14 15. ИССЛЕДОВАНИЕ ТЕПЛОВОГО СОСТОЯНИЯ МАЛОГО КОСМИЧЕСКОГО АППАРАТА П.Д. Судомоин, В.А. Шабанов, К.А. Платонов, С.И. Каськов с. 31-38 16. Вычислительное моделирование процессов теплообмена в системах терморегулирования космических аппаратов Е. Н. Васильев, В. А. Деревянко с.23-24 17. ОСТ 92-4269-74. (б.д.). Термометры сопротивления и термометры термоэлектрические. Типы и основные параметры.
|
||||
|
Последнее изменение этой страницы: 2021-06-14; просмотров: 177; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.216.248 (0.008 с.) |

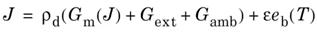
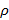 – коэффициент диффузного отражения,
– коэффициент диффузного отражения, 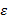 – коэффициент излучения, eb – энергетическая светимость абсолютно чёрного тела, Gm – освещенность падающего излучения с других поверхностей модели, Gext – излучение внешних источников, Gamb – окружающей среды.
– коэффициент излучения, eb – энергетическая светимость абсолютно чёрного тела, Gm – освещенность падающего излучения с других поверхностей модели, Gext – излучение внешних источников, Gamb – окружающей среды.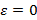 .
.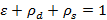 и используется уравнение для основного граничного условия с учётом этой связи.
и используется уравнение для основного граничного условия с учётом этой связи.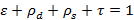 )
)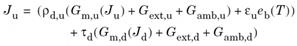
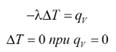
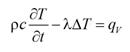
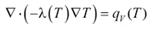
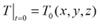
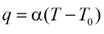
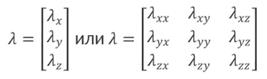
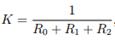
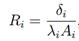
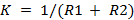 . Термические сопротивления определяются как
. Термические сопротивления определяются как