
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Коэффициент теплопроводностиСодержание книги
Поиск на нашем сайте
Коэффициент теплопроводности - тепловой поток, передаваемый через единичную поверхность при единичном значении температурного градиента:
Для каждого тела
где Значение коэффициента теплопроводности для некоторых металлов, сплавов и неметаллов приведены в таблице 1.1. Таблица 1.1 Коэффициенты теплопроводностей конструкционных материалов
Теплопроводность камня намного выше, чем у дерева, поэтому в холодную погоду лучше сидеть на деревянной поверхности, она заберет куда меньше тепла из тела человека. Оценим тепловой поток от человека к камню на котором он сидит и к бревну, при температуре окружающего воздуха (и предметов находящихся с ним в тепловом равновесии) 25 0 С, 15 0 С и 5 0 С. Плотность теплового потока:
где L – толщина стенки. Тепловой поток:
Температура человека составляет 36,6 0 С, площадь соприкосновения с поверхностью скамейки 0,05 м2, толщина скамейки 0,07 м. Таблица 1.2 Значения тепловых потоков и их плотностей
Дерево действительно заберет в несколько раз меньше тепла, чем камень. Нельзя сидеть на холодной каменной поверхности, поскольку есть риск застудить почки, а также другие органы.
Как уже было сказано выше, коэффициент теплопроводности
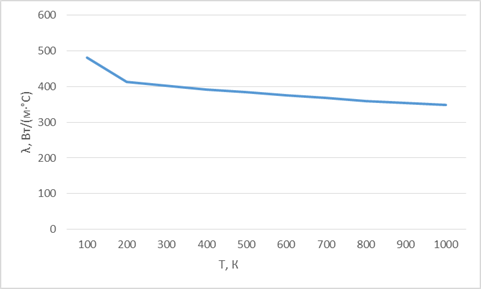
Рисунок 1.1 Зависимость коэффициента теплопроводности от температуры меди
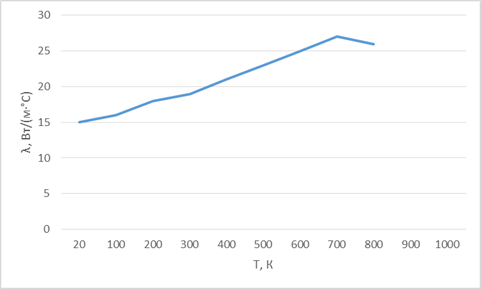
Рисунок 1.2 Зависимость коэффициента теплопроводности от температуры стали 12X18H10T
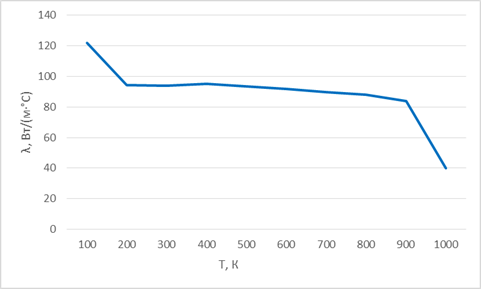
Рисунок 1.3 Зависимость коэффициента теплопроводности от температуры АМг6
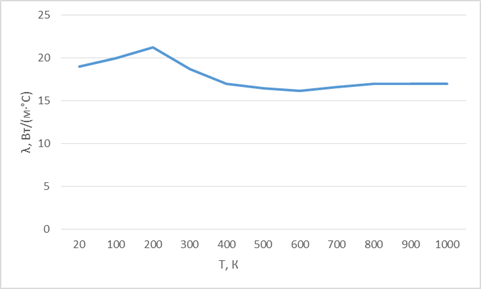
Рисунок 1.4 Зависимость коэффициента теплопроводности от температуры ВТ1- 0
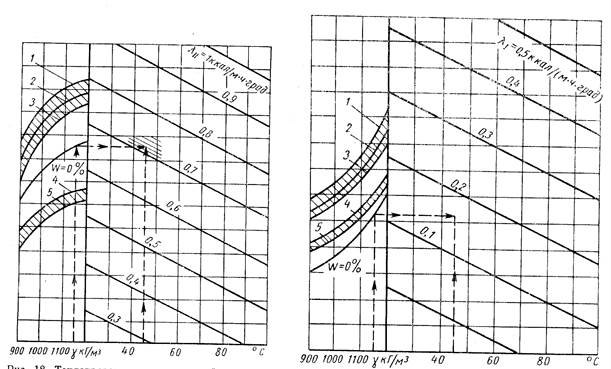
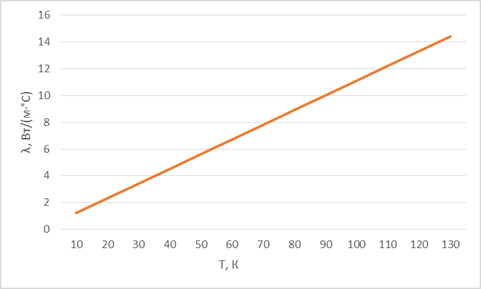
Рисунок 1.5 Теплопроводность прессованной древесины вдоль и поперек волокон в зависимости от объёмного веса и температуры.
Рисунок 1.6 Зависимость коэффициента теплопроводности от температуры для текстолита Данных по теплопроводности камня и пвх при разных температурах отсутствуют, поскольку их не используют при больших температурах либо они не важны.
Уравнение теплового баланса При расчете тепловых процессов КА обычно используется метод сосредоточенных параметров. Сущность данного метода состоит в следующем: моделируемый объект разбивается на отдельные дискретные элементы таким образом, что температуру каждого элемента в некотором приближении можно считать однородной и изменяющейся только со временем. Эти элементы называются узлами. Каждый узел состоит из одной или нескольких поверхностей с заданными коэффициентами поглощения солнечного излучения AS и степенями черноты e, описывающими их радиационные свойства. Математическая модель объекта строится как система уравнений теплового баланса для каждого узла и включает тепловые потоки к узлу от лучистого и кондуктивного теплообмена его с другими узлами, потоки от тепловыделяющего оборудования, нагревателей системы терморегулирования и от внешнего окружения (Земли и Солнца) [5]. Так как конвективный теплообмен в орбитальных условиях отсутствует, то система дифференциальных уравнений, описывающая тепловую математическую модель объекта, имеет вид
где t – время; N – число узлов; i – номер узла;
Так как основные законы лучистого теплообмена справедливы для замкнутой системы поверхностей, в математическую модель введен дополнительный нерасчетный узел «космос» с фиксированной температурой Tspace, представляющий собой сферу с абсолютно черной внутренней поверхностью, которая содержит геометрическую модель КА. В уравнении теплового баланса для КА В большинстве задач рассматривается только лучистый теплообмен между деталями, поскольку он намного больше кондуктивного. Так происходит из-за того, что в членах, отвечающих за кондуктивность количество энергии зависит от разности температур в 1 степени, а в членах, отвечающих за лучистый теплообмен – в 4. Однако, если разница температур будет близка к единице, то теплообменом теплопроводностью нельзя будет пренебречь. Базовым инструментом расчета лучистого теплообмена является безразмерный угловой коэффициент Fij, который описывает долю теплового потока, излученного с i-й поверхности площадью Si и попавшего на j-ю поверхность площадью Sj для случая абсолютно черных поверхностей. Коэффициент рассчитывается следующим образом
где rij - расстояние между элементарными площадками dSi и dSj; Задача: рассчитать угловой коэффициент для 2-х смотрящих друг на друга прямоугольных площадок размерами 1 метр на 1 метр. Температура одной поддерживается 0 0 С, другой 100 0 С. Степени черноты у обоих Решение: Поскольку углы между направлениями внешних нормалей к площадкам и отрезку, соединяющим центры элементарных площадок равны 0, то
Пусть расстояние между площадками 1 м, тогда Далее найдём тепловой поток горячей площадки
Из него на вторую пластину попадет и поглотиться
поскольку степень черноты и коэффициент поглощения поверхности – тождественные величины при одной и той же температуре этой поверхности и учитывая уравнение теплового баланса.
Соединим площадки стальной штангой. Теплопроводность штанги при 100 0 С
Видно, что кондуктивный теплообмен через штангу во много раз меньше, чем лучистый из-за степени в разнице температур, как уже отмечалось ранее. Теперь повысим температуру горячей площадки до 1000 0 С. Тогда холодной поглотиться
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-06-14; просмотров: 130; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.128.168.219 (0.008 с.) |
|||||||||||||||||||||||||||||||||||||||||||||||||

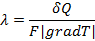
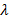 имеет свое численное значение и, зависит от природы, пористости, влажности, давления, температуры и других параметров. Численное значение определяется опытным путем (в справочных таблицах). При выводе уравнения принято, что
имеет свое численное значение и, зависит от природы, пористости, влажности, давления, температуры и других параметров. Численное значение определяется опытным путем (в справочных таблицах). При выводе уравнения принято, что 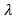 не зависит от температуры. Как показывают опыты, для многих материалов, зависимость коэффициента теплопроводности от температуры можно принять линейной во всем рассматриваемом интервале температур:
не зависит от температуры. Как показывают опыты, для многих материалов, зависимость коэффициента теплопроводности от температуры можно принять линейной во всем рассматриваемом интервале температур: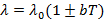
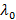 – коэффициент теплопроводности при температуре(0°C); b – постоянная, характеризующая приращение (уменьшение)
– коэффициент теплопроводности при температуре(0°C); b – постоянная, характеризующая приращение (уменьшение) 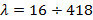 Вт/(м·°C). У большей части металлов с возрастанием температуры он уменьшается.
Вт/(м·°C). У большей части металлов с возрастанием температуры он уменьшается.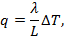
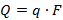

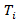 ,
, 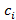 – температура и теплоемкость i-го узла; aij, bij – термические проводимости и коэффициенты лучистой термической связи между i-м и j-м узлами соответственно; Tk,non, Nnon, aik,non – температуры немоделируемых объектов, их количество и кондуктивные связи с расчетными узлами; Tspace – температура открытого космоса;
– температура и теплоемкость i-го узла; aij, bij – термические проводимости и коэффициенты лучистой термической связи между i-м и j-м узлами соответственно; Tk,non, Nnon, aik,non – температуры немоделируемых объектов, их количество и кондуктивные связи с расчетными узлами; Tspace – температура открытого космоса; 
 – внешние тепловые потоки от Земли и Солнца, поглощенные поверхностью i-го узла;
– внешние тепловые потоки от Земли и Солнца, поглощенные поверхностью i-го узла; 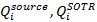 – тепловые потоки к i-му узлу от тепловыделяющего оборудования и СОТР КА.
– тепловые потоки к i-му узлу от тепловыделяющего оборудования и СОТР КА.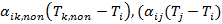 являются кондуктивными членами, остальные члены отвечают за лучистый теплообмен. Таким образом, теплообмен в КА можно назвать лучисто-кондуктивным.
являются кондуктивными членами, остальные члены отвечают за лучистый теплообмен. Таким образом, теплообмен в КА можно назвать лучисто-кондуктивным.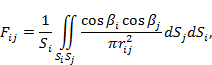
 и
и 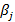 – углы между направлениями внешних нормалей к площадкам и отрезку rij, соединяющим центры элементарных площадок.
– углы между направлениями внешних нормалей к площадкам и отрезку rij, соединяющим центры элементарных площадок.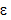 = 0.9. Посчитать поток излучением от более горячей к более холодной. Соединить их стальной 12X18H10T штангой (стержнем) диаметром 5 см. Коэффициент теплопроводности взять средний для температур 0 0 С и 100 0 С. Далее увеличить температуру второй площадки до 1000 0 С, снова пересчитать оба значения.
= 0.9. Посчитать поток излучением от более горячей к более холодной. Соединить их стальной 12X18H10T штангой (стержнем) диаметром 5 см. Коэффициент теплопроводности взять средний для температур 0 0 С и 100 0 С. Далее увеличить температуру второй площадки до 1000 0 С, снова пересчитать оба значения.
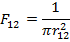
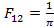
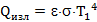
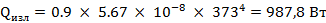
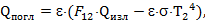
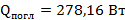
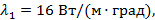 при 0 0 С
при 0 0 С 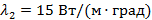 . Оценим тепловой поток через штангу:
. Оценим тепловой поток через штангу: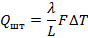
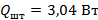
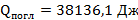 за счет лучистого теплообмена и
за счет лучистого теплообмена и 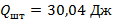 через штангу.
через штангу.


