
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Решение некоторых типовых задач, рассматриваемых в аудиторииСодержание книги
Поиск на нашем сайте 14.4.1. Вычислите интеграл Решение. Вычислим дифференциал длины дуги 14.4.2. Вычислить с помощью криволинейного интеграла площадь части цилиндрической поверхности
Решение. Если направляющей цилиндрической поверхности является кривая В нашем примере для вычисления интеграла удобно задать кривую Тогда
14.4.3. Вычислить криволинейный интеграл Решение. Вычислим дифференциал длины дуги винтовой линии:
14.4.4. Вычислить интеграл Решение. Первая поверхность — сфера радиуса
14.4.5. Вычислить криволинейный интеграл
Решение. Уравнение лемнискаты удобнее записать в полярных координатах:
14.4.6. Вычислить интеграл Решение. а) б) в) Здесь удобнее перейти к интегрированию по переменной
Очевидно, криволинейный интеграл между двумя точками зависит от дуги, соединяющей эти точки. 14.4.7. Найти криволинейный интеграл второго рода Решение. Зададим линию параметрически. Именно, пусть Вычислим дифференциалы переменных: 14.4.8. Найти работу силы Решение. Зададим контур параметрически:
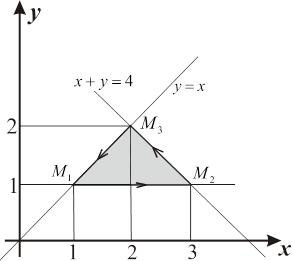
14.4.9. Вычислить интеграл Решение. Преобразуем криволинейный интеграл второго рода по замкнутому контуру в двойной по формуле Грина (см. пункт 14.3). Найдем Тогда
Здесь контур треугольника обходится против часовой стрелки, как показано на рис. 14.4, а область 14.4.10. Проверить, что выражение Решение. Найдем функцию На отрезке
Задачи для самостоятельного решения ДИСТАНЦИОННОЕ ОБУЧЕНИЕ (ЧАСТЬ Б) 14.5.1. Вычислить криволинейные интегралы: а) 14.5.2. Найти координаты центра масс винтовой линии 14.5.3. Вычислить площадь части цилиндрической поверхности 14.5.4. Вычислить криволинейный интеграл 14.5.5. Вычислить: а) 14.5.6. Вычислить интеграл 14.5.7. Проверить, что выражение
Ответы. 14.5.1. а)
ЧАСТЬ В)
|
||||||
|
Последнее изменение этой страницы: 2021-06-14; просмотров: 180; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.137 (0.006 с.) |

 по дуге параболы
по дуге параболы 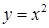 между точками
между точками  и
и  .
. . Здесь
. Здесь 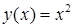 , поэтому
, поэтому 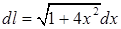 . Криволинейный интеграл сводится к определенному интегралу:
. Криволинейный интеграл сводится к определенному интегралу: 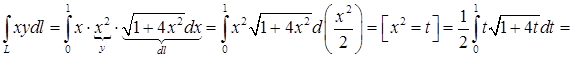
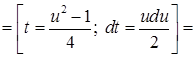
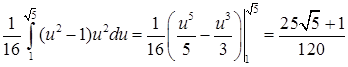 .
.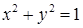
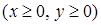 , ограниченной снизу плоскостью
, ограниченной снизу плоскостью 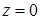 , а сверху поверхностью
, а сверху поверхностью 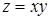 .
.
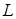 , лежащая в плоскости
, лежащая в плоскости 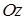 , причем для каждой образующей
, причем для каждой образующей 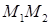 точка
точка 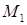 лежит на кривой
лежит на кривой 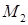 – на поверхности
– на поверхности 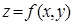 , ограничивающей цилиндрическую поверхность сверху (рис. 14.3), то площадь участка цилиндрической поверхности можно вычислить с помощью криволинейного интеграла:
, ограничивающей цилиндрическую поверхность сверху (рис. 14.3), то площадь участка цилиндрической поверхности можно вычислить с помощью криволинейного интеграла: 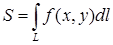 . В этом заключается геометрический смысл криволинейного интеграла первого рода.
. В этом заключается геометрический смысл криволинейного интеграла первого рода.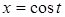 ,
, 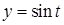
 . Дифференциал длины дуги равен
. Дифференциал длины дуги равен  .
. .
. , где
, где  ,
, 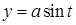 ,
, 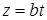 .
.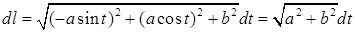 . Подынтегральная функция на кривой равна
. Подынтегральная функция на кривой равна  . Первому витку винтовой линии отвечает изменение параметра от
. Первому витку винтовой линии отвечает изменение параметра от  до
до 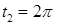 , тогда
, тогда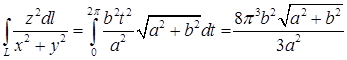 .
.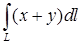 по части линии пересечения поверхностей
по части линии пересечения поверхностей  ,
,  , лежащей в первом октанте.
, лежащей в первом октанте. с центром в начале координат, вторая — плоскость, проходящая через центр сферы. Пересечением этих поверхностей является окружность. Зададим ее параметрически. Подставив
с центром в начале координат, вторая — плоскость, проходящая через центр сферы. Пересечением этих поверхностей является окружность. Зададим ее параметрически. Подставив  в уравнение сферы, получим
в уравнение сферы, получим 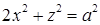 . Этому уравнению тождественно удовлетворяет подстановка
. Этому уравнению тождественно удовлетворяет подстановка  ,
, 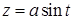 . Следовательно, параметрическими уравнениями линии
. Следовательно, параметрическими уравнениями линии  ,
,  . Вычислим дифференциал длины дуги
. Вычислим дифференциал длины дуги 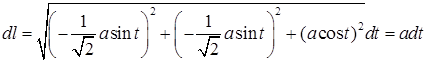 . Отсюда
. Отсюда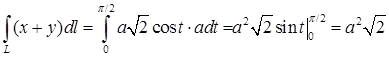 .
.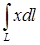 , где
, где 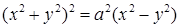 .
.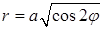 . Для правого лепестка
. Для правого лепестка 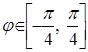 . Для лемнискаты
. Для лемнискаты  . Тогда искомый интеграл запишем в виде:
. Тогда искомый интеграл запишем в виде: .
. вдоль линий: а)
вдоль линий: а) 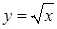 .
. .
.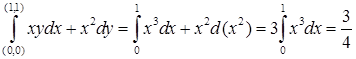 .
.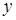 , тогда
, тогда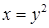 ,
, 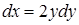 ,
, 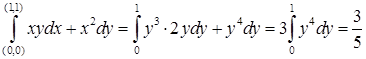 .
.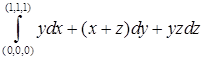 вдоль линии пересечения поверхностей
вдоль линии пересечения поверхностей  , тогда
, тогда 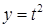 и
и 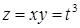 . Параметр
. Параметр 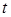 при этом изменяется от
при этом изменяется от 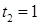 .
.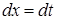 ,
, 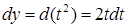 ,
, 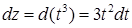 . Криволинейный интеграл равен
. Криволинейный интеграл равен 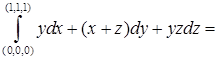
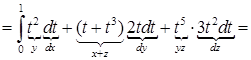
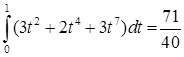 .
.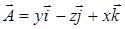 вдоль кривой
вдоль кривой  ориентированной против часовой стрелки со стороны оси
ориентированной против часовой стрелки со стороны оси 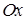 .
. ,
, 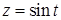 . Легко проверить, что уравнения системы при этом превращаются в тождественные равенства. Обходу контура против часовой стрелки, если смотреть со стороны оси абсцисс, отвечает изменение параметра от
. Легко проверить, что уравнения системы при этом превращаются в тождественные равенства. Обходу контура против часовой стрелки, если смотреть со стороны оси абсцисс, отвечает изменение параметра от 
 .
. , если
, если 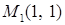 ,
,  ,
, 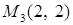 .
.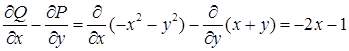 .
.

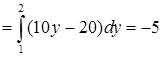 .
.
 — треугольник
— треугольник  . Непосредственное вычисление криволинейного интеграла
. Непосредственное вычисление криволинейного интеграла  является полным дифференциалом некоторой функции
является полным дифференциалом некоторой функции 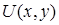 , и найти эту функцию.
, и найти эту функцию.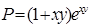 ,
, 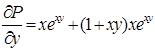 ;
; 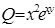 ,
, 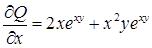 . Очевидно, что
. Очевидно, что 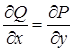 , т. е. условие полного дифференциала выполнено.
, т. е. условие полного дифференциала выполнено.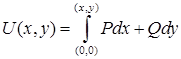 , при этом воспользуемся независимостью криволинейного интеграла от пути интегрирования и соединим точки
, при этом воспользуемся независимостью криволинейного интеграла от пути интегрирования и соединим точки  ломаной линией, состоящей из двух звеньев:
ломаной линией, состоящей из двух звеньев: 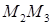 , соединяющих точки
, соединяющих точки  ,
, 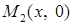 и
и 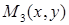 . Итак,
. Итак,  .
.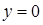 и
и 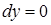 , отсюда
, отсюда  . На отрезке
. На отрезке 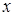 не меняется (
не меняется ( ), а ордината изменяется от
), а ордината изменяется от  до
до 
 . Складывая вычисленные интегралы, получим
. Складывая вычисленные интегралы, получим  . Учитывая, что в качестве начальной точки можно было выбрать не
. Учитывая, что в качестве начальной точки можно было выбрать не 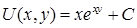 , где
, где  – произвольная постоянная.
– произвольная постоянная. 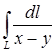 , где
, где 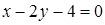 , заключенный между точками
, заключенный между точками 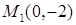 и
и 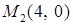 ; б)
; б) 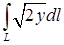 , где
, где 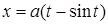 ,
, 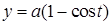 ; в)
; в) 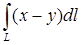 , где
, где 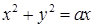 ; г)
; г) 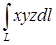 , где
, где 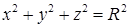 ,
, 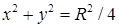 , лежащая в первом октанте.
, лежащая в первом октанте. ,
, 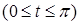 , считая линию однородной.
, считая линию однородной.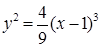 , заключенной между плоскостью
, заключенной между плоскостью 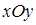 и поверхностью
и поверхностью 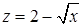 (
(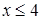 ).
).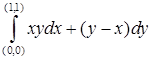 вдоль линии: а)
вдоль линии: а) 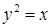 ; г)
; г) 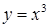 .
.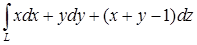 , где
, где 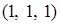 до точки
до точки 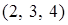 ; б)
; б) 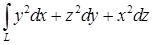 , где
, где 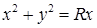 (
(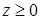 ). Направление обхода линии против часовой стрелки при взгляде из начала координат.
). Направление обхода линии против часовой стрелки при взгляде из начала координат.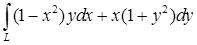 по окружности
по окружности 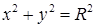 непосредственно и с помощью формулы Грина.
непосредственно и с помощью формулы Грина.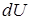 является полным дифференциалом некоторой функции
является полным дифференциалом некоторой функции 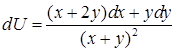 ; б)
; б) 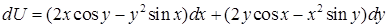 .
. ; б)
; б) 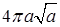 ; в)
; в) 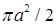 ; г)
; г) 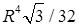 . 14.5.2.
. 14.5.2. 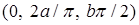 . 14.5.3.
. 14.5.3. 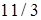 . 14.5.4. а)
. 14.5.4. а) 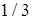 ; б)
; б) 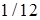 ; в)
; в) 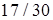 ; г)
; г) 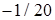 . 14.5.5. а)
. 14.5.5. а) 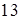 ; б)
; б) 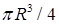 . 14.5.6.
. 14.5.6. 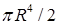 . 14.5.7. а)
. 14.5.7. а) 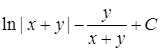 ; б)
; б) 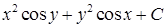 .
.


