Поверхностные интегралы второго рода
ЗАНЯТИЕ №7
ДИСТАНЦИОННОЕ ОБУЧЕНИЕ
ЧАСТЬ А)
ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ ВТОРОГО РОДА
Поверхностные интегралы второго рода
Поверхностный интеграл второго рода можно определить, опираясь на понятие поверхностного интеграла первого рода (см. пункт 12.2). Пусть в каждой точке 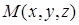 поверхности поверхности 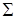 задано векторное поле задано векторное поле 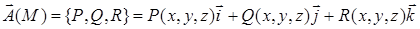 . Очевидно, чтобы задать векторное поле, достаточно указать три его компоненты — скалярные функции . Очевидно, чтобы задать векторное поле, достаточно указать три его компоненты — скалярные функции 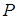 , , 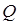 , , 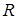 от трех переменных от трех переменных 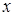 , , 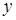 и и 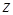 . В каждой точке поверхности . В каждой точке поверхности 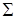 выберем единичную нормаль выберем единичную нормаль 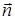 (рис. 12.1) так, чтобы она менялась непрерывным образом. Это можно сделать одним из двух способов: выбрать (рис. 12.1) так, чтобы она менялась непрерывным образом. Это можно сделать одним из двух способов: выбрать 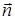 или или 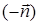 . Говорят, что при этом выбрана определенная сторона поверхности. Скалярное произведение . Говорят, что при этом выбрана определенная сторона поверхности. Скалярное произведение 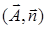 , проинтегрированное по поверхности , проинтегрированное по поверхности 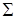 в смысле интеграла первого рода, как раз и дает поверхностный интеграл второго рода, который иначе называют потоком векторного поля в смысле интеграла первого рода, как раз и дает поверхностный интеграл второго рода, который иначе называют потоком векторного поля 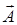 : : 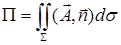 . Учитывая координаты единичного вектора . Учитывая координаты единичного вектора 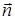 , запишем подынтегральное выражение так: , запишем подынтегральное выражение так:
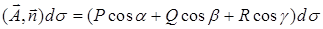 , но , но 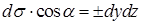 , ,
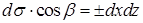 , , 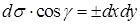 (ср. пункт 12.1), отсюда координатная запись потока вектора принимает вид (ср. пункт 12.1), отсюда координатная запись потока вектора принимает вид
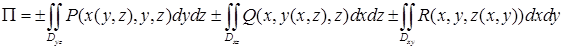 . .
В последней формуле перед каждым двойным интегралом выбирается знак, совпадающий со знаком 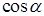 , , 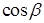 или или 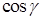 соответственно (т. е. плюс, если вектор соответственно (т. е. плюс, если вектор 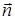 составляет острый угол с соответствующей координатной осью, и минус, если этот угол тупой). Обратите внимание, что в каждом из интегралов подынтегральная функция выражена через переменные интегрирования, т. е. третья переменная исключена согласно уравнению, задающему поверхность составляет острый угол с соответствующей координатной осью, и минус, если этот угол тупой). Обратите внимание, что в каждом из интегралов подынтегральная функция выражена через переменные интегрирования, т. е. третья переменная исключена согласно уравнению, задающему поверхность  . Такой метод сведения поверхностного интеграла второго рода к трем двойным (т. н. метод проектирования на три координатные плоскости) удобен только в случае, когда поверхность . Такой метод сведения поверхностного интеграла второго рода к трем двойным (т. н. метод проектирования на три координатные плоскости) удобен только в случае, когда поверхность 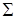 взаимно-однозначно проектируется на каждую из трех координатных плоскостей (в взаимно-однозначно проектируется на каждую из трех координатных плоскостей (в 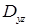 , , 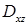 , , 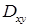 ), иначе ), иначе 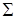 необходимо разбить на несколько частей, что приводит к значительному увеличению объема вычислений. Поэтому мы рекомендуем метод проектирования на одну координатную плоскость. Пусть, для определенности, это будет плоскость необходимо разбить на несколько частей, что приводит к значительному увеличению объема вычислений. Поэтому мы рекомендуем метод проектирования на одну координатную плоскость. Пусть, для определенности, это будет плоскость 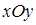 , а нормаль , а нормаль 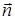 составляет острый угол с осью составляет острый угол с осью 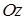 . Тогда подынтегральное выражение в поверхностном интеграле второго рода равно . Тогда подынтегральное выражение в поверхностном интеграле второго рода равно
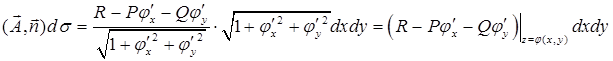 . .
Итак, поток векторного поля сводится к двойному интегралу по формуле
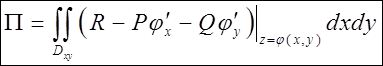 . .
Все обозначения в этой формуле соответствуют рисунку 12.1. Переменная 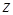 в функциях в функциях 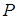 , , 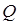 , , 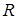 заменяется на заменяется на 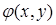 из уравнения поверхности из уравнения поверхности 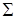 . .
В заключение заметим, что векторная запись потока 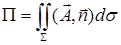 эквивалентна записи эквивалентна записи 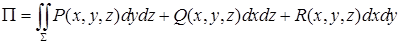 в координатной форме, где в координатной форме, где 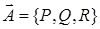 . .
ДИСТАНЦИОННОЕ ОБУЧЕНИЕ (ЧАСТЬ А)
13.3.1. Вычислить 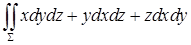 , где , где 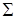 – внешняя сторона куба – внешняя сторона куба 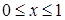 , , 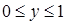 , , 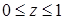 . .
13.3.2. Вычислить 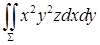 , где , где 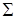 – внешняя сторона нижней половины сферы – внешняя сторона нижней половины сферы 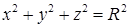 . .
13.3.3. Вычислить 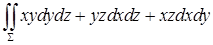 , где , где 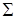 – внешняя сторона пирамиды, составленной плоскостями – внешняя сторона пирамиды, составленной плоскостями 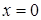 , , 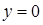 , , 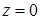 и и 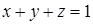 . .
13.3.4. Вычислить 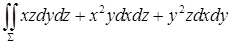 , где , где 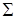 – внешняя сторона поверхности, расположенной в первом октанте и составленной из параболоида вращения – внешняя сторона поверхности, расположенной в первом октанте и составленной из параболоида вращения 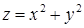 , цилиндра , цилиндра 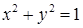 и координатных плоскостей. и координатных плоскостей.
13.3.5. Вычислить поток радиус-вектора через боковую поверхность кругового конуса, основание которого находится на плоскости 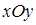 , а ось совпадает с осью , а ось совпадает с осью 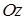 . Высота конуса равна 1, радиус основания равен 2. . Высота конуса равна 1, радиус основания равен 2.
13.3.6. Найти поток вектора 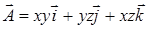 через внешнюю сторону части сферы через внешнюю сторону части сферы 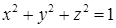 , заключенной в первом октанте. , заключенной в первом октанте.
Ответы. 13.3.1. 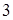 . 13.3.2. . 13.3.2. 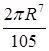 . 13.3.3. . 13.3.3. 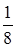 . 13.3.4. . 13.3.4. 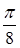 . 13.3.5. . 13.3.5. 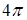 . 13.3.6. . 13.3.6. 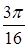 . .
ЧАСТЬ Б)
КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
Формула Грина
Пусть 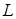 — замкнутый контур, расположенный в плоскости — замкнутый контур, расположенный в плоскости 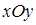 . Криволинейный интеграл второго рода . Криволинейный интеграл второго рода 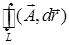 можно свести к двойному по формуле Грина: можно свести к двойному по формуле Грина:
 . .
Здесь 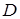 – область, ограниченная контуром – область, ограниченная контуром 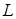 , который обходится в положительном направлении, т. е. против часовой стрелки. При изменении направления обхода контура интеграл , который обходится в положительном направлении, т. е. против часовой стрелки. При изменении направления обхода контура интеграл 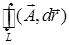 меняет знак. меняет знак.
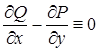 — условие независимости интеграла — условие независимости интеграла 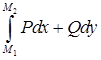 от пути, соединяющего точки от пути, соединяющего точки 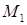 и и 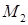 . При этом выражение . При этом выражение 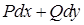 является полным дифференциалом некоторой функции двух переменных является полным дифференциалом некоторой функции двух переменных 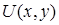 , а сама функция может быть найдена по формуле , а сама функция может быть найдена по формуле 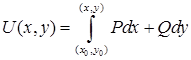 , где , где 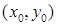 — произвольная точка, в которой функции — произвольная точка, в которой функции 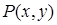 и и 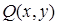 определены. определены.
ДИСТАНЦИОННОЕ ОБУЧЕНИЕ (ЧАСТЬ Б)
14.5.1. Вычислить криволинейные интегралы: а) 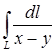 , где , где 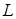 – отрезок прямой – отрезок прямой 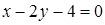 , заключенный между точками , заключенный между точками 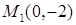 и и 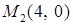 ; б) ; б) 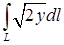 , где , где 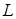 – первая арка циклоиды – первая арка циклоиды 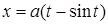 , , 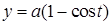 ; в) ; в) 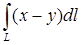 , где , где 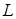 – окружность – окружность 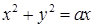 ; г) ; г) 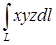 , где , где 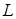 – четверть окружности – четверть окружности 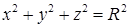 , , 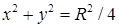 , лежащая в первом октанте. , лежащая в первом октанте.
14.5.2. Найти координаты центра масс винтовой линии  , , 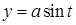 , , 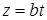 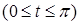 , считая линию однородной. , считая линию однородной.
14.5.3. Вычислить площадь части цилиндрической поверхности 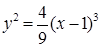 , заключенной между плоскостью , заключенной между плоскостью 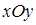 и поверхностью и поверхностью 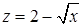 ( (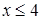 ). ).
14.5.4. Вычислить криволинейный интеграл 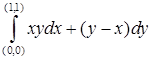 вдоль линии: а) вдоль линии: а) 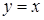 ; б) ; б) 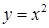 ; в) ; в) 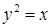 ; г) ; г) 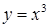 . .
14.5.5. Вычислить: а) 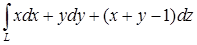 , где , где 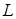 – отрезок прямой от точки – отрезок прямой от точки 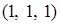 до точки до точки 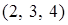 ; б) ; б) 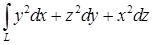 , где , где 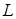 – линия пересечения сферы – линия пересечения сферы 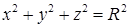 и цилиндра и цилиндра 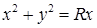 ( (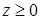 ). Направление обхода линии против часовой стрелки при взгляде из начала координат. ). Направление обхода линии против часовой стрелки при взгляде из начала координат.
14.5.6. Вычислить интеграл 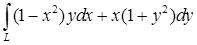 по окружности по окружности 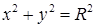 непосредственно и с помощью формулы Грина. непосредственно и с помощью формулы Грина.
14.5.7. Проверить, что выражение 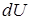 является полным дифференциалом некоторой функции является полным дифференциалом некоторой функции 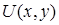 , и найти эту функцию, если: а) , и найти эту функцию, если: а) 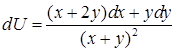 ; б) ; б) 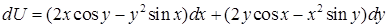 . .
Ответы. 14.5.1. а)  ; б) ; б) 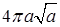 ; в) ; в) 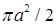 ; г) ; г) 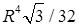 . 14.5.2. . 14.5.2. 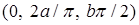 . 14.5.3. . 14.5.3. 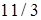 . 14.5.4. а) . 14.5.4. а) 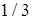 ; б) ; б) 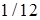 ; в) ; в) 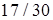 ; г) ; г) 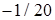 . 14.5.5. а) . 14.5.5. а) 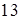 ; б) ; б) 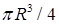 . 14.5.6. . 14.5.6. 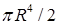 . 14.5.7. а) . 14.5.7. а) 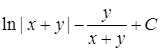 ; б) ; б) 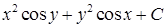 . .
ЧАСТЬ В)
ДИСТАЦИОННОЕ ОБУЧЕНИЕ (ЧАСТЬ В)
15.4.1. Найти 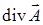 , если: а) , если: а) 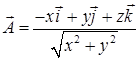 ; б) ; б) 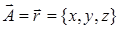 . .
15.4.2. Решить задачи 13.3.1, 13.3.3, 13.3.4, 13.3.5 с помощью формулы Гаусса.
15.4.3. Вычислить поток векторного поля 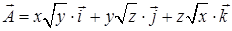 через внешнюю сторону границы области, ограниченной поверхностями через внешнюю сторону границы области, ограниченной поверхностями 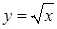 , , 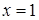 , , 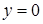 , , 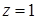 и и 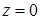 . .
15.4.4. Вычислить поток векторного поля 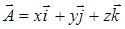 через внешнюю сторону границы области, ограниченной поверхностями через внешнюю сторону границы области, ограниченной поверхностями 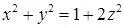 , , 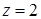 и и 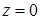 . .
Ответы. 15.4.1. а) 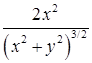 ; б) ; б) 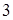 . 15.4.3. . 15.4.3. 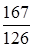 . 15.4.4. . 15.4.4. 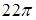 . .
ЗАНЯТИЕ №7
ДИСТАНЦИОННОЕ ОБУЧЕНИЕ
ЧАСТЬ А)
ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ ВТОРОГО РОДА
Поверхностные интегралы второго рода
Поверхностный интеграл второго рода можно определить, опираясь на понятие поверхностного интеграла первого рода (см. пункт 12.2). Пусть в каждой точке 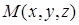 поверхности поверхности 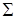 задано векторное поле задано векторное поле 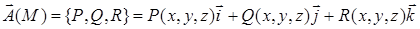 . Очевидно, чтобы задать векторное поле, достаточно указать три его компоненты — скалярные функции . Очевидно, чтобы задать векторное поле, достаточно указать три его компоненты — скалярные функции 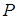 , , 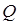 , , 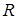 от трех переменных от трех переменных 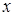 , , 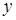 и и 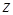 . В каждой точке поверхности . В каждой точке поверхности 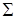 выберем единичную нормаль выберем единичную нормаль 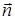 (рис. 12.1) так, чтобы она менялась непрерывным образом. Это можно сделать одним из двух способов: выбрать (рис. 12.1) так, чтобы она менялась непрерывным образом. Это можно сделать одним из двух способов: выбрать 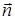 или или 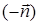 . Говорят, что при этом выбрана определенная сторона поверхности. Скалярное произведение . Говорят, что при этом выбрана определенная сторона поверхности. Скалярное произведение 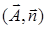 , проинтегрированное по поверхности , проинтегрированное по поверхности 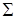 в смысле интеграла первого рода, как раз и дает поверхностный интеграл второго рода, который иначе называют потоком векторного поля в смысле интеграла первого рода, как раз и дает поверхностный интеграл второго рода, который иначе называют потоком векторного поля 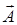 : : 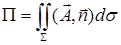 . Учитывая координаты единичного вектора . Учитывая координаты единичного вектора 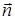 , запишем подынтегральное выражение так: , запишем подынтегральное выражение так:
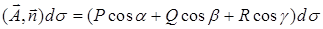 , но , но 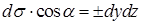 , ,
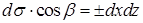 , , 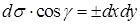 (ср. пункт 12.1), отсюда координатная запись потока вектора принимает вид (ср. пункт 12.1), отсюда координатная запись потока вектора принимает вид
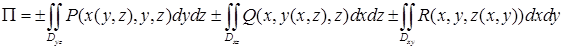 . .
В последней формуле перед каждым двойным интегралом выбирается знак, совпадающий со знаком 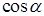 , , 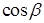 или или 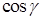 соответственно (т. е. плюс, если вектор соответственно (т. е. плюс, если вектор 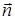 составляет острый угол с соответствующей координатной осью, и минус, если этот угол тупой). Обратите внимание, что в каждом из интегралов подынтегральная функция выражена через переменные интегрирования, т. е. третья переменная исключена согласно уравнению, задающему поверхность составляет острый угол с соответствующей координатной осью, и минус, если этот угол тупой). Обратите внимание, что в каждом из интегралов подынтегральная функция выражена через переменные интегрирования, т. е. третья переменная исключена согласно уравнению, задающему поверхность 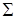 . Такой метод сведения поверхностного интеграла второго рода к трем двойным (т. н. метод проектирования на три координатные плоскости) удобен только в случае, когда поверхность . Такой метод сведения поверхностного интеграла второго рода к трем двойным (т. н. метод проектирования на три координатные плоскости) удобен только в случае, когда поверхность 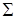 взаимно-однозначно проектируется на каждую из трех координатных плоскостей (в взаимно-однозначно проектируется на каждую из трех координатных плоскостей (в 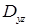 , , 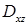 , , 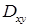 ), иначе ), иначе 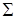 необходимо разбить на несколько частей, что приводит к значительному увеличению объема вычислений. Поэтому мы рекомендуем метод проектирования на одну координатную плоскость. Пусть, для определенности, это будет плоскость необходимо разбить на несколько частей, что приводит к значительному увеличению объема вычислений. Поэтому мы рекомендуем метод проектирования на одну координатную плоскость. Пусть, для определенности, это будет плоскость 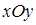 , а нормаль , а нормаль 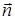 составляет острый угол с осью составляет острый угол с осью  . Тогда подынтегральное выражение в поверхностном интеграле второго рода равно . Тогда подынтегральное выражение в поверхностном интеграле второго рода равно
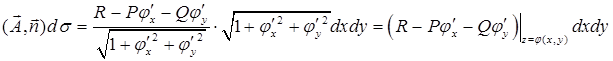 . .
Итак, поток векторного поля сводится к двойному интегралу по формуле
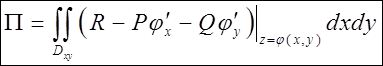 . .
Все обозначения в этой формуле соответствуют рисунку 12.1. Переменная  в функциях в функциях 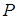 , , 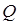 , , 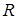 заменяется на заменяется на 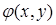 из уравнения поверхности из уравнения поверхности 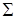 . .
В заключение заметим, что векторная запись потока 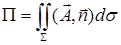 эквивалентна записи эквивалентна записи 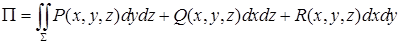 в координатной форме, где в координатной форме, где 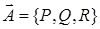 . .
|



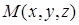 поверхности
поверхности 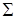 задано векторное поле
задано векторное поле 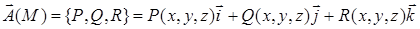 . Очевидно, чтобы задать векторное поле, достаточно указать три его компоненты — скалярные функции
. Очевидно, чтобы задать векторное поле, достаточно указать три его компоненты — скалярные функции 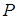 ,
, 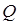 ,
, 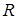 от трех переменных
от трех переменных 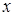 ,
, 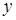 и
и 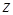 . В каждой точке поверхности
. В каждой точке поверхности 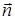 (рис. 12.1) так, чтобы она менялась непрерывным образом. Это можно сделать одним из двух способов: выбрать
(рис. 12.1) так, чтобы она менялась непрерывным образом. Это можно сделать одним из двух способов: выбрать 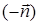 . Говорят, что при этом выбрана определенная сторона поверхности. Скалярное произведение
. Говорят, что при этом выбрана определенная сторона поверхности. Скалярное произведение 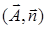 , проинтегрированное по поверхности
, проинтегрированное по поверхности 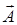 :
: 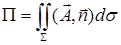 . Учитывая координаты единичного вектора
. Учитывая координаты единичного вектора 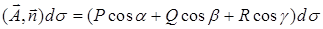 , но
, но 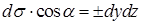 ,
,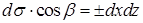 ,
, 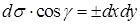 (ср. пункт 12.1), отсюда координатная запись потока вектора принимает вид
(ср. пункт 12.1), отсюда координатная запись потока вектора принимает вид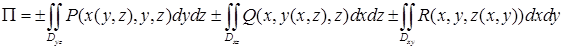 .
.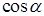 ,
, 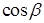 или
или 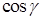 соответственно (т. е. плюс, если вектор
соответственно (т. е. плюс, если вектор 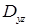 ,
, 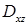 ,
, 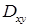 ), иначе
), иначе 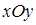 , а нормаль
, а нормаль 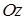 . Тогда подынтегральное выражение в поверхностном интеграле второго рода равно
. Тогда подынтегральное выражение в поверхностном интеграле второго рода равно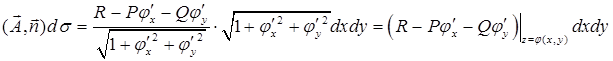 .
.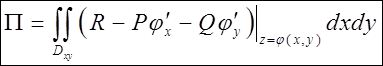 .
.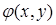 из уравнения поверхности
из уравнения поверхности 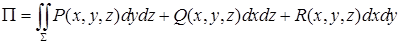 в координатной форме, где
в координатной форме, где 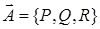 .
.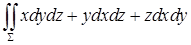 , где
, где 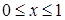 ,
, 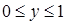 ,
, 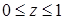 .
.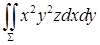 , где
, где 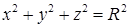 .
.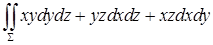 , где
, где 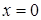 ,
, 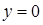 ,
, 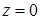 и
и 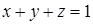 .
.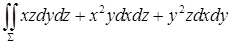 , где
, где 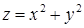 , цилиндра
, цилиндра 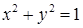 и координатных плоскостей.
и координатных плоскостей.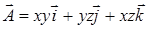 через внешнюю сторону части сферы
через внешнюю сторону части сферы 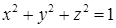 , заключенной в первом октанте.
, заключенной в первом октанте.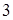 . 13.3.2.
. 13.3.2. 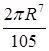 . 13.3.3.
. 13.3.3. 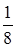 . 13.3.4.
. 13.3.4. 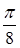 . 13.3.5.
. 13.3.5. 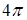 . 13.3.6.
. 13.3.6. 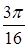 .
.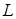 — замкнутый контур, расположенный в плоскости
— замкнутый контур, расположенный в плоскости 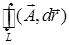 можно свести к двойному по формуле Грина:
можно свести к двойному по формуле Грина: .
.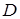 – область, ограниченная контуром
– область, ограниченная контуром 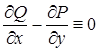 — условие независимости интеграла
— условие независимости интеграла 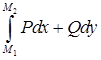 от пути, соединяющего точки
от пути, соединяющего точки 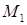 и
и 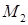 . При этом выражение
. При этом выражение 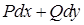 является полным дифференциалом некоторой функции двух переменных
является полным дифференциалом некоторой функции двух переменных 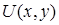 , а сама функция может быть найдена по формуле
, а сама функция может быть найдена по формуле 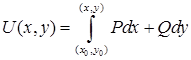 , где
, где 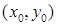 — произвольная точка, в которой функции
— произвольная точка, в которой функции 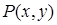 и
и 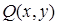 определены.
определены.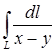 , где
, где 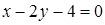 , заключенный между точками
, заключенный между точками 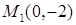 и
и 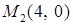 ; б)
; б) 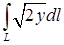 , где
, где 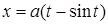 ,
, 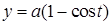 ; в)
; в) 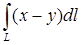 , где
, где 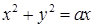 ; г)
; г) 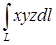 , где
, где 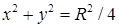 , лежащая в первом октанте.
, лежащая в первом октанте. ,
, 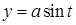 ,
, 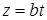
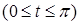 , считая линию однородной.
, считая линию однородной.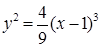 , заключенной между плоскостью
, заключенной между плоскостью 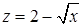 (
(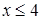 ).
).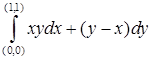 вдоль линии: а)
вдоль линии: а) 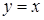 ; б)
; б) 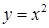 ; в)
; в) 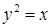 ; г)
; г) 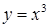 .
.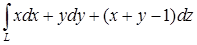 , где
, где 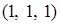 до точки
до точки 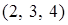 ; б)
; б) 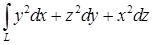 , где
, где 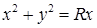 (
(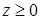 ). Направление обхода линии против часовой стрелки при взгляде из начала координат.
). Направление обхода линии против часовой стрелки при взгляде из начала координат.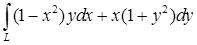 по окружности
по окружности 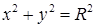 непосредственно и с помощью формулы Грина.
непосредственно и с помощью формулы Грина.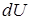 является полным дифференциалом некоторой функции
является полным дифференциалом некоторой функции 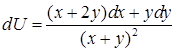 ; б)
; б) 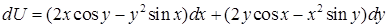 .
. ; б)
; б) 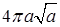 ; в)
; в) 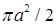 ; г)
; г) 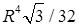 . 14.5.2.
. 14.5.2. 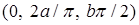 . 14.5.3.
. 14.5.3. 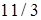 . 14.5.4. а)
. 14.5.4. а) 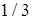 ; б)
; б) 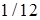 ; в)
; в) 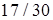 ; г)
; г) 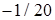 . 14.5.5. а)
. 14.5.5. а) 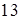 ; б)
; б) 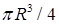 . 14.5.6.
. 14.5.6. 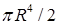 . 14.5.7. а)
. 14.5.7. а) 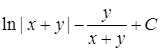 ; б)
; б) 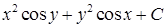 .
.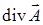 , если: а)
, если: а) 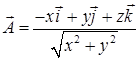 ; б)
; б) 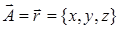 .
.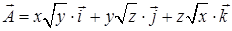 через внешнюю сторону границы области, ограниченной поверхностями
через внешнюю сторону границы области, ограниченной поверхностями 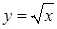 ,
, 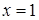 ,
, 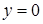 ,
, 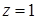 и
и 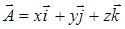 через внешнюю сторону границы области, ограниченной поверхностями
через внешнюю сторону границы области, ограниченной поверхностями 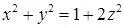 ,
, 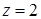 и
и 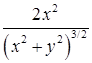 ; б)
; б) 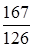 . 15.4.4.
. 15.4.4. 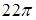 .
.


