
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Решение некоторых типовых задач, рассматриваемых в аудитории ⇐ ПредыдущаяСтр 5 из 5
12.3.1. Вычислить площадь той части поверхности Решение. Найдем элемент площади поверхности: 12.3.2. Вычислить площадь части параболоида Решение. Поверхность задана уравнением 12.3.3. Вычислить часть поверхности конуса Решение. В этом примере надо найти часть поверхности конуса, лежащую над кругом
12.3.4. Вычислить площадь части земной поверхности, считая ее сферой радиуса Решение. Используя приведенную в пункте 12.1 формулу элемента площади в сферических координатах для сферы с уравнением
12.3.5. Вычислить интеграл Решение. И боковая поверхность конуса, и его основание имеют одну и ту же проекцию на плоскость
12.3.6. Вычислить интеграл Решение. Поверхность тетраэдра состоит из четырех граней, интеграл по каждой из которых будем вычислять отдельно. Грань, лежащая в плоскости Оставшиеся три грани расположены в координатных плоскостях. Для грани, расположенной в плоскости Найдем, например
12.3.7. Вычислить Решение. Из уравнения плоскости удобнее выразить 12.3.8. Найти координаты центра масс восьмой части однородной сферы Решение. Очевидно, в силу симметричности координаты
Здесь было учтено, что проекция
12.4. Задачи для самостоятельного решения ЧАСТЬ В) ДИСТАНЦИОННОЕ ОБУЧЕНИЕ 12.4.1. Найти площадь: а) части поверхности 12.4.2. Найти центр масс части однородного параболоида 12.4.3. Вычислить поверхностный интеграл 12.4.4. Вычислить 12.4.5. Вычислить 12.4.6. Вычислить 12.4.7. Вычислить 12.4.8. Найти массу сферы, если поверхностная плотность в каждой точке равна квадрату расстояния от этой точки до некоторого фиксированного диаметра сферы.
Ответы. 12.4.1. а)
|
|||||
|
Последнее изменение этой страницы: 2021-06-14; просмотров: 701; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.84.29 (0.016 с.) |
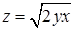 , которая находится над прямоугольником, лежащим в плоскости
, которая находится над прямоугольником, лежащим в плоскости  и ограниченным прямыми
и ограниченным прямыми  ,
, 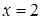 ,
, 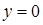 ,
, 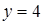 .
.
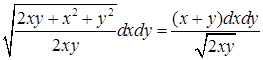 . Теперь легко найдем искомую площадь:
. Теперь легко найдем искомую площадь: 
 .
.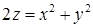 , вырезанной цилиндром
, вырезанной цилиндром 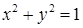 .
.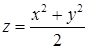 , отсюда
, отсюда 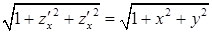 . Двойной интеграл, выражающий площадь, равен
. Двойной интеграл, выражающий площадь, равен 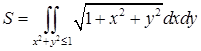 . Для его вычисления перейдем к полярным координатам:
. Для его вычисления перейдем к полярным координатам: 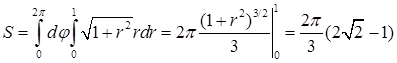 .
.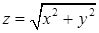 , отсекаемую цилиндром
, отсекаемую цилиндром  .
.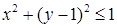 радиуса
радиуса  . Площадь круга равна
. Площадь круга равна  . Вычислим элемент поверхности конуса:
. Вычислим элемент поверхности конуса: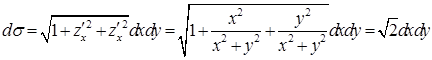 ,
, 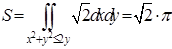 .
.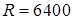 км, заключенной между меридианами
км, заключенной между меридианами 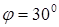 ,
, 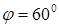 и параллелями
и параллелями 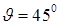 и
и 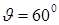 .
. , получим
, получим  . Следует учесть, однако, (ср. замечание в пункте 11.1), что географическая широта
. Следует учесть, однако, (ср. замечание в пункте 11.1), что географическая широта 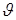 и угол
и угол 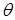 связаны соотношением
связаны соотношением 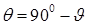 , поэтому в нашем примере
, поэтому в нашем примере  и
и  . Отсюда
. Отсюда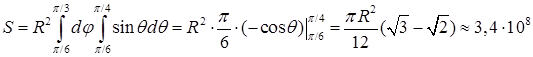 км2.
км2.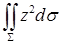 , где
, где 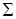 – полная поверхность конуса
– полная поверхность конуса 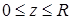 .
. , заданный неравенством
, заданный неравенством 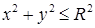 . Поэтому будем вычислять поверхностный интеграл отдельно для основания и для боковой поверхности. На основании
. Поэтому будем вычислять поверхностный интеграл отдельно для основания и для боковой поверхности. На основании  , поэтому интеграл равен
, поэтому интеграл равен 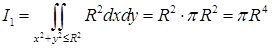 . Для боковой поверхности элемент площади равен
. Для боковой поверхности элемент площади равен  (см. пример 12.3.3). Функция интегрирования
(см. пример 12.3.3). Функция интегрирования 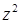 на боковой поверхности равна
на боковой поверхности равна 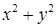 , отсюда поверхностный интеграл равен
, отсюда поверхностный интеграл равен . Интеграл по всей поверхности получим сложением:
. Интеграл по всей поверхности получим сложением: 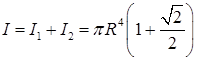 .
.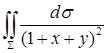 , где
, где 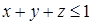 ,
,  ,
, 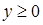 ,
, 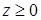 .
.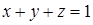 , проектируется на плоскость
, проектируется на плоскость 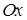 ,
,  и прямой
и прямой 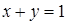 . Уравнение поверхности этой грани
. Уравнение поверхности этой грани  , откуда
, откуда 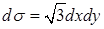 . Таким образом, поверхностный интеграл по этой грани равен
. Таким образом, поверхностный интеграл по этой грани равен 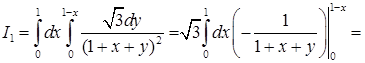
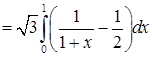
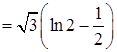 .
.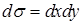 , поэтому
, поэтому 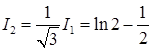 . Интегралы
. Интегралы  и
и 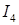 по плоскостям
по плоскостям 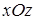 и
и 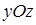 равны.
равны.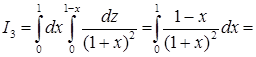
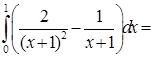
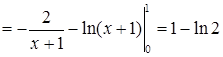 . Здесь мы учли, что на плоскости
. Здесь мы учли, что на плоскости 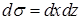 . Теперь найдем окончательный ответ:
. Теперь найдем окончательный ответ: .
.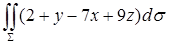 , где
, где 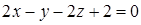 , отсеченная координатными плоскостями.
, отсеченная координатными плоскостями.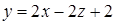 , тогда элемент площади поверхности
, тогда элемент площади поверхности 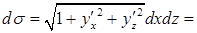
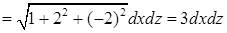 . Проекция поверхности
. Проекция поверхности 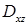 , ограниченным прямой
, ограниченным прямой 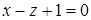 и осями координат. Запишем соответствующий двойной интеграл:
и осями координат. Запишем соответствующий двойной интеграл: 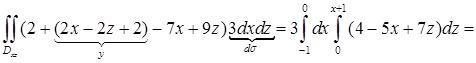

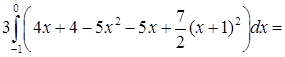

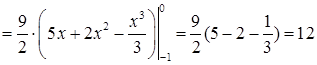 .
. ,
, 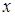 ,
, 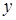 и
и 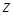 центра масс восьмой части сферы в указанной системе координат совпадают, поэтому найдем значение аппликаты. Воспользуемся выражением элемента площади сферы, вычисленным в пункте 12.1:
центра масс восьмой части сферы в указанной системе координат совпадают, поэтому найдем значение аппликаты. Воспользуемся выражением элемента площади сферы, вычисленным в пункте 12.1: 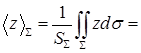

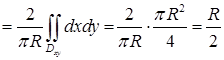 .
. 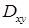 восьмой части сферы на плоскость
восьмой части сферы на плоскость 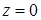 является четвертью круга и имеет площадь
является четвертью круга и имеет площадь 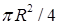 . Итак, центр масс находится в точке
. Итак, центр масс находится в точке 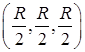 .
.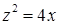 , вырезанной цилиндром
, вырезанной цилиндром 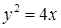 и плоскостью
и плоскостью 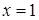 ; б) части гиперболического параболоида
; б) части гиперболического параболоида 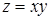 , вырезанной цилиндром
, вырезанной цилиндром  ; в) части
; в) части 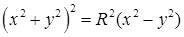 .
. , отсеченной плоскостью
, отсеченной плоскостью 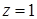 .
. , где
, где 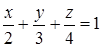 , лежащая в первом октанте.
, лежащая в первом октанте. , где
, где  , где
, где 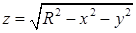 .
.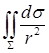 , где
, где 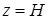 , а
, а 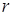 – расстояние от точки цилиндра до начала координат.
– расстояние от точки цилиндра до начала координат.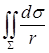 , где
, где 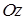 .
.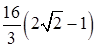 ; б)
; б) 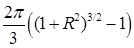 ; в)
; в) 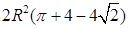 . 12.4.2.
. 12.4.2. 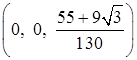 . 12.4.3.
. 12.4.3. 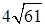 . 12.4.4.
. 12.4.4. 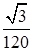 . 12.4.5.
. 12.4.5. 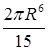 . 12.4.6.
. 12.4.6. 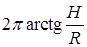 . 12.4.7.
. 12.4.7. 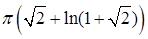 . 12.4.8.
. 12.4.8.  .
.


