
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Решение некоторых типовых задач, рассматриваемых в аудиторииСодержание книги
Поиск на нашем сайте
11.2.1. Вычислить тройной интеграл
Решение. Перепишем уравнения ограничивающих поверхностей, подставляя
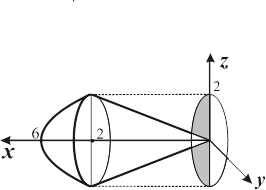
11.2.2. Вычислить объем тела, ограниченного поверхностями
Решение. Найдем сначала линию пересечения конуса ( 11.2.3. Вычислить объем тела, заданного неравенствами
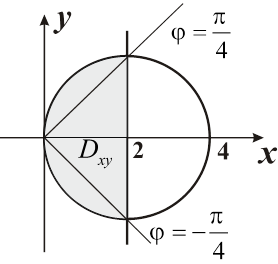
Решение. Первое неравенство уже встречалось в примере 9.3.4 — оно задает круг радиуса
Объем равен 11.2.4. Найти центр масс половины однородного шара радиуса
Решение. Половину шара в декартовых координатах можно задать неравенствами
11.2.5. Найти среднее расстояние от фиксированной точки на границе шара радиуса
Решение. Пусть фиксированная точка, от которой мы будем искать расстояние, расположена в начале координат, а центр шара находится в точке Таким образом, среднее расстояние равно 11.2.6. Найти интеграл Решение. В сферических координатах неравенства, определяющие область, после сокращения на
11.2.7. Вычислить объем тела, ограниченного поверхностью Решение. Для вычисления объема перейдем к сферическим координатам. Уравнение поверхности перепишется так:
11.3. Задачи для самостоятельного решения (ДИСТАНЦИОННОЕ ОБУЧЕНИЕ) 11.3.1. В тройном интеграле 11.3.2. Вычислить с помощью перехода к цилиндрическим или сферическим координатам: а)
11.3.3. Вычислить объем тела, ограниченного поверхностями: а) 11.3.4. Найти центр масс однородного тела, ограниченного поверхностью Ответы. 11.3.1. а) б) в) 11.3.2. а) 11.3.3. а) 11.3.4. ЧАСТЬ В) ДИСТАНЦИОННОЕ ОБУЧЕНИЕ
|
||||||||||
|
Последнее изменение этой страницы: 2021-06-14; просмотров: 195; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.97.150 (0.01 с.) |

 в цилиндрических координатах, если область
в цилиндрических координатах, если область 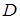 ограничена поверхностями
ограничена поверхностями 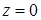 ,
, 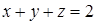 ,
, 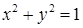 .
.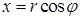 ,
, 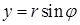 . Получим
. Получим 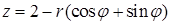 ,
, 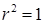 . Подынтегральная функция равна
. Подынтегральная функция равна 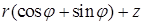 ,
, 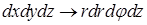 . Пределы интегрирования
. Пределы интегрирования 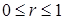 ,
, 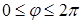 (что соответствует кругу
(что соответствует кругу 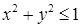 ),
), 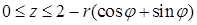 . Теперь можно переходить к вычислению повторного интеграла, записанного в цилиндрических координатах:
. Теперь можно переходить к вычислению повторного интеграла, записанного в цилиндрических координатах: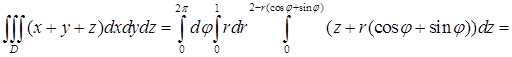
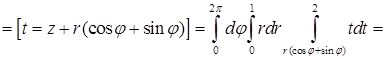
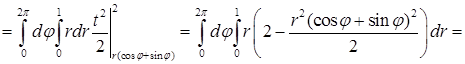
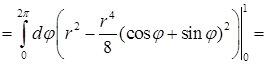

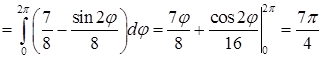 .
.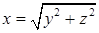 ,
, 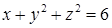 ,
, 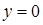 (
(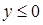 ).
).
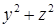 , получим
, получим 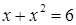 , откуда
, откуда 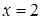
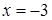 не подходит). Итак, поверхности пересекаются по окружности
не подходит). Итак, поверхности пересекаются по окружности  , лежащей в плоскости
, лежащей в плоскости 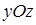 является полукруг
является полукруг 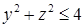 ,
, 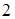 . Введем цилиндрические координаты
. Введем цилиндрические координаты 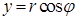 ,
, 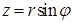 ,
, 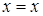 . Перепишем уравнения ограничивающих поверхностей:
. Перепишем уравнения ограничивающих поверхностей:  и
и 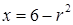 . Очевидно, что при
. Очевидно, что при 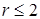 ) имеет место неравенство
) имеет место неравенство 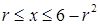 , что определяет пределы интегрирования по
, что определяет пределы интегрирования по 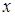 . Пределы интегрирования по
. Пределы интегрирования по 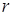 и
и 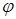 отвечают полукругу при
отвечают полукругу при 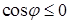 , откуда
, откуда 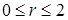 и
и 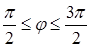 :
: 
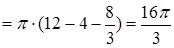 .
.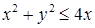 ,
, 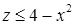 ,
, 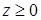 .
.
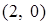 ; пределы интегрирования по
; пределы интегрирования по 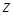 :
: 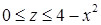 , откуда следует, что
, откуда следует, что 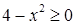 , т. е.
, т. е. 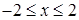 . Таким образом, область интегрирования
. Таким образом, область интегрирования 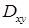 представляет собой полукруг при
представляет собой полукруг при 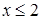 (рис. 11.3). Для вычисления интеграла перейдем к цилиндрическим координатам. Уравнение прямой
(рис. 11.3). Для вычисления интеграла перейдем к цилиндрическим координатам. Уравнение прямой 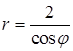 , и это будет верхний предел интегрирования по
, и это будет верхний предел интегрирования по 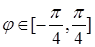 . При значениях угла
. При значениях угла 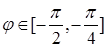 или
или  верхний предел интегрирования по
верхний предел интегрирования по 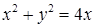 , что дает
, что дает 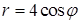 . Верхний предел интеграла по
. Верхний предел интеграла по 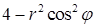 . Объем тела равен
. Объем тела равен 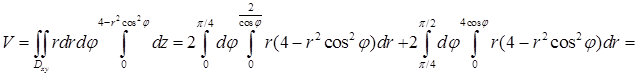
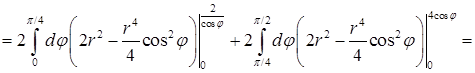
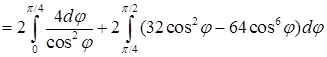 . Вычислим интегралы отдельно. Первый является табличным:
. Вычислим интегралы отдельно. Первый является табличным: 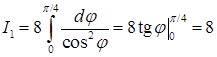 . Во втором преобразуем подынтегральную функцию:
. Во втором преобразуем подынтегральную функцию: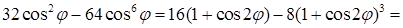

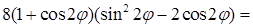
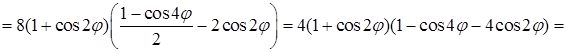
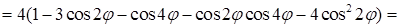
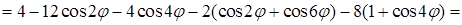
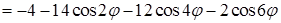 . С такими преобразованиями, основанными на понижении степени тригонометрических функций, приходится часто сталкиваться при вычислениях в цилиндрических и сферических координатах. Теперь найдем второй интеграл:
. С такими преобразованиями, основанными на понижении степени тригонометрических функций, приходится часто сталкиваться при вычислениях в цилиндрических и сферических координатах. Теперь найдем второй интеграл: 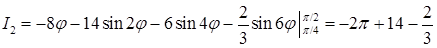 .
.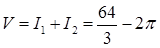 .
. .
.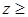 0,
0, 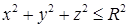 . В цилиндрических координатах второе неравенство примет вид
. В цилиндрических координатах второе неравенство примет вид 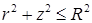 . Из соображений симметрии ясно, что центр масс расположен на оси
. Из соображений симметрии ясно, что центр масс расположен на оси 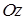 . Осталось найти значение координаты
. Осталось найти значение координаты 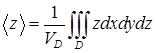 (ср. пример 10.3.8). Вычисление проведем в цилиндрических координатах:
(ср. пример 10.3.8). Вычисление проведем в цилиндрических координатах: 
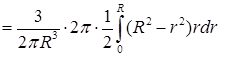
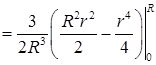
 . Итак, центр масс полушара лежит на его оси на расстоянии
. Итак, центр масс полушара лежит на его оси на расстоянии 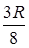 от центра основания.
от центра основания.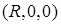 , тогда уравнение сферы, ограничивающей шар, имеет вид
, тогда уравнение сферы, ограничивающей шар, имеет вид 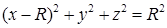 или
или 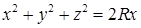 . Вычисления удобно проводить в сферической системе координат. Уравнение сферы принимает вид
. Вычисления удобно проводить в сферической системе координат. Уравнение сферы принимает вид 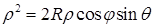 , а неравенство, задающее шар, имеет вид
, а неравенство, задающее шар, имеет вид 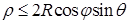 . Но
. Но 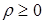 , значит,
, значит, 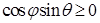 . Для всех
. Для всех 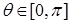
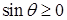 , следовательно,
, следовательно, 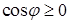 , т. е. угол
, т. е. угол 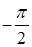 до
до 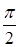 . Требуется найти среднее значение функции
. Требуется найти среднее значение функции 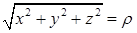 по шару, объем которого
по шару, объем которого  . Среднее значение (ср. пункт 10.2) равно
. Среднее значение (ср. пункт 10.2) равно 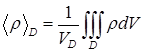 , где элемент объема
, где элемент объема 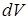 в сферических координатах равен
в сферических координатах равен 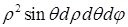 .
. 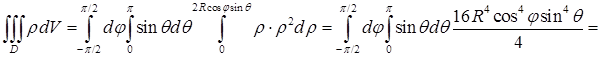
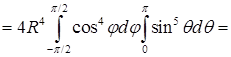
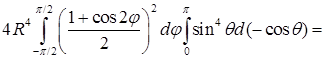
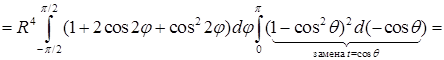
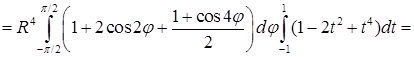
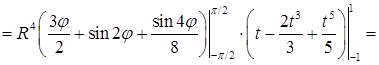
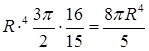 .
.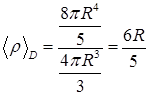 .
.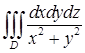 , где область
, где область 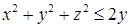 ,
, 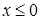 ,
, 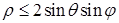 ,
, 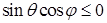 ,
, 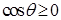 . Отсюда получаем пределы интегрирования по
. Отсюда получаем пределы интегрирования по 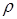 (
(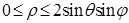 ) и по углам: поскольку
) и по углам: поскольку 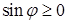 ,
,  , а с учетом
, а с учетом 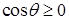 имеем
имеем 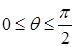 . Перепишем функцию:
. Перепишем функцию:  . Теперь запишем сам интеграл:
. Теперь запишем сам интеграл: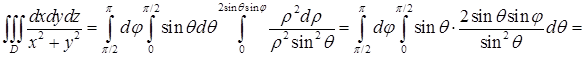
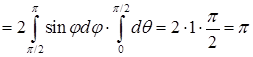 .
.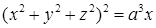 (
( ).
). , или
, или 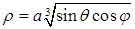 . Нарисовать эту поверхность нелегко (и не нужно!); пределы интегрирования можно определить из неравенства
. Нарисовать эту поверхность нелегко (и не нужно!); пределы интегрирования можно определить из неравенства 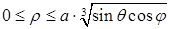 , что дает ограничения по угловым переменным
, что дает ограничения по угловым переменным 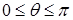 ,
, 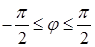 .
.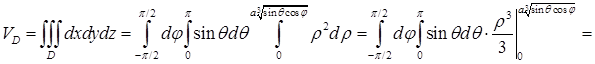
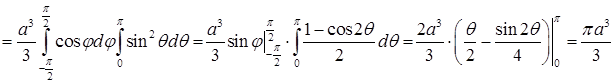 .
.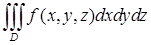 перейти к цилиндрическим или сферическим координатам, если
перейти к цилиндрическим или сферическим координатам, если  , плоскостью
, плоскостью  ; б) часть шара
; б) часть шара  ,
, 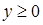 ,
, 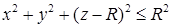 .
.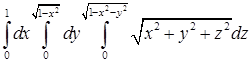 ; б)
; б) 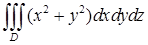 , где область
, где область 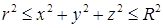 .
.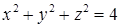 ,
, 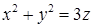
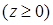 ; б)
; б) 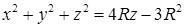 и
и 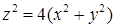 (внутри конуса).
(внутри конуса).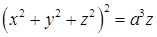 .
. ;
;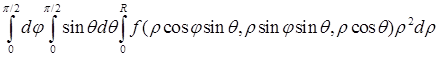 ;
;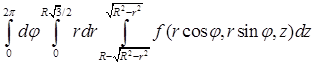 .
. 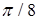 ; б)
; б) 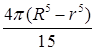 .
. 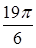 ; б)
; б) 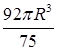 (внутри сферы);
(внутри сферы); 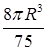 (вне сферы).
(вне сферы).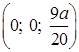 .
.


