Сведение тройного интеграла к двойному

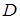Пусть  — область в трехмерном пространстве, и двумерная область  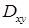— её проекция на плоскость 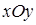. Снизу область  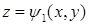ограничена поверхностью , сверху поверхностью 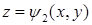. Область  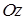также может быть ограничена боковой цилиндрической поверхностью с образующими, параллельными оси  (см. рис. 10.1). Пусть  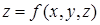— интегрируемая в области  функция трех переменных. Тогда тройной интеграл от этой функции по области  можно свести к повторному следующим образом:

.

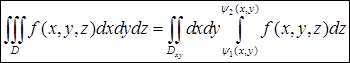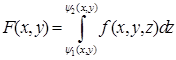После выполнения внутреннего интегрирования получится функция двух переменных , для которой затем надо вычислить двойной интеграл по области : . Внутреннее интегрирование может быть выбрано тремя способами (по 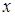, 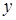или 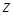), а внешний двойной интеграл по проекции области  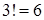на соответствующую координатную плоскость допускает два способа сведения к повторному. Таким образом, для тройного интеграла существует  различных порядков интегрирования. Разумеется, область  должна удовлетворять перечисленным выше требованиям относительно границ, иначе ее необходимо разбить на несколько меньших областей, для каждой из которых тройной интеграл сводится к повторному, а затем интегралы складываются по свойству аддитивности.

Для того, чтобы правильно расставить пределы интегрирования в тройном интеграле, вовсе не обязательно иметь "пространственное воображение". Можно даже обойтись без чертежа. Прежде всего надо выбрать внутреннюю переменную (пусть, к примеру, это будет ), которая допускает ровно два различных выражения из уравнений, определяющих границы области интегрирования. Эти выражения задают верхнюю и нижнюю "крышки" области  (для рис. 10.1 это  и , где ). 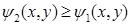Уравнения боковых цилиндрических поверхностей не содержат переменной  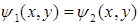и определяют линии на плоскости , которые образуют границу области . Иногда этих линий не хватает, чтобы ограничить конечную область . В таком случае надо найти проекцию линии пересечения "крышек", задаваемую уравнением . Например, если область  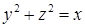ограничена поверхностями  и 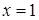, то в качестве переменной внутреннего интегрирования можно взять любую из трех. Если это 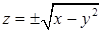, то уравнения "крышек" . Остается уравнение 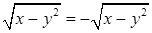, которое не ограничивает конечную область , но вместе с линией пересечения "крышек" (, т. е. 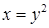) задает параболический сегмент. Расстановка пределов в тройном интеграле имеет вид: 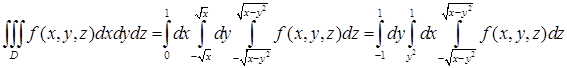. Если в качестве переменной внутреннего интегрирования выбрать, например, , то уравнениями "крышек" будут  и , и граница области 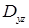 определяется исключительно их линией пересечения 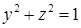, т. е.  является кругом радиуса , а повторный интеграл в этом случае выглядит так: 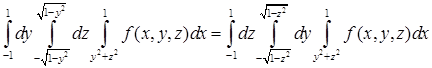. Если не очевидно, какой предел внутреннего интегрирования является верхним, а какой — нижним, то это можно установить, выбрав в области двойного внешнего интегрирования любую "пробную" точку и вычислив в ней значения пределов внутреннего интеграла. 

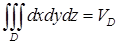Свойства тройного интеграла аналогичны свойствам двойного интеграла с некоторыми поправками. Так, интеграл от единицы дает объем области интегрирования: , и это геометрический смысл тройного интеграла.

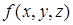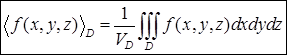Средним арифметическим функции  в области  называется величина .