
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Решение некоторых типовых задач, рассматриваемых в аудитории
10.3.1. Записать тройной интеграл Решение. Очевидно, для внутреннего интегрирования не подойдет переменная Если выбрать для внутреннего интегрирования переменную Другой порядок интегрирования во внешнем двойном интеграле в обоих случаях приводит к сумме двух повторных интегралов. 10.3.2. Расставить пределы интегрирования в Решение. Находим пределы внутреннего интегрирования из уравнения 10.3.3. В повторном интеграле Решение. Пределы внешнего двойного интегрирования определяют область
Теперь примем
10.3.4. Вычислить тройной интеграл
Решение. Внутреннее интегрирование можно выполнить как по переменной
Еще раз отметим, что при расстановке пределов внутреннего интегрирования всегда надо проверять, какой предел является верхним, а какой — нижним. Сделать это можно, взяв в области 10.3.5. Вычислить объем тела, ограниченного координатными плоскостями, плоскостью Решение. Объем тела равен
Теперь область
10.3.6. Вычислить объем тела, ограниченного поверхностями Решение. Выберем для внутреннего интегрирования в 10.3.7. Определить массу пирамиды, ограниченной плоскостями
Решение. Масса тела 10.3.8. Найти центр масс однородного конуса с радиусом основания
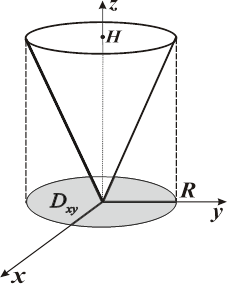
Решение. Центр масс однородного тела имеет координаты, равные средним арифметическим значениям соответствующих координат. Из соображений симметрии понятно, что центр масс прямого кругового конуса лежит на его оси. Осталось найти, на каком расстоянии от вершины. Для этого введем систему координат, как показано на рисунке 10.5. Уравнение боковой поверхности Вычислим интеграл: В последнем интеграле перейдем к полярным координатам, тогда
Объем конуса равен 10.4. Задачи для самостоятельного решения (ДИСТАНЦИОННОЕ ОБУЧЕНИЕ ЧАСТЬ А)) 10.4.1. Вычислить тройные интегралы: а) 10.4.2. Вычислить при помощи тройного интеграла объем тела, ограниченного поверхностями: а) 10.4.3. Найти центр масс однородного тела, ограниченного цилиндрами 10.4.4. Вычислить массу тела, ограниченного прямым круговым цилиндром радиуса Ответы. 10.4.1. а) ЧАСТЬ Б) (ДИСТАНЦИОННОЕ ОБУЧЕНИЕ)
|
||||||||||||||
|
Последнее изменение этой страницы: 2021-06-14; просмотров: 202; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.33.87 (0.019 с.) |
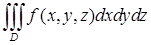 в виде одного повторного всеми возможными способами, если область
в виде одного повторного всеми возможными способами, если область 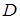 ограничена поверхностями
ограничена поверхностями 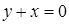 ,
, 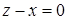 ,
, 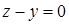 и
и 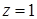 .
.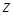 , поскольку она входит в три уравнения границ области
, поскольку она входит в три уравнения границ области 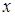 , то пределы внутреннего интеграла — это
, то пределы внутреннего интеграла — это 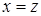 и
и 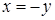 . Оставшиеся уравнения (
. Оставшиеся уравнения ( и
и 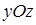 . Найдем проекцию линии пересечения "крышек":
. Найдем проекцию линии пересечения "крышек": 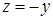 , что вместе с
, что вместе с 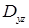 , по которому уже нетрудно расставить пределы. Осталось понять, какой предел внутреннего интегрирования (по
, по которому уже нетрудно расставить пределы. Осталось понять, какой предел внутреннего интегрирования (по 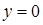 ,
, 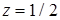 . Подставив эти значения в уравнения "крышек" для
. Подставив эти значения в уравнения "крышек" для 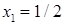 , а для
, а для 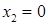 . Значит, первая "крышка" определяет верхний предел интегрирования по
. Значит, первая "крышка" определяет верхний предел интегрирования по 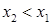 ). С учетом всего сказанного запишем повторный интеграл:
). С учетом всего сказанного запишем повторный интеграл: 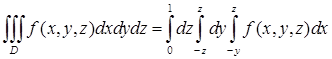 .
.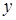 , то совершенно аналогично получим
, то совершенно аналогично получим 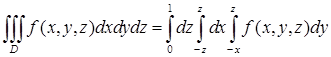 .
.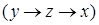 , если область
, если область 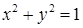 ,
, 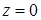 ,
, 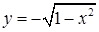 или
или 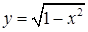 . Эти выражения
. Эти выражения 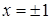 (линии пересечения "крышек"), что вместе с уравнениями
(линии пересечения "крышек"), что вместе с уравнениями 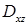 — прямоугольник
— прямоугольник 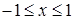 ,
, 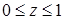 . Повторный интеграл имеет вид
. Повторный интеграл имеет вид 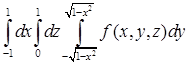 .
.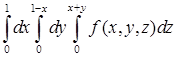 изменить порядок интегрирования на указанный:
изменить порядок интегрирования на указанный: 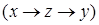 .
.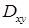 — треугольник
— треугольник 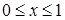 ,
, 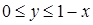 . Внутреннее интегрирование дает ограничение
. Внутреннее интегрирование дает ограничение 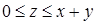 . Таким образом, область интегрирования
. Таким образом, область интегрирования  ,
, 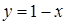 ,
, 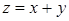 .
.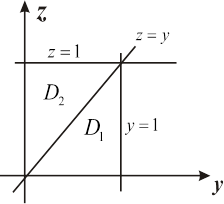
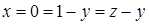 , что дает линии
, что дает линии 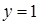 ,
, 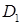 и
и 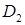 (рис. 10.2). Определим пределы интегрирования по
(рис. 10.2). Определим пределы интегрирования по 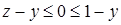 , а в области
, а в области 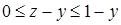 . Таким образом, верхний предел для обеих областей один и тот же:
. Таким образом, верхний предел для обеих областей один и тот же: 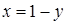 , а нижний меняется при переходе через прямую
, а нижний меняется при переходе через прямую  в области
в области 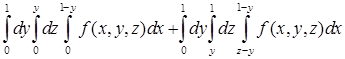 .
. , если область
, если область 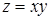 ,
,  ,
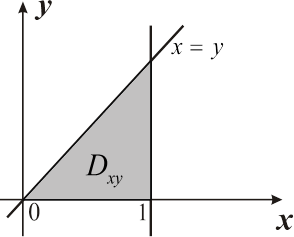
, 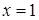 ,
, 
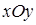 (область
(область 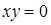 , откуда либо
, откуда либо 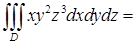
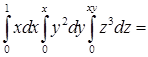
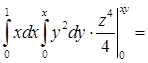
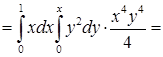
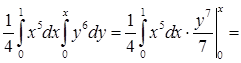
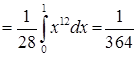 .
.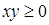 .
.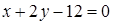 и цилиндром
и цилиндром 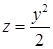 .
.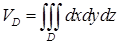 . В уравнениях поверхностей, ограничивающих область интегрирования
. В уравнениях поверхностей, ограничивающих область интегрирования 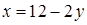 . Теперь определим область внешнего двойного интегрирования
. Теперь определим область внешнего двойного интегрирования 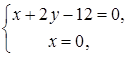 откуда получим
откуда получим 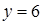 .
.
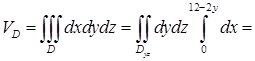
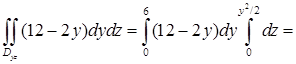
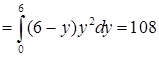 .
. ,
, 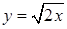 ,
, 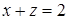 .
.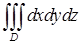 переменную
переменную 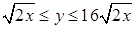 . На плоскости
. На плоскости 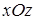 линии
линии 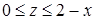 ,
, 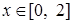 . Запишем повторный интеграл:
. Запишем повторный интеграл: 
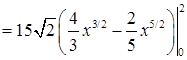
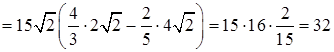 .
.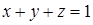 ,
, 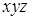 .
.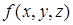 равна интегралу
равна интегралу 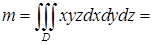

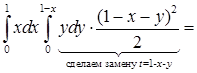
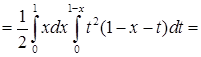
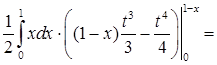
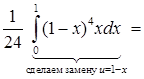
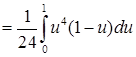
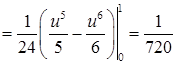 .
. и высотой
и высотой 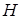 .
.
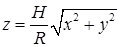 , откуда при
, откуда при 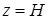 получаем
получаем 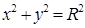 . Проекцией конуса на плоскость
. Проекцией конуса на плоскость 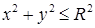 .
.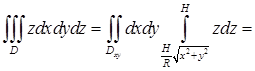
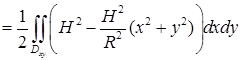 .
.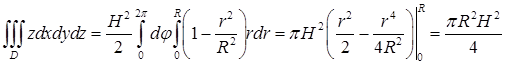 .
.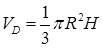 , тогда по формуле для среднего арифметического получим
, тогда по формуле для среднего арифметического получим 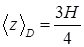 . Итак, центр масс конуса делит его высоту в отношении
. Итак, центр масс конуса делит его высоту в отношении 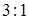 , считая от вершины.
, считая от вершины.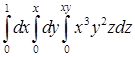 ; б)
; б) 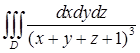 , где
, где 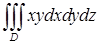 , где область
, где область 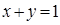 и
и 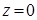 (
(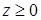 ).
). ,
, 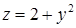 ,
, 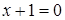 ,
, 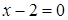 ; б)
; б)  ,
, 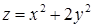 ,
, 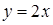 ,
, 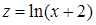 ;
; 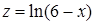 ,
, 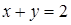 ,
, 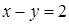 .
.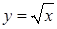 ,
, 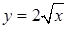 и плоскостями
и плоскостями 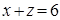 .
.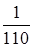 ; б)
; б) 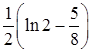 ; в)
; в)  . 10.4.2. а)
. 10.4.2. а) 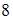 ; б)
; б) 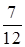 ; в)
; в) 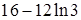 . 10.4.3.
. 10.4.3. 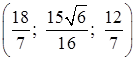 . 10.4.4.
. 10.4.4. 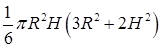 .
. 


