
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Раздел 2. Молекулярная физика. Термодинамика.Содержание книги
Поиск на нашем сайте
Раздел 2. Молекулярная физика. Термодинамика. Тема 2.1. Основы молекулярно-кинетической теории Содержание учебного материала: «Основные положения молекулярно-кинетической теории и их опытное обоснование. Объяснение агрегатных состояний вещества на основе атомно- молекулярных представлений. Модель строения твердых тел. Аморфные вещества и жидкие кристаллы» Цели: Изучить основные положения молекулярно-кинетической теории. Расширить физический кругозор обучающихся. Изучить опытное обоснование МКТ. Ввести основные величины молекулярной физики и соотношения между ними.
Воспитательные: Содействовать формированию фундаментальных преставлений об агрегатных состояниях вещества и об основах МКТ у обучающихся. Воспитывать умение отстаивать собственную точку зрения, сравнивать и делать выводы. Уметь применять полученные теоретические знания на практике. Развивающие: Содействовать развитию и повышению интереса к физике. Содействовать развитию исследовательского мышления и умения ставить демонстрационные опыты. Развить навыки самостоятельной работы у обучающихся. Оборудование: образцы тел различных агрегатных состояний, нагреватель, секундомер, термометр, ёмкости для жидкости и газов.
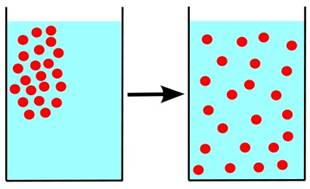
Великому американскому физику Ричарду Фейнману, автору знаменитого курса «Фейнмановские лекции по физике», принадлежат замечательные слова: Если бы в результате какой-то мировой катастрофы все накопленные научные знания оказались бы уничтоженными и к грядущим поколениям живых существ перешла бы только одна фраза, то какое утверждение, составленное из наименьшего количества слов, принесло бы наибольшую информацию? Я считаю, что это — атомная гипотеза (можете называть ее не гипотезой, а фактом, но это ничего не меняет): все тела состоят из атомов — маленьких телец, которые находятся в беспрерывном движении, притягиваются на небольшом расстоянии, но отталкиваются, если одно из них плотнее прижать к другому. В одной этой фразе...содержится невероятное количество информации о мире, стоит лишь приложить к ней немного воображения и чуть соображения. В этих словах заключена суть молекулярно-кинетической теории (МКТ) строения вещества. А именно, основными положениями МКТ являются следующие три утверждения. Любое вещество состоит из мельчайших частиц — молекул и атомов. Они расположены в пространстве дискретно, то есть на некоторых расстояниях друг от друга. Атомы или молекулы вещества находятся в состоянии беспорядочного движения, которое никогда не прекращается. Атомы или молекулы вещества взаимодействуют друг с другом силами притяжения и отталкивания, которые зависят от расстояний между частицами. Эти положения являются обобщением многочисленных наблюдений и экспериментальных фактов. Давайте рассмотрим подробнее эти положения и приведём их опытное обоснование. Атомы и молекулы Возьмём бумажный листок и начнём делить его на всё более и более мелкие части. На каждом ли шаге мы будем получать кусочки именно бумаги, или на каком-то этапе появится нечто новое? Первое положение МКТ говорит нам о том, что вещество не является делимым до бесконечности. Рано или поздно мы дойдём до «последнего рубежа» — мельчайших частиц данного вещества. Эти частицы — атомы и молекулы. Их также можно разделить на части, но тогда исходное вещество прекратит своё существование. Атом — это наименьшая частица данного химического элемента, сохраняющая все его химические свойства. Химических элементов не так много — все они сведены в таблицу Менделеева. Молекула — это наименьшая частица данного вещества (не являющегося химическим элементом), сохраняющая все его химические свойства. Молекула состоит из двух или более атомов одного или нескольких химических элементов. Например, H2O — это молекула воды, состоящая из двух атомов водорода и одного атома кислорода. Разделив её на атомы, мы перестанем иметь дело в веществом под названием «вода». Далее, разделив атомы H и O на составные части, мы получим набор протонов, нейтронов и электронов и тем самым потеряем информацию о том, что поначалу это были водород и кислород. Размер атома или молекулы (состоящей из небольшого числа атомов) составляет порядка 10−8 см. Это настолько малая величина, что атом невозможно разглядеть ни в какой оптический микроскоп. Атомы и молекулы называются для краткости просто частицами вещества. Чем именно является частица — атомом или молекулой — в каждом конкретном случае установить нетрудно. Если речь идёт о химическом элементе, то частицей будет атом; если же рассматривается сложное вещество, то его частица — это молекула, состоящая из нескольких атомов. Далее, первое положение МКТ утверждает, что частицы вещества не заполняют пространство непрерывно. Частицы расположены дискретно, то есть как бы в отдельных точках. Между частицами имеются промежутки, величина которых может меняться в некоторых пределах. В пользу первого положения МКТ свидетельствует явление теплового расширения тел. А именно, при нагревании увеличиваются расстояния между частицами вещества, и размеры тела возрастают. При охлаждении, наоборот, расстояния между частицами уменьшаются, в результате чего тело сжимается. Ярким подтверждением первого положения МКТ служит также диффузия — взаимное проникновение соприкасающихся веществ друг в друга. Например, на рис. 1 показанпроцесс диффузии в жидкости. Частицы растворимого вещества помещены в стакан с водой и расположены вначале в верхней левой части стакана. С течением времени частицы перемещаются (как говорят, диффундируют) из области высокой концентрации в область низкой концентрации. В конце концов концентрация частиц становится везде одинаковой — частицы равномерно распределяются по всему объёму жидкости.
Рис. 1. Диффузия в жидкости Как объяснить диффузию с точки зрения молекулярно-кинетической теории? Очень просто: частицы одного вещества проникают в промежутки между частицами другого вещества. Диффузия идёт тем быстрее, чем больше эти промежутки — поэтому легче всего смешиваются друг с другом газы (в которых расстояния между частицами много больше размеров самих частиц). Газы Газы — самый простой объект для изучения в молекулярно-кинетической теории. Почему? Дело в том, что средние расстояния между частицами газов намного превышают размеры самих частиц. В промежутках между соударениями частицы газа проходят расстояния, на несколько порядков превышающие собственные размеры (рис. 3).
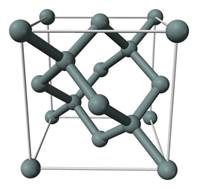
Рис. 3. Частицы газа Например, в воздухе при нормальных условиях длина свободного пробега молекулы составляет примерно 10−5 см. Это на три порядка превышает средний размер молекулы (10−8 см). При таких больших расстояниях между частицами силы межмолекулярного взаимодействия оказываются весьма незначительными. Во многих ситуациях взаимодействием частиц газа на расстоянии можно пренебречь и учитывать лишь их соударения друг с другом. Вот почему изучать газы гораздо проще, чем жидкости или твёрдые тела. Не испытывая сильного притяжения со стороны других частиц, любая частица газа обладает полной свободой передвижения и может оказаться в любом месте сосуда. Поэтому газы не имеют ни фиксированной формы, ни фиксированного объёма. Мы можем поместить данную порцию газа в какой угодно сосуд, и газ неизменно займёт весь предоставленный ему объём. В зависимости от объёма сосуда будут изменяться лишь средние расстояния между частицами газа. Способность газов менять свой объём находит широчайшее применение в технике. Функционирование тепловых двигателей и многих других устройств основано в конечном счёте на том, что газ при расширении перемещает поршень и совершает работу. Твёрдые тела Если сравнивать с газами, то твёрдые тела являются их полной противоположностью. Ни о какой свободе передвижения частицы твёрдых тел даже «не помышляют». В твёрдых телах частицы расположены весьма близко друг к другу: расстояния между частицами порядка размера самих частиц. Силы взаимодействия между частицами твёрдого тела очень велики; расположение частиц в пространстве обладает периодической повторяемостью и образует так называемую кристаллическую решётку. Например, на рис. 4 представлена пространственная модель кристаллической решётки кремния . Шарики — это атомы кремния, а трубки между шариками изображают силы взаимодействия между атомами.
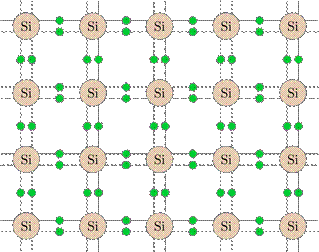
Рис. 4. Пространственная модель кристаллической решётки Атомы кремния, как видите, расположены в пространстве периодическим образом, причём каждый атом сцеплен с четырьмя другими атомами. На рис. 5 мы видим плоское изображение той же самой кристаллической решётки (вдобавок показаны электроны, находящиеся на внешних оболочках атомов кремния).
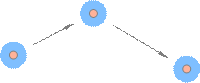
Рис. 5. Плоское изображение кристаллической решётки Точки пространства, в которых находятся частицы твёрдого тела, называются узлами кристаллической решётки. На самом деле частицы не покоятся в узлах кристаллической решётки, а совершают тепловое движение — колеблются относительно этих самых узлов. Таким образом, узел кристаллической решётки — это положение равновесия частицы, в небольшой окрестности которого частица постоянно находится. Чтобы покинуть область своего обитания (выскочить из узла), частице нужна очень большая энергия; произойти такое событие может лишь при чрезвычайно редком стечении обстоятельств. Имея столь жёсткую внутреннюю структуру, твёрдое тело сохраняет неизменными свою форму и свой объём. Жидкости По своим свойствам жидкости занимают промежуточное положение между газами и твёрдыми телами: жидкости сохраняют объём, но не форму. Мы можем говорить об одном литре воды, переливая её из сосуда в сосуд; но при этом вода принимает форму сосуда. Как и в твёрдых телах, частицы жидкости упакованы весьма плотно и совершают колебания около некоторых положений равновесия. Попытка сжатия жидкости немедленно приводит к деформациям самих молекул и встречает мощное сопротивление: жидкости, в отличие от газов, практически не сжимаемы. Однако, в отличие от твёрдых тел, частица жидкости не привязана навсегда к своему положению равновесия: спустя некоторое время она скачком меняет его на новое положение и колеблется в окружении новых частиц. Затем — новый скачок, новый период «осёдлой жизни», и так далее (рис. 6). Если частицы твёрдых тел можно сравнить с людьми, имеющими свой дом, то частицы жидкостей — это кочевники, постоянно меняющие места своих стоянок.
Рис. 6. «Осёдло-кочевая жизнь» молекулы жидкости На рисунке мы видим молекулу жидкости, время от времени меняющую место своего расположения. «Ореол», окружающий молекулу, изображает область осёдлой жизни, внутри которой молекула совершает тепловые колебания. Теоретические расчёты показывают, что за время осёдлой жизни молекула совершает несколько десятков-сотен колебаний внутри области осёдлой жизни. Силы притяжения между частицами жидкости достаточно велики для того, чтобы объём сохранялся фиксированным. Но ограниченность времени осёдлой жизни частиц придаёт жидкостям текучесть: жидкости не сохраняют форму. Рассмотрим для примера воду в стакане. Скачки молекул из одного осёдлого положения в другое происходят равновероятно по всем направлениям. Но если стакан наклонить, то в определённых участках воды сила тяжести задаст преимущественное направление этих скачков, и форма воды в стакане поменяется. Таково в общих чертах объяснение текучести. Введём основные величины молекулярной физики и соотношения между ними. m — масса вещества, V — объём вещества, m = ρV. N — число частиц вещества (атомов или молекул). m 0 — масса частицы вещества. Тогда m = m 0 N.
N = nV. Что получится, если m 0 умножить на n? Произведение массы частицы на число частиц в единице объёма даст массу единицы объёма, т.е. плотность. Формально:
Итак, ρ = m 0 n. Массы и размеры частиц невообразимо малы по нашим обычным меркам. Например, масса атома водорода порядка 10−24 г, размер атома порядка 10−8 см. Из-за столь малых значений масс и размеров число частиц в макроскопическом теле огромно. Оперировать столь грандиозными числами, как число частиц, неудобно. Поэтому для измерения количества вещества используют специальную единицу — моль. Один моль — это количество вещества, в котором содержится столько же атомов или молекул, сколько атомов содержится в 12 граммах углерода. А в 12 граммах углерода содержится примерно 6, 02 · 1023 атомов. Стало быть, в одном моле вещества содержится 6, 02 · 1023 частиц. Это число называется постоянной Авогадро: N A = 6, 02 · 1023 моль−1. Количество вещества обозначается ν. Это число молей данного вещества. Что получится, если ν умножить на N A? Число молей, умноженное на число частиц в моле, даст общее число частиц: N = νN A. Масса одного моля вещества называется молярной массой этого вещества и обозначается µ ([ µ ] = кг/моль). Ясно, что m = µν. Как найти молярную массу химического элемента? Оказывается, для этого достаточно заглянуть в таблицу Менделеева! Нужно просто взять атомную массу A (число нуклонов) данного элемента — это будет его молярная масса, выраженная в г/моль. Например, для алюминия A = 27, поэтому молярная масса алюминия равна 27 г/моль или 0,027 кг/моль. Почему так получается? Очень просто. Молярная масса углерода равна 12 г/моль по определению. В то же время ядро атома углерода содержит 12 нуклонов. Выходит, что каждый нуклон вносит в молярную массу 1 г/моль. Поэтому молярная масса химического элемента с атомной массой A оказывается равной A г/моль. Молярная масса вещества, молекула которого состоит из нескольких атомов, получается простым суммированием молярных масс. Так, молярная масса углекислого газа CO2 равна 12 + 16 · 2 = 44 г/моль = 0, 044 кг/моль. Будьте внимательны с молярными массами некоторых газов! Так, молярная масса газообразного водорода равна 2 г/моль, поскольку его молекула состоит из двух атомов (H2). То же касается часто встречающихся в задачах азота и кислорода (N2, O2). Вместе с тем, наиболее частый персонаж задач — гелий (He) — является одноатомным газом и имеет молярную массу 4 г/моль, предписанную таблицей Менделеева. Ещё раз предостережение: при расчётах не забывайте переводить молярную массу в кг/моль! Если ваш ответ отличается от правильного на три порядка, то вы наверняка сделали именно эту, очень распространённую ошибку:-) Что получится, если m 0 умножить на N A? Масса частицы, умноженная на число частиц в моле, даст массу моля, т. е. молярную массу: µ = m 0 N A.
Решение задач.
Задача №1 Какова масса 500 моль углекислого газа? Дано: Решение:
m-? Ответ:22 кг Задача №2 Задача №3 Решение задач Задача №1 При какой температуре средняя кинетическая энергия поступательного движения молекул газа равна 6,21*10-21 Дж?
Дано: Решение:
Т-? Ответ:300 K З адача №2 При какой температуре средняя квадратичная скорость молекул азота 830 м/с? Дано: Решение:
Т-? m0= Т= Ответ:774 K
Задача №3 Какова средняя квадратичная скорость молекул кислорода при температуре 300К?
Vср-? m0= V= Ответ: 473м/с
Содержание учебного материала: «Уравнение состояния идеального газа. Изопроцессы. Газовые законы.» Цели. Учебные: Сформировать специальные знания, умения и навыки по заданной теме. Раскрыть сущность уравнения Менделеева – Клайперона, изопроцессов и газовых законов. Научить строить графики изопроцессов. Научить применять газовые законы при решении практических и графических задач. Воспитательные: Воспитывать трудолюбие, интерес к предмету, внимательность и наблюдательность. Прививать навыки работы в должном темпе, развивать инициативу, уверенность в своих силах. Повысить интерес обучающихся к изучаемому материалу путем разнообразия форм проведения уроков. Развивающие: Развивать познавательные способности обучающихся. Активизировать исследовательские способности. Расширять их кругозор, исследовательское мышление. Уметь применять полученные теоретические знания на практике. Развить умения слушать, анализировать, чётко аргументировать, излагать и отстаивать своё мнение. Оборудование: манометр, термометр, весы, нагреватель, ёмкость для нагревания жидкости, градуированный сосуд, секундомер, измерительная лента. Берём формулу p = nkT. Вспомним теперь, что
откуда pV = νRT. (3) Соотношение (3) называется уравнением Менделеева — Клапейрона. Оно даёт взаимосвязь трёх важнейших макроскопических параметров, описывающих состояние идеального газа — давления, объёма и температуры. Поэтому уравнение Менделеева — Клапейрона называется ещё уравнением состояния идеального газа. Учитывая, что
Есть ещё один полезный вариант этого уравнения. Поделим обе части на V:
Но
В задачах по физике активно используются все три формы записи (3)—(5). На протяжении этого раздела мы будем придерживаться следующего предположения: масса и химический состав газа остаются неизменными. Иными словами, мы считаем, что: m = const, то есть нет утечки газа из сосуда или, наоборот, притока газа в сосуд; µ = const, то есть частицы газа не испытывают каких-либо изменений (скажем, отсутствует диссоциация — распад молекул на атомы). Эти два условия выполняются в очень многих физически интересных ситуациях (например, в простых моделях тепловых двигателей) и потому вполне заслуживают отдельного рассмотрения. Если масса газа и его молярная масса фиксированы, то состояние газа определяется тремя макроскопическими параметрами: давлением, объёмом и температурой. Эти параметры связаны друг с другом уравнением состояния (уравнением Менделеева — Клапейрона). Термодинамический процесс Термодинамический процесс (или просто процесс) — это изменение состояния газа с течением времени. В ходе термодинамического процесса меняются значения макроскопических параметров — давления, объёма и температуры. Особый интерес представляют изопроцессы — термодинамические процессы, в которых значение одного из макроскопических параметров остаётся неизменным. Поочерёдно фиксируя каждый из трёх параметров, мы получим три вида изопроцессов. Изотермический процесс идёт при постоянной температуре газа: T = const. Изобарный процесс идёт при постоянном давлении газа: p = const. Изохорный процесс идёт при постоянном объёме газа: V = const. Изопроцессы описываются очень простыми законами Бойля — Мариотта, Гей-Люссака и Шарля. Давайте перейдём к их изучению. Изотермический процесс При изотермическом процессе температура газа постоянна. В ходе процесса меняются только давление газа и его объём. Установим связь между давлением p и объёмом V газа в изотермическом процессе. Пусть температура газа равна T. Рассмотрим два произвольных состояния газа: в одном из них значения макроскопических параметров равны p 1 ,V 1 ,T, а во втором — p 2 ,V 2 ,T. Эти значения связаны уравнением Менделеева — Клапейрона:
Как мы сказали с самого начала, масса газа m и его молярная масса µ предполагаются неизменными. Поэтому правые части выписанных уравнений равны. Следовательно, равны и левые части: p 1 V 1 = p 2 V 2. Поскольку два состояния газа были выбраны произвольно, мы можем заключить, что в ходе изотермического процесса произведение давления газа на его объём остаётся постоянным: pV = const. Данное утверждение называется законом Бойля — Мариотта. Записав закон Бойля — Мариотта в виде const p = V можно дать и такую формулировку: в изотермическом процессе давление газа обратно пропорционально его объёму. Если, например, при изотермическом расширении газа его объём увеличивается в три раза, то давление газа при этом в три раза уменьшается. Как объяснить обратную зависимость давления от объёма с физической точки зрения? При постоянной температуре остаётся неизменной средняя кинетическая энергия молекул газа, то есть, попросту говоря, не меняется сила ударов молекул о стенки сосуда. При увеличении объёма концентрация молекул уменьшается, и соответственно уменьшается число ударов молекул в единицу времени на единицу площади стенки — давление газа падает. Наоборот, при уменьшении объёма концентрация молекул возрастает, их удары сыпятся чаще и давление газа увеличивается. Изобарный процесс Напомним ещё раз, что изобарный процесс — это процесс, проходящий при постоянном давлении. В ходе изобарного процесса меняются лишь объём газа и его температура. Типичный пример изобарного процесса: газ находится под массивным поршнем, который может свободно перемещаться. Если масса поршня M и поперечное сечение поршня S, то давление газа всё время постоянно и равно
где p 0 — атмосферное давление. Пусть идеальный газ совершает изобарный процесс при давлении p. Снова рассмотрим два произвольных состояния газа; на этот раз значения макроскопических параметров будут равны p,V 1 ,T 1 и p,V 2 ,T 2. Выпишем уравнения состояния:
Поделив их друг на друга, получим:
В принципе, уже и этого могло бы быть достаточно, но мы пойдём немного дальше. Перепишем полученное соотношение так, чтобы в одной части фигурировали только параметры первого состояния, а в другой части — только параметры второго состояния (иными словами, «разнесём индексы» по разным частям):
А отсюда теперь — ввиду произвольности выбора состояний! — получаем закон Гей-Люссака:
Иными словами, при постоянном давлении газа его объём прямо пропорционален температуре: V = const · T. Почему объём растёт с ростом температуры? При повышении температуры молекулы начинают бить сильнее и приподнимают поршень. При этом концентрация молекул падает, удары становятся реже, так что в итоге давление сохраняет прежнее значение. Графики изобарного процесса График изобарного процесса называется изобарой. На V T -диаграмме изобара V = const · T является прямой линией (рис. 10):
Рис. 10. Изобара на V T -диаграмме Изохорный процесс Изохорный процесс, напомним, — это процесс, проходящий при постоянном объёме. При изохорном процессе меняются только давление газа и его температура. Изохорный процесс представить себе очень просто: это процесс, идущий в жёстком сосуде фиксированного объёма (или в цилиндре под поршнем, когда поршень закреплён). Пусть идеальный газ совершает изохорный процесс в сосуде объёмом V. Опять-таки рассмотрим два произвольных состояния газа с параметрами p 1 ,V,T 1 и p 2 ,V,T 2. Имеем:
Делим эти уравнения друг на друга:
Как и при выводе закона Гей-Люссака, «разносим» индексы в разные части:
Ввиду произвольности выбора состояний мы приходим к закону Шарля:
Иными словами, при постоянном объёме газа его давление прямо пропорционально температуре: p = const · T. Увеличение давления газа фиксированного объёма при его нагревании — вещь совершенно очевидная с физической точки зрения. Вы сами легко это объясните. Графики изохорного процесса График изохорного процесса называется изохорой. На pT -диаграмме изохора p = const · T является прямой линией (рис. 13):
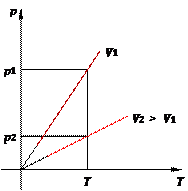
Рис. 13. Изохора на pT -диаграмме Смысл пунктирного участка тот же: неадекватность модели идеального газа при низких температурах. Далее, чем больше объём, тем ниже идёт изохора на pT -диаграмме (рис. 14):
Рис. 14. Чем ниже изохора, тем больше объём Количество теплоты Как мы знаем, одним из способов изменения внутренней энергии является теплопередача (теплообмен). Предположим, что тело участвует в теплообмене с другими телами, и при этом не совершается механическая работа — ни самим телом, ни другими телами над этим телом. Если в процессе теплообмена внутренняя энергия тела изменилась на величину ∆ U, то говорят, что тело получило соответствующее количество теплоты: Q = ∆ U. Если при этом величина ∆ U отрицательна, т.е. тело отдавало энергию, то говорят также, что тело отдавало тепло. Например, вместо формально верной, но несколько нелепой фразы «тело получило −5 Дж тепла» мы скажем: «тело отдало 5 Дж тепла». Уравнение теплового баланса Рассмотрим два тела (обозначим их 1 и 2), которые образуют замкнутую систему. Это означает, что данные тела могут обмениваться энергией только друг с другом, но не с другими телами. Считаем также, что механическая работа не совершается — внутренняя энергия тел меняется только в процессе теплообмена. Имеется фундаментальный закон природы, подтверждаемый всевозможными экспериментами — закон сохранения энергии. Он гласит, что полная энергия замкнутой системы тел не меняется со временем. В данном случае закон сохранения энергии утверждает, что внутренняя энергия нашей системы будет оставаться одной и той же: U 1 + U 2 = const. Если изменение внутренней энергии первого тела равно ∆ U 1, а изменение внутренней энергии второго тела равно ∆ U 2, то суммарное изменение внутренней энергии будет равно нулю: ∆ U 1 + ∆ U 2 = 0. Но ∆ U 1 = Q 1 — количество теплоты, полученное первым телом в процессе теплообмена; аналогично ∆ U 2 = Q 2 — количество теплоты, полученное вторым телом в процессе теплообмена. Стало быть, Q 1 + Q 2 = 0 . (7) Попросту говоря, сколько дожулей тепла отдало одно тело, ровно столько же джоулей получило второе тело. Так как система замкнута, ни один джоуль наружу не вышел. Соотношение (7) называется уравнением теплового баланса. В общем случае, когда n тел образуют замкнутую систему и обмениваются энергией только с помощью теплопередачи, из закона сохранения энергии с помощью тех же рассуждений получаем общее уравнение теплового баланса: Q 1 + Q 2 + ... + Qn = 0 . (8) В качестве простого примера применения уравнения теплового баланса рассмотрим следующую задачу. Смешали m 1 = 200 г воды при температуре t 1 = 100◦C и m 2 = 300 г воды при температуре t 2 = 20◦C. Найти установившуюся температуру смеси. Обозначим искомую установившуюся температуру через θ. Запишем уравнение теплового баланса (7): cm 1(θ − t 1) + cm 2(θ − t 2) = 0, где c — удельная теплоёмкость воды. Раскрываем скобки и находим:
Удельная теплота плавления Итак, для превращения твёрдого тела в жидкость мало довести его до температуры плавления. Необходимо дополнительно (уже при температуре плавления) сообщить телу некоторое количество теплоты Q плдля полного разрушения кристаллической решётки (т.е. для прохождения участка BC). Это количество теплоты идёт на увеличение потенциальной энергии взаимодействия частиц. Следовательно, внутренняя энергия расплава в точке C больше внутренней энергии твёрдого тела в точке B на величину Q пл. Опыт показывает, что величина Q плпрямо пропорциональна массе тела: Q пл= λm. Коэффициент пропорциональности λ не зависит от формы и размеров тела и является характеристикой вещества. Он называется удельной теплотой плавления вещества. Удельную теплоту плавления данного вещества можно найти в таблицах. Удельная теплота плавления численно равна количеству теплоты, необходимому для превращения в жидкость одного килограмма данного кристаллического вещества, доведённого до температуры плавления. Так, удельная теплота плавления льда равна 340 кДж/кг, свинца — 25 кДж/кг. Мы видим, что для разрушения кристаллической решётки льда требуется почти в 14 раз больше энергии! Лёд относится к веществам с большой удельной теплотой плавления и поэтому весной тает не сразу. Парообразование и конденсация Парообразование — это переход жидкости в газообразное состояние (в пар). Существует два способа парообразования: испарение и кипение. Испарением называется парообразование, которое происходит при любой температуре со свободной поверхности жидкости. Как вы помните из листка «Насыщенный пар», причиной испарения является вылет из жидкости наиболее быстрых молекул, которые способны преодолеть силы межмолекулярного притяжения. Эти молекулы и образуют пар над поверхностью жидкости. Разные жидкости испаряются с разными скоростями: чем больше силы притяжения молекул друг к другу — тем меньшее число молекул в единицу времени окажутся в состоянии их преодолеть и вылететь наружу, и тем меньше скорость испарения. Быстро испаряются эфир, ацетон, спирт (их иногда называют летучими жидкостями), медленнее — вода, намного медленнее воды испаряются масло и ртуть. Скорость испарения растёт с повышением температуры (в жару бельё высохнет скорее), поскольку увеличивается средняя кинетическая энергия молекул жидкости, и тем самым возрастает число быстрых молекул, способных покинуть её пределы. Скорость испарения зависит от площади поверхности жидкости: чем больше площадь, тем большее число молекул получают доступ к поверхности, и испарение идёт быстрее (вот почему при развешивании белья его тщательно расправляют). Одновременно с испарением наблюдается и обратный процесс: молекулы пара, совершая беспорядочное движение над поверхностью жидкости, частично возвращаются обратно в жидкость. Превращение пара в жидкость называется конденсацией. Конденсация замедляет испарение жидкости. Так, в сухом воздухе бельё высохнет быстрее, чем во влажном. Быстрее оно высохнет и на ветру: пар сносится ветром, и испарение идёт более интенсивно. В некоторых ситуациях скорость конденсации может оказаться равной скорости испарения. Тогда оба процесса компенсируют друг друга и наступает динамическое равновесие: из плотно закупоренной бутылки жидкость не улетучивается годами, а над поверхностью жидкости в этом случае находится насыщенный пар. Конденсацию водяного пара в атмосфере мы постоянно наблюдаем в виде облаков, дождей и выпадающей по утрам росы; именно испарение и конденсация обеспечивают круговорот воды в природе, поддерживая жизнь на Земле. Поскольку испарение — это уход из жидкости самых быстрых молекул, в процессе испарения средняя кинетическая энергия молекул жидкости уменьшается, т.е. жидкость остывает. Вам хорошо знакомо ощущение прохлады и порой даже зябкости (особенно при ветре), когда выходишь из воды: вода, испаряясь по всей поверхности тела, уносит тепло, ветер же ускоряет процесс испарения[5]. Ту же прохладу можно почувствовать, если провести по руке кусочком ваты, смоченным в летучем растворителе (скажем, в ацетоне или жидкости для снятия лака). В сорокаградусную жару благодаря усиленному испарению влаги через поры нашего тела мы сохраняем свою температуру на уровне нормальной; не будь этого терморегулирующего механизма, в такую жару
|
||||||
|
Последнее изменение этой страницы: 2021-06-14; просмотров: 181; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.137 (0.017 с.) |


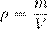 — плотность вещества (масса единицы объёма). Отсюда
— плотность вещества (масса единицы объёма). Отсюда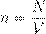 — концентрация вещества (число частиц в единице объёма), [ n ] = м−3. Отсюда
— концентрация вещества (число частиц в единице объёма), [ n ] = м−3. Отсюда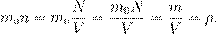

 υ = 500 моль υ =
υ = 500 моль υ = 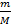 => m=υ*M=500*44*10-3=22000*10-3=22 кг
=> m=υ*M=500*44*10-3=22000*10-3=22 кг
 Ек=6,21*10-21 Дж Eк=
Ек=6,21*10-21 Дж Eк= 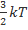 =>
=> 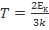 =
= 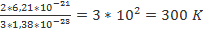

 V=830м/с V=
V=830м/с V= 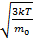 => T=
=> T= 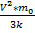
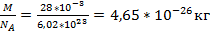
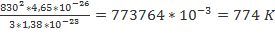
 Дано: Решение:
Дано: Решение: Т=300К V=
Т=300К V= 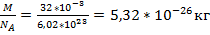
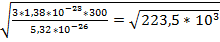 =473м/с
=473м/с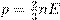 и подставляем в неё
и подставляем в неё 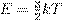 . Получаем:
. Получаем: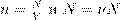
 A, где ν — число молей газа:
A, где ν — число молей газа: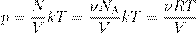 ,
, , где m — масса газа, получим другую форму уравнения Менделеева — Клапейрона:
, где m — масса газа, получим другую форму уравнения Менделеева — Клапейрона: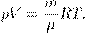 (4)
(4)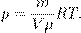
 — плотность газа. Отсюда
— плотность газа. Отсюда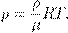 (5)
(5)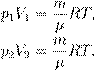
 ,
,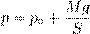 ,
,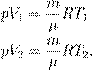 ,
,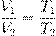 .
. .
. = const.
= const.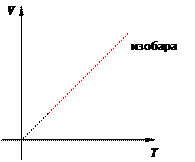
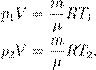 ,
,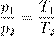 .
. .
.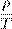 = const.
= const.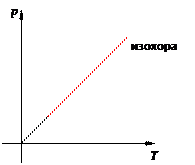
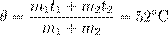 .
.


