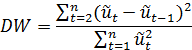Алгоритм теста Дарбина–Уотсона. Условия применимости теста DW .

Тест предназначен для проверки предпосылки Cov(ui;uj)=0, i не=j (1) теоремы Гаусса – Маркова, а точнее важнейшего частного случая этой предпосылки, а именно статистической гипотезы

H0: Cov(ui;uj)=0, при j=i-1 (2).

Неадекватность гипотезы (2) влечет неадекватность предпосылки (1), что влечет за собой негативные последствия для МНК-оценок параметров модели.

ШАГ1. По уравнения наблюдений объекта следует вычислить МНК-оценки и оценки случайных остатков.

ШАГ2. Вычислить величину:

ШАГ3. Из таблицы, составленной Дарбиным и Уотсоном выбираем по n и k значения dl и du.

ШАГ4. Проверить в какое подмножество попала величина DW, при условии, что (0;dl) – Cov(ui;uj)>0 (Положительная автокорреляция)

(dl;du) неопределенность, необходимо исследование по бОльшей выборке

(du;4-du) – Cov(ui;uj)=0, случайные остатки не связаны между собой

(4-du;4-dl) неопределенность

(4-dl;4) - Cov(ui;uj)<0 (Отрицательная автокорреляция)

УСЛОВИЯ ПРИМЕНИМОСТИ:

(8.17) – это предпосылка о нулевом мат.ожидании остатков

(8.18)- о равенстве дисперсий остатков между собой

(8.20) – о нулевой ковариации регрессоров и остатков

Влияние автокорреляции на оценку параметров модели. Методы устранения автокорреляции: при известном коэффициенте корреляции

Если оценивать параметры уравнения, не принимая во внимание автокорреляцию в остатках, и, следовательно, оценивать параметры a и b обычным методом МНК, то полученные оценки будут неэффективны. Т.к. они не будут иметь минимальную дисперсию. МНК-оценка дисперсии теряет свойство несмещенности. Это приводит к увеличению стандартных ошибок, снижению фактических значений t-критерия и широким доверительным интервалам для коэффициента регрессии. На основе таких результатов можно сделать ошибочный вывод о незначимом влиянии исследуемого фактора на результат, в то время как на самом деле его влияние статистически значимо.

Отметим, что при соблюдении прочих предпосылок МНК автокорреляция остатков не влияет на свойства состоятельности и несмещенности оценок параметров уравнения регрессии обычным МНК, за исключением моделей авторегрессии.

Методы устранения автокорреляции: при известном коэффициенте корреляции – ОМНК, метод максимального правдоподобия.

 

Мы предположили, что р известно. Тогда можно вычислить величины y~t, x~t, и qt (последняя одинакова для всех наблюдений) для наблюдений, включающих от 2 до Т исходных данных. Если теперь оценить регрессию между yt, xt и qt (заметим, что в уравнение не должна включаться постоянная), то будут получены оценки а и р, не связанные с проблемой автокорреляции, поскольку, согласно предположению, значения г не зависят друг от друга.

 

Остается, однако, небольшая проблема. Если в выборке нет данных, предшествующих первому наблюдению, то мы не сможем вычислить у{ и хх и потеряем первое наблюдение. Число степеней свободы уменьшается на единицу, и это вызовет потерю эффективности, которая может в небольших выборках перевесить повышение эффективности от устранения автокорреляции.