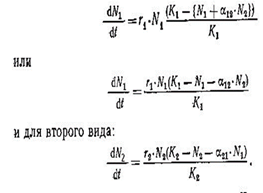Межвидовая конкуренция, уравнение межвидовой конкуренции Лотки-Вольтеры.

Конкуренция –это любое взаимодействие между популяциями двух и более видов, которое неблагоприятно сказывается на их росте и выживании.

    Принцип конкурентного исключения (принцип Гаузе) гласит: если два вида конкурируют за одну нишу, есть только два возможных исхода. Либо эти два вида немного изменятся и каждый займет немного другую нишу (дифференциация ниш), либо один из видов обречен на вымирание. Межвидовая конкуренция не является средством популяционного контроля и стабильности (в отличие от внутривидовой конкуренции) (опыт Гаузе, инфузории 2 близкородственных вида, в одинаковых условиях и место обитаний не могут жить вместе одна вытеснит другую, но при смене обитаний оба вида смогут существовать совместно)

    Межвидовая конкуренция может играть важную роль в формировании облика природного сообщества. Порождая и закрепляя разнообразие организмов, конкуренция способствует повышению устойчивости сообществ, более эффективному использованию имеющихся ресурсов.

Модель Лотки-Вольтера (уравнения роста двух популяций)

(в ограниченном пространстве, где для каждой популяции имеется определенный уровень равновесия (максимальная емкость среды для вида (предельная плотность насыщения) - К, N1 N2-чисоенности видов 1 и 2, a- коэффициент конкуренции, характеризующий давление вида 2 на вид 1 (ингибирующий воздействие вид 2 на вид1), b-коэффициент конкур, давление вида 1 на вид 2 (ингибирование (предотвращение, замедление) вида 2 видом1). r – биотический потенциал (максимальная врожденная скорость роста популяции.

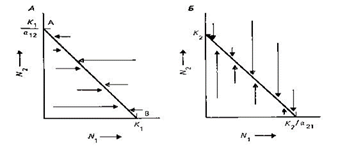
На диаграммах значения N1 отложены по горизонтальной, а N2 по вертикальной осям, так что численность обоих видов снижается вниз и влево, а повышается вверх и вправо. Одни сочетания будут N1 и N2 будут вызывать увеличение численности вида 1 и (или) вида 2, тогда как другие – уменьшение численности вида 1 и (или) вида 2; кроме того, для каждого вида можно провести изоклины (линии, вдоль которых не наблюдается ни увеличение, ни уменьшения численности), отделяющие сочетание численности, при которых наблюдается рост популяции, от тех сочетании при которых популяция сокращается. Для того, чтобы провести изоклину для вида 1, берём из уравнения dN1 /dt=0. r1 N1 (K 1-N 1-α12*N 2) =0 это справедливо, когда врожденная удельная скорость роста популяции r1 и N1 =0. K1 –N1- α12*N2=0 или N1= K1 –α12*N2. другими словами, в любой точке прямой, которое описывает уравнение dN1 /dt=0 → линия является изоклиной для вида 1;

А поскольку эта линия представляет собой прямую, то её можно провести, определив всего две точки и затем соединив из при N1 = 0 N2 = K1/α12 (точка А), при N2 = 0 N1 = K1 (точка В). Соединив их, получили изоклину для вида 1. Вниз и влево от этой линии численность обоих видов относительно невелика и вид 1, испытывая слабую конкуренцию увеличивает свою численность (стрелки направлены слева направо). Вверх и вправо от линии общая численность увеличивается и численность вида 1 снижается. Чтобы определить исход конкуренции надо объединить эти 2 изоклины → K1/ α 12> K2 и K1> K2/ α21; K1> α 12 *K2 и K* α21 > K1. первоначальное неравенство показывает, что ингибирующие влияние внутривидовой конкуренции выражено сильнее, чем межвидовое воздействие вида 2 на вид 1. Второе неравенство, если вид 1 может оказывать большее влияние на вид 2, чем последний сам на себя. Т.О., вид 1 является более сильным конкурентам в межвидовой борьбе, чем вид 2; вид 1 приводит вид 2 к вымиранию, а сам достигает предельной плотности насыщения. K2>K1/α12 и K1 > K2 / α21; K2 * α12 >K1 и K1 * α21 > K2. Оба вида сильнее влияют на конкурента, чем сами страдают от внутривидовой конкуренции. Такое может быть, например, если каждый вид выделяет вещества ядовитые для конкурента, но безвредное для самого себя, вследствие этого является неустойчивым равновесная комбинация из N1 и N2 (где изоклины пересекаются) и 2 устойчивые точки. В первой из них численность вида 1 достигает предельной, а вид 2 вымирает; во второй точке ситуация противоположная. Исход конкуренции, которой будет, достигнут в действительности, зависит от величины начальной плотности: вид, который имеет преимущества в начале, будет вытеснять конкурента до полного исчезновения. В целом на модели Лотки-Вольтера можно получить: безусловное исключение одного вида другим, исключение в зависимости от соотношения величин начальной плотности и устойчивое сосуществование. Выводы: в ходе взаимодействия, безусловно, возможны исключения одного вида другим; исключения в зависимости от величины начальной плотности популяции и величины конкурентной силы.

Исключения из правила конкурентного исключения

При обильном ресурсе (растительная масса – фитофаги в летний сезон) конкурентные отношения между фитофагами не завершаются конкурентным исключением в следствие абиотических нарушений среды и влияния хищников.