Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод введення нових змінних.Содержание книги
Поиск на нашем сайте
Приклад 4. Розв’яжіть систему
Розв’язування. Розв’яжемо дану систему методом введення нових змінних: Позначимо
Зробивши заміну, дістанемо нову систему:
Використаємо метод алгебраїчного додавання, для цього друге рівняння домножимо на (-2) і додамо до першого.
Після виконання додавання отримаємо рівняння з однією змінною Повернемось до попередніх змінних: а друге рівняння на 3 і викоємо додавння.
Звідси 5х=25, х=5 і у=3. Отже коренями системи є (5;3)
Відповідь:(5; 3).
Графічний метод. Щоб розв’язати систему рівнянь із двома змінними графічним способом, потрібно побудувати графіки рівнянь системи в одній системі координат і знайти координати спільних точок цих графіків: ці координати і є розв’язками системи. Але спочатку виконаємо рівносильні перетворення заданої системи так, щоб було зручно будувати графіки всіх рівнянь, що входять до системи. Потім будуємо відповідні графіки і знаходимо координати точок перетину відповідних кривих: ці координати і є розв’язками системи Приклад 5. Розв’яжіть систему
Розв’язування. Обидва рівняння якої є рівняннями другого степеня. Графіком рівняння
Рис.1 Легко перевірити, що координати кожної з цих точок є розв’язком як першого, так і другого рівнянь системи. Тобто, система має 3 розв’язки. Відповідь: (0;5), (-3;-4), (3;-4). Але цей спосіб не є основним способом розв’язування системи рівнянь, тому що він не завжди дає точні результати.
Види систем рівнянь Симетричною системою рівнянь називається система, всі рівняння якої симетричні. Вираз f (x,y) називається симетричним, якщо при заміні х на у, у на х він не змінюється. Приклади симетричних виразів: f(x,y) = х + у; f(x,y) = f(x,y) =
Вирази (x+y) і xy називаються основними симетричнимимногочленами з двома змінними. Усі симетричні вирази з двома змінними виражаються через основні симетричні многочлени, наприклад:
Симетричною системою рівнянь називається система, усі рівняння якої симетричні. Розв’язати симетричну систему можна, наприклад, за допомогою заміни змінних, де новими змінними є основні основні симетричні многочлени.
Приклад 6. Розв’яжіть систему Оскільки
Перша система сукупності має розв’язки (3;5), (5;3); друга система розв’язків не має. Відповідь:(3;5), (5;3). Система двох рівнянь з двома змінними називається однорідною, якщо ліві частини її рівнянь, що містять змінні, є однорідними многочленами степеня п від двох змінних. Таким чином, однорідна система з двома змінними має вигляд
Приклад 7. Розв’яжіть систему Розв’язування. Ліві частини обох рівнянь системи – однорідні многочлени другого степеня від змінних х і у. Якщо в першому рівнянні покласти=0, то дістанемо Однак пара (0;0), що є розв’язком першого рівняння системи, не задовольняє другому рівнянню, тому що
Таким чином, початкова система рівносильна сукупності двох систем рівнянь:
Перша з цих систем має два розв’язки: Друга система несумісна. Звідси (1;2), (-1;-2) – розв’язок початкової системи. Відповідь: (1;2), (-1;-2). ЗАПИТАННЯ І ЗАВДАННЯ ДЛЯ ПОВТОРЕННЯ. 1.Що таке система двох рівнянь з двома змінними? 2.Що називається розв’язком системи двох рівнянь з двома змінними? 3. Що означає розв’язати систему двох рівнянь з двома змінними? 4. Які дві системи рівнянь називаються рівносильними? 5. Назвати основні способи розв’язування систем рівнянь з двома змінними. В чому полягає кожний із способів?
ВПРАВИ. Розв’язати систему рівнянь: Середній рівень
1)
Достатній рівень 5)
Високий рівень 9)
Перевірочна робота ВАРІАНТ 1 Початковий і середній рівні.
1. Укажіть пару рівносильних рівнянь: А)2х - 6=4 і х - 2=4; Б) 3х - 6=0 і 2х=4; В) х2 - 9=0 і х+3=0; Г) х2 - 3х – 4=0 і х+1=0.
2. Яке рівняння не має коренів? А)
3. Укажіть систему, яка відповідає умові задачі: «Число х на 3 менше від числа у, а їхній добуток дорівнює 88. Чому дорівнюють ці числа?». А) 4..Знайдіть множину розв’язків нерівності 3(х - 2) 5. Розв’яжіть рівняння х4 - 8х = 0.
6. Розв’яжіть нерівність | x −1|
Достатній рівень 7. Розв’яжіть рівняння 8. Розв’яжіть систему рівнянь 9. Двоє робітників виготовили за перший день 100 деталей. За другий день перший робітник виготовив деталей на 20 % більше, ніж за перший день, а другий робітник - на 10 % більше, ніж за перший день. Усього за другий день вони виготовили 116 деталей. Скільки деталей виготовив за перший день перший робітник?
Високий рівень У завданні 10 необхідно надати докладні пояснення. 10. Розв’яжіть рівняння
ВАРІАНТ 2 Початковий і середній рівні.
1. Яке рівняння рівносильне рівнянню sin x =2? А) tg x = 2; Б)
2. Яке рівняння не має коренів? А)
3.Укажіть систему рівнянь, яка відповідає умові задачі: «Периметр прямокутника дорівнює 28 дм, а діагональ дорівнює 10 дм. Знайдіть сторони а і b прямокутника». А)
4.Знайдіть множину розв’язків нерівності 2(х + 3)
5. Розв’яжіть рівняння х3 – х2 = 0. 6. Розв’яжіть нерівність | x +2| . Достатній рівень
7. Розв’яжіть рівняння 23х−8∙22х−2х+8=0 8. Розв’яжіть систему рівнянь
9. Знайдіть двозначне число, якщо відомо, що цифра одиниць шуканого числа на 2 більше цифри його десятків і добуток числа на суму його цифр дорівнює 144.
Високий рівень У завданні 10 необхідно надати докладні пояснення. 10 Розв’яжіть рівняння: 6sin2 x − 3sin x cos x − 5cos2 x = 2.
ДОВІДКОВИЙ МАТЕРІАЛ
|
||||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 113; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.14.249.188 (0.009 с.) |

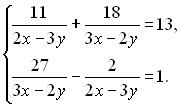
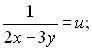
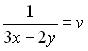 .
.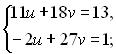
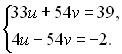
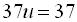
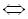
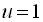 ; Звідси
; Звідси 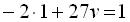
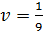
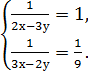
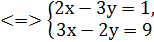
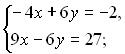
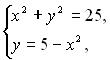
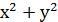 =25 є коло, а графіком рівняння у = 5 -
=25 є коло, а графіком рівняння у = 5 - 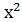 – парабола (рис.1) Ці графіки мають три спільні точки: (0;5), (-3;-4), (3;-4).
– парабола (рис.1) Ці графіки мають три спільні точки: (0;5), (-3;-4), (3;-4).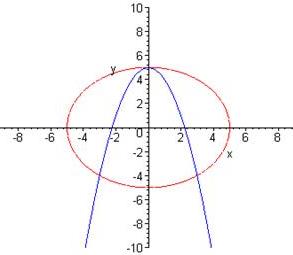
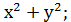 f(x,y) =
f(x,y) = 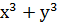
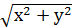 + ху; f(x,y) =
+ ху; f(x,y) = 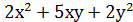 .
.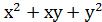 =
= 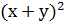 - ху;
- ху; 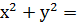
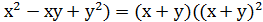 - 3ху) =
- 3ху) = 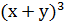 - 3(х + у)ху.
- 3(х + у)ху.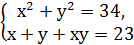
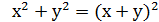 - 2ху, то, поклавши х+у=
- 2ху, то, поклавши х+у= 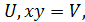 приходимо до такої ситеми:
приходимо до такої ситеми: 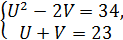 Із цієї системи знаходимо
Із цієї системи знаходимо 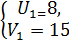 ;
; 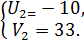 Звідси має сукупність
Звідси має сукупність 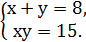 ;
; 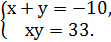
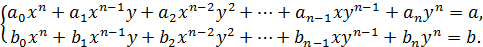
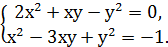
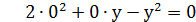
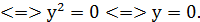
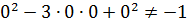 (це не приведе до втрати коренів). Поділивши обидві частини першого рівняння на
(це не приведе до втрати коренів). Поділивши обидві частини першого рівняння на 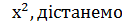
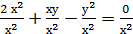
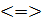 2+
2+ 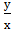 -
- 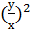 =0
=0 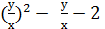 =0. Зробивши заміну
=0. Зробивши заміну 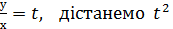 – t - 2= 0
– t - 2= 0 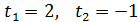 . Тоді
. Тоді 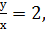 у=2х (х
у=2х (х 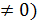 або
або 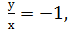 у=-х (х
у=-х (х 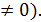
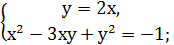
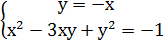
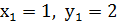 ;
; 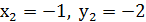
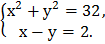 2)
2) 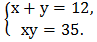 3)
3) 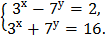 4)
4) 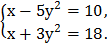
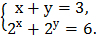 6)
6) 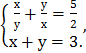 . 7)
. 7) 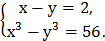 8)
8) 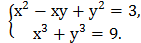
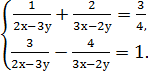 10)
10) 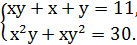 11)
11) 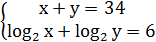
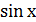 = 2; Б)
= 2; Б) 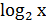 = 1; В) х3 = 2; Г)
= 1; В) х3 = 2; Г) 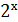 = 1.
= 1.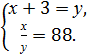 Б)
Б) 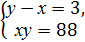 В)
В) 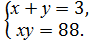 Г)
Г) 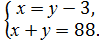
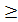 4х – 9.
4х – 9.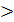 2.
2.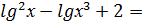 0.
0.
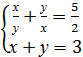
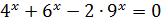
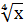 =2; В)2х + 3=2 Г)
=2; В)2х + 3=2 Г) 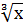 = -2.
= -2.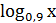 = −1; В) х3 = −0,9; Г)
= −1; В) х3 = −0,9; Г) 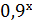 = −1.
= −1.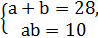 Б)
Б) 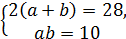 В)
В) 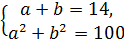 Г)
Г) 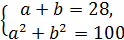
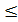 4х +10.
4х +10. 3.
3.