
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ціле раціональне рівняння. Теорема Безу.
Дане рівняння х3 - 5х2 - 2х + 24=0, яке називаєтьсярівнянням степеня вище другого або рівнянням вищого степеня ми розв’язати не можемо, тому що немає знань. Алгебра довгий час розвивалася як наука про розв’язування рівнянь і насамперед рівнянь
Рівняння виду називаються алгебраїчними рівняннями степеня n.
Якщо n =1, то a 0 x + a 1 = 0 - лінійне рівняння. Якщо n = 2, то a 0 x 2 + a 1 x + a 2 = 0 – квадратне рівняння. Якщо n Алгебраїчне рівняння степеня n має не більше n дійсних коренів. Рівняння Рівняння Позначимо Pn(x)= Зауваження. Теорема Безу нерідко формується у такій спосіб: остача від ділення многочлена Рn(х) на двочлен (х - а) дорівнює значенню цього многочлена Рn(х) при х = а, тобто Рn(х)=r, де r- остача від ділення многочлена Рn(х) на двочлен (х - а). Якщо Рn(х) - многочлен з цілими коефіцієнтами, то всякий цілий корінь многочлена Рn(х) є дільником вільного члена an. Якщо нескоротний дріб + an =0, то Тільки у 18 столітті була доведена основна теорема алгебри, про розв’язування рівнянь степеня n, яка була названа в честь французького математика Етьєн Безу. Схема (алгоритм) розв’язування рівнянь вищих степенів, що мають хоча б один цілий корінь: 1) знаходять множину дільників вільного члена an; 2) за теоремою Безу перевіряють, які з цих дільників є розв’язком рівняння Рn(х)=0; 3)діленням у стовпчик знаходять частку від ділення Рn(х) на (х-х1), де х1- корінь рівняння Рn(х)=0; 4) записують частку Qn-1(x) як багаточлен степеня (n-1): Рn(х)= (х-х1)∙ Qn-1(x), де Qn-1(x) многочлен степеня (n-1); 5) визначають, якщо це можливо, корені многочлена Qn-1(x), які також є коренями початкового рівняння.
Приклад 2. Розв’язати рівняннях3 - 5х2 - 2х + 24=0. Розв’язування. Виписуємо дільники вільного члена 24:
Підставляючи у початкове рівняння замість х=-1, дістаємо 20 При х=1 маємо 18 При х=-2, маємо -24+24=0, отже х=-2 є коренем початкового рівняння. За теоремою Безу початковий многочлен без остачі ділиться на (х+2). Виконаємо ділення у стовпчик: _х3 - 5х2 - 2х + 24 х3+2х2 -7 х2 - 2х -7х2 - 14х 12х + 24 12х + 24 0 Таким чином х3 - 5х2 - 2х + 24=(х+2)(х2 - 7х + 12), отже початкове рівняння набуває вигляду (х+2)(х2 - 7х + 12)=0. Це рівняння рівносильне сукупності рівнянь х+2=0 і х2 - 7х + 12=0. Розв’язок першого з яких уже знайдено х= -2. Розв’язуємо друге рівняння х2 - 7х + 12=0, яке має корені х=3 і х=4. Отже початкове рівняння має три корені: х1=-2, х2=3, х3=4. Відповідь:
2) Розв’язування рівняння з однією змінною методом підстановки. Якщо в рівнянні є одинакові вирази зі змінною величиною, які можна замінити новою змінною величиною, то отримаємо більш прості рівняння. Приклад3. Розв’язати рівняння(х2 +3х)2 +2(х2+3х) -120=0. Розв’язування. Якщо х2+3х= у, то отримали зведене квадратне рівняння у2 +2у -120=0; звідси у1= -12 і у2 = 10, тому отримали два рівняння х2+3х=-12 і х2+3х=10. Розв’яжемо їх кожне окремо відносно х. Розв’яжемо перше з них х2+3х=-12, х2 + 3х +12=0, Розв’яжемо друге з них х2 + 3х – 10 = 0, D=49,
Відповідь: -2; 5. 3) Розв’язування рівняння з однією змінною графічним методом. Приклад 4. Розв’язати рівняння Розв’язування. Дане рівняння можна подати у вигляді двох функцій у= Зобразимо на одному малюнку графіки функцій у=
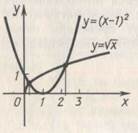
Мал.1
Точкам перетину графіків цих функцій відповідають ті значення аргументу х, при яких співпадають значення функцій, тобто корені даного рівняння. Із малюнку видно, що рівняння має два корені, один із яких знаходиться на інтервалі (0;1), а другий – на інтервалі (2;3), а більш конкретніше х=0,2 і х=2,2 Такий метод розв’язування рівнянь називається графічним. Графічний метод використовують якщо рівняння задано у вигляді: f (x)=g (x). Зображають на одному малюнку графіки функцій у= f (x) і
Графічний метод показує скільки коренів буде мати рівняння та наближено указує проміжки на числовій прямій, де ці корені можуть знаходитись .(приклад 4, мал.1). Якщо рівняння має вид f (x)=0, то в якості функції, яка стоїть у правій частині буде у=0. Графіком її буде вісь х, тому коренями рівняння f (x)=0 будуть абсциси точок перетину графіка функції у= f (x) з віссю х.
|
|||||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 142; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.154.151 (0.012 с.) |
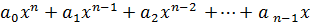 + an = 0 (n
+ an = 0 (n 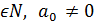 ).
).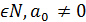 )
)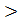 2, то рівняння називається рівнянням степеня вище другого або рівнянням вищого степеня.
2, то рівняння називається рівнянням степеня вище другого або рівнянням вищого степеня.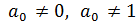 ).
).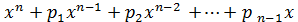 + pn =0 називається зведеним цілим раціональним рівнянням.
+ pn =0 називається зведеним цілим раціональним рівнянням.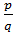 є коренем незведеного цілого раціонального рівняння з цілими коефіцієнтами
є коренем незведеного цілого раціонального рівняння з цілими коефіцієнтами  +
+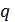 є дільником старшого коефіцієнта а0, а р є дільником вільного члена an.
є дільником старшого коефіцієнта а0, а р є дільником вільного члена an.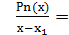 Qn-1(x)
Qn-1(x) 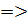
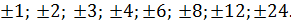
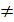 0, отже х=-1 не є коренем початкового рівняння.
0, отже х=-1 не є коренем початкового рівняння.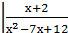
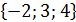
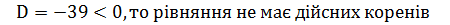
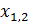 =
= 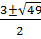 ;
;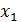 = -2 і
= -2 і 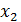 = 5. Отже рівняння (х2 +3х)2 +2(х2+3х) -120=0 має два корені
= 5. Отже рівняння (х2 +3х)2 +2(х2+3х) -120=0 має два корені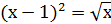 .
.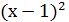 і
і 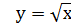 .
.
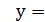 g (x) та знаходимо їх точки перетину.
g (x) та знаходимо їх точки перетину.  Точкам перетину графіків цих функцій відповідають ті значення аргументу х, при яких співпадають значення функцій, тобто корені даного рівняння.
Точкам перетину графіків цих функцій відповідають ті значення аргументу х, при яких співпадають значення функцій, тобто корені даного рівняння.


