Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Однорідні рівняння. Розв’язування однорідних рівнянь методом ділення кожного доданка на Старший степінь.Содержание книги
Поиск на нашем сайте
Однорідні рівняння – це рівняння, в яких кожен з доданків має один і той же степінь. Такі рівняння розв’язуються методом ділення кожного доданка на старший степінь. Приклад 5. Розв’язати рівняння.
Звідси маємо D =
х = 0. Відповідь: х=0. Схема (алгоритм) розв’язування рівнянь з однією змінною: 1) спочатку виконаймо перетворення, використовуючи властивості та формули; 2) використаймо один із методів: розкладання на множники, підстановки (введення нової змінної величини), графічний, ділення кожного доданка на старший степінь; 3) розв’яжемо найпростіші відомі рівняння (лінійне, квадратне, степеневе, показникове, логарифмічне, тригонометричні). Приклад 6. Розв’язати рівняння Розв’язування. Необхідно позбутися від 3 у правій частині, для цього виконаємо перетворення. Подамо
Розділимо на старший степінь
t
D =
tg tg Відповідь:
ЗАПИТАННЯ І ЗАВДАННЯ ДЛЯ ПОВТОРЕННЯ 1.Яку рівність із змінною називають рівнянням? 2. Що означає розв’язати рівняння з однією змінною? 3. Що називається коренем рівняння з однією змінною? 4.Сформулювати основні властивості рівнянь та наслідок з них. 5.Які два рівняння називаються рівносильними? 6.Які основні види рівнянь з однією змінною ви знаєте? 7. Скільки коренів має лінійне рівняння? 8. Скільки коренів має квадратне рівняння? 9. Скільки коренів має просте степеневе рівняння при різних n і а (n- натуральне число)? 10. Скільки коренів має просте показникове рівняння при різних а і b? 11. При яких значеннях а тригонометричні рівняння sinx=a та cosx=a не мають розв’язків 12. Які етапи (кроки) необхідно виконати, щоб розв’язати рівняння з однією змінною. 13. Назвати основні методи розв’язування рівнянь з однією змінною. 14. Як розкласти многочлен на множники способом групування? 15. Сформулюйте теорему Безу. 16.Коли застосовують метод підстановки (введення нової змінної)? 17. В чому полягає метод розкладання на множники.
18. В чому полягає графічний метод. ВПРАВИ Початковий та середній рівень. 1.Які рівняння рівносильні: sin x =2; tg x = 2; 2х - 6=4; х - 2=4; 3х - 6=0; 2х=4; х2 - 9=0 х+3=0; х2 - 3х – 4=0 х+1=0.
2. Яке рівняння не має коренів:
3. Розв’яжіть рівняння: 1) 5х+4=0; 2) 3) 2х2+5х-3=0; 4) х4 - 8х = 0; 5)х3 – х2 = 0; 6) Достатній рівень
7) log32x - 4log3x+3=0; 8) 9) х3+3х2+5х+3=0; 10) cos2 x - 3sinx 11)23х−8∙22х−2х+8=0; 12) sin2x+ Високий рівень 13) Розв’яжіть рівняння 14) 9 15) 2 16) sinx+sin2x+sin3x = 0; 17) 6sin2 x − 3sin x cos x − 5cos2 x = 2.
САМОСТІЙНА РОБОТА №1 Варіант -1
Розв’язати рівняння
6б 1. х2 – 2х- 8=0; 2. х3 +16х=0;
9б 3. 33х−9∙32х−3х+9=0; 4.
10-11б 5. х3+3х2 +5х+3=0. 6.6sin2 x − 3sin x cos x − 5cos2 x = 2.
Варіант-2
Розв’язати рівняння
6б 1. х2 – 6х + 8=0; 2. х4 - 16х2 =0;
9б 3. 4.
10-11б 5. х3+3х2 +5х+3=0. 6.
Тема. РОЗВ’ЯЗУВАННЯ ЗАДАЧ, ЯКІ ЗВОДЯТЬСЯ ДО РІВНЯНЬ
|
|||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 126; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.241.104 (0.01 с.) |

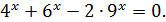 Розв’язування. Всі доданки мають один і той же степінь. Виконаємо перетворення
Розв’язування. Всі доданки мають один і той же степінь. Виконаємо перетворення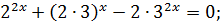
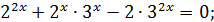 Старший степінь 2х, то кожний доданок розділимо на
Старший степінь 2х, то кожний доданок розділимо на 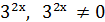
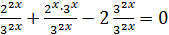 тоді
тоді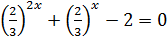 Введемо підстановку. Нехай
Введемо підстановку. Нехай 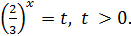
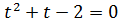
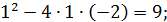
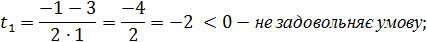
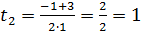 , тому
, тому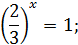
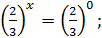 отже
отже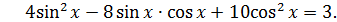
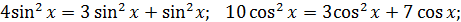
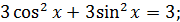 тоді початкове рівняння буде мати вид:
тоді початкове рівняння буде мати вид: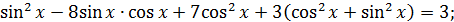
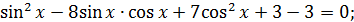
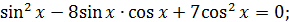
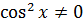
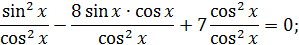
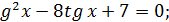 Вводимо підстановку
Вводимо підстановку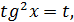 t
t 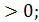
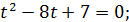
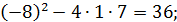
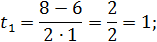
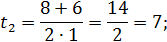
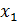 = 1;
= 1; 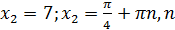 ∈ N.
∈ N.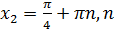 ∈N
∈N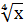 =2; 2х + 3=2;
=2; 2х + 3=2; 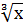 = -2;
= -2;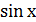 = 0,9;
= 0,9; 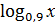 = −1; х3 = −0,9;
= −1; х3 = −0,9; 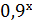 = −1; sin x =2
= −1; sin x =2 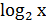 = 1; х3 = 2;
= 1; х3 = 2; 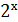 = 1.
= 1.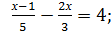
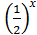 =3+х.
=3+х.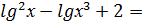 0;
0;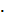 cosx +1= 0;
cosx +1= 0;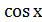 =0;
=0;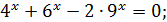
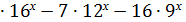 = 0;
= 0;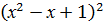 = 5
= 5 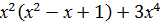 ;
;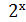 =2+х;
=2+х;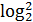 x+
x+ 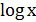 -2=0;
-2=0;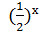 =3 - х;
=3 - х;