Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: Археология Биология Генетика География Информатика История Логика Маркетинг Математика Менеджмент Механика Педагогика Религия Социология Технологии Физика Философия Финансы Химия Экология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления	Главная Избранные Случайная статья Познавательные Новые добавления Обратная связь FAQ Решение дифференциальных уравнений ⇐ ПредыдущаяСтр 4 из 4 для нахождения Vym (t) и Δ ym (t): Приведем исходное значение дифференциального уравнения 2-го порядка к системе двух дифференциальных уравнений 1-го порядка в канонической форме (то есть в левых частях этих уравнений должны быть только первые производные от неизвестных функций ∆ym(t) и Vym(t)). 1-е дифф. уравнение получим из определения скорости тела: d/dt∆ym(t)= Vym(t)                             (1) 2-eдифф. уравнение получим из принципа Даламбера: d/dtVym(t)=(1/m)*[Cd*(Vys(t) –Vym(t))+Kpr* (∆ys(t) – ∆ym(t))]   при нулевых начальных условиях (∆ym(0)=0 и Vym(0)=0). Начальные условия: ∆ym(0)=0; Vym(0)=0   Решим систему дифф. уравнений        d/dt∆ym(t)= Vym(t) d/dtVym(t)=(1/m)*[Cd*(Vys(t)- Vym(t))+Kpr* (∆ys(t) – ∆ym(t))]   Подставив 1-е дифф. уравнение во 2-е и получим:   d/dtVym(t)=(1/m)*[Cd*(Vys(t) –d/dt∆ym(t))+Kpr* (∆ys(t) – ∆ym(t)) следовательно   Vym(t)=∫0-2*Ts (1/m)*[Cd*(Vys(t)–d/dt∆ym(t))+Kpr* (∆ys(t)– ∆ym(t))dt     из приложения MathCAD Результат решения системы двух дифференциальных уравнений: Таблица 7из приложения Excel № t Ym(t)	Vym(t)	№	t	ym(t)	Vym(t)
1	0	0	0	3 1	1	-0,242	-0,526
2	0,033333	-3,46E-04	-0,017	3 2	1,033333	-0,26	-0,552
3	0,066667	-8,73E-04	-0,012	3 3	1,066667	-0,279	-0,585
4	0,1	-9,71E-04	7,89E-03	3 4	1,1	-0,299	-0,614
5	0,133333	-2,52E-04	0,036	3 5	1,133333	-0,32	-0,628
6	0,166667	1,46E-03	0,066	3 6	1,166667	-0,341	-0,614
7	0,2	4,13E-03	0,093	3 7	1,2	-0,36	-0,565
8	0,233333	7,52E-03	0,109	3 8	1,233333	-0,378	-0,483
9	0,266667	0,011	0,111	3 9	1,266667	-0,392	-0,373
10	0,3	0,015	0,097	40	1,3	-0,403	-0,242
1 1	0,333333	0,018	0,066	4 1	1,333333	-0,408	-0,1
1 2	0,366667	0,019	0,02	4 2	1,366667	-0,409	0,045
1 3	0,4	0,019	-0,039	4 3	1,4	-0,405	0,187
1 4	0,433333	0,016	-0,106	4 4	1,433333	-0,397	0,318
1 5	0,466667	0,012	-0,178	4 5	1,466667	-0,384	0,436
1 6	0,5	4,44E-03	-0,249	4 6	1,5	-0,368	0,535
1 7	0,533333	-5,03E-03	-0,318	4 7	1,533333	-0,349	0,615
18	0,566667	-0,017	-0,381	48	1,566667	-0,327	0,674
19	0,6	-0,03	-0,436	49	1,6	-0,304	0,712
20	0,633333	-0,046	-0,482	50	1,633333	-0,28	0,731
21	0,666667	-0,062	-0,518	51	1,666667	-0,256	0,732
22	0,7	-0,08	-0,543	52	1,7	-0,231	0,717
23	0,733333	-0,098	-0,559	53	1,733333	-0,208	0,691
24	0,766667	-0,117	-0,565	54	1,766667	-0,186	0,656
25	0,8	-0,136	-0,563	55	1,8	-0,164	0,617
26	0,833333	-0,155	-0,553	56	1,833333	-0,144	0,578
27	0,866667	-0,173	-0,54	57	1,866667	-0,126	0,543
28	0,9	-0,191	-0,525	58	1,9	-0,108	0,515
29	0,933333	-0,208	-0,514	59	1,933333	-0,091	0,494
30	0,966667	-0,225	-0,514	60	1,966667	-0,075	0,479
				61	2	-0,059	0,469

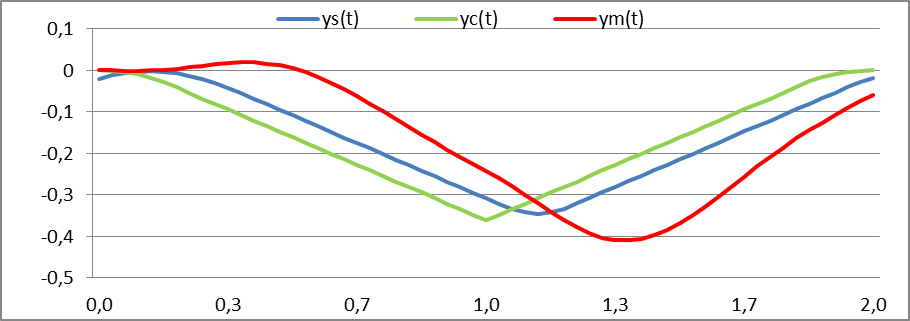
Рис. 8. Относительные высоты:

(1) массивного тела Δym (t) [мм](красная линия)

(2) оси упругого колеса Δys (t) [мм] (синяя линия)                                                         (3) оси жесткого колеса Δyc (t) [мм] (зеленая линия)

из приложения MathCAD

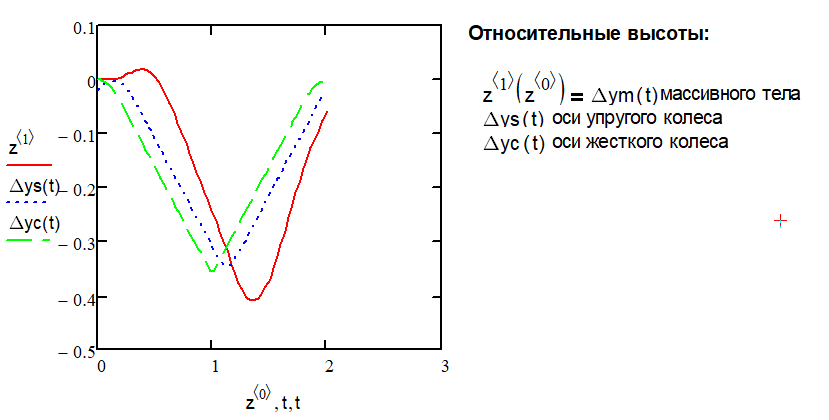
Вывод. Из этих графиков видим следующее:

1. Зависимость относительной высоты Δ ym (t) массивного тела имеет более плавный и более протяженный характер.

2. Амплитуда функции Δ ym (t) массивного тела также значительно превышает амплитуды функций Δ yc (t) и Δ ys (t).

3. График Δ ys (t) очевидно более плавный,чем Δ yc (t), что связано с плавным перетеканием вязкой жидкости

из приложения Excel

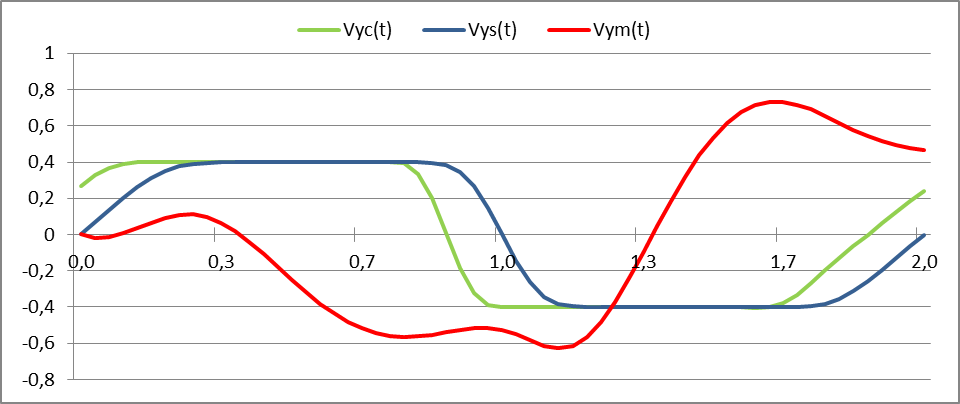
Рис. 9. Относительные скорости:

1) массивного тела Vym (t) [мм](красная линия)

2) оси упругого колеса Vys (t) [мм] (синяя линия)

3) оси жесткого колеса Vyc (t) [мм] (зеленая линия).

из приложения MathCAD

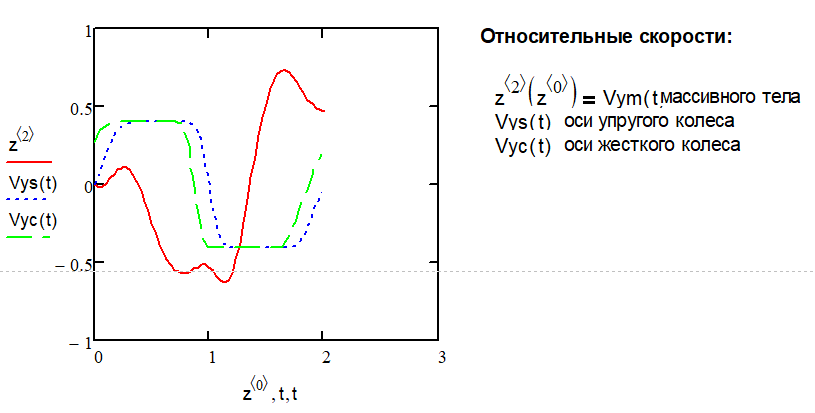
Вывод. Из этих графиков видим следующее. Зависимость Vym (t) вертикальной скорости массивного тела имеет более плавный и более протяженный характер, чем зависимость Vys (t) вертикальной скорости сглаженной высоты центра упругого колеса.

 

из приложения MathCAD

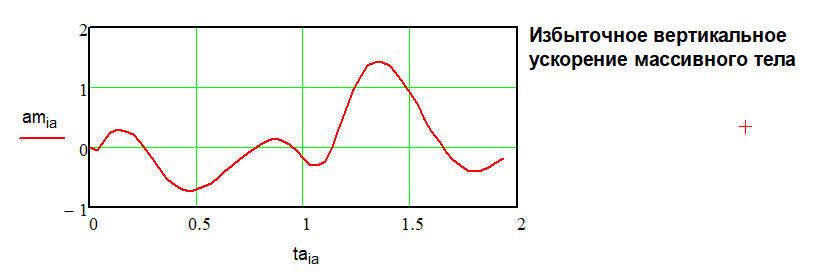
Рис. 10. Избыточное вертикальное ускорение массивного тела

 

 

Этап 3

Исследование зависимости избыточного ускорения

Массивного тела от одного из параметров системы

из приложения MathCAD

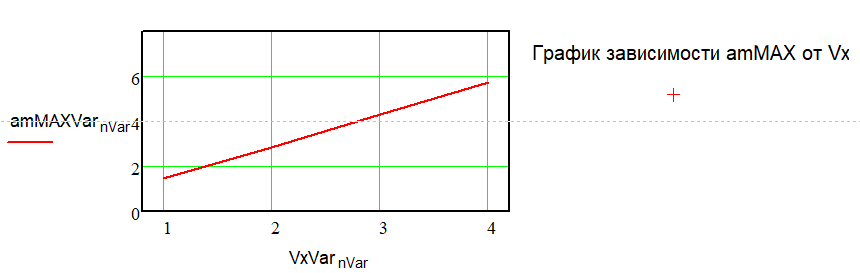
Рис.11. График зависимости amMAX от Vx.

Аппроксимация функции полиномом второй степени

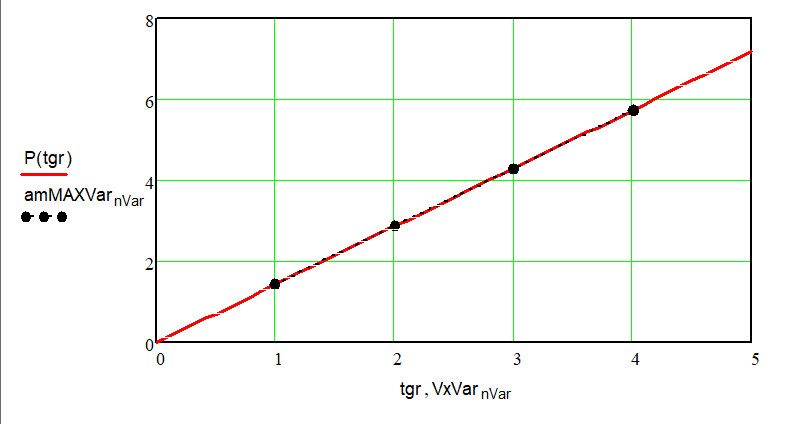
Рис.12. График зависимости amMAX от Vx и

кривая аппроксимирующего полинома.

Вывод. Из графика видно, что амплитуда ускорения массивного тела зависит практически линейно от горизонтальной скорости колеса.

Заключение

 

Применение численных методов сводится к замене математических операций и отношений соответствующими операциями над числами, например, к замене интегралов суммами, бесконечных сумм – конечными и т.п. Результатом применения численных методов являются таблицы и графики зависимостей, раскрывающих свойства объекта. Численные методы являются продолжением аналитических методов в тех случаях, когда результат не может быть получен в явном виде. Численные методы по сравнению с аналитическими методами позволяют решать значительно более широкий круг задач.

Предложенные преподавателем программы показали себя эффективно для решения конкретных задач, под которые они были написаны. Но их использование для решения различных инженерных задач нецелесообразно из-за крайне ограниченного функционала. Возможный выход – это самостоятельное написание программ под конкретные задачи, но это чревато большими трудозатрами. Альтернатива – использование коммерческих пакетов (например, системы математического моделирования MathCAD, Excel и т.д.), позволяющих решать очень широкий круг задач.

С использованием этих программ, была создана корректная модель движения жёсткого колеса и установлено, что при преодолении препятствия происходит сглаживание острых углов препятствия. Применив параметр эффективного сглаживания упругого колеса установлено, что при спуске происходит запаздывания, а при подъёме опережение траектории жесткого колеса, кроме того еще сильнее проявляется эффект сглаживания острых углов препятствия.

Выяснено, что из-за значительной скорости колеса необходимо учитывать амортизацию.

Учитывая такие параметры как: масса тела, упругость пружины и коэффициент демпфирования стало ясно, что происходит сглаживание и растягивание траектории, увеличивается амплитуда колебаний.

Найдена линейная зависимость амплитуды ускорения массивного тела от горизонтальной скорости колеса.