
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Нижегородский государственный техническийСодержание книги
Поиск на нашем сайте Нижегородский государственный технический университет им. Р.Е. Алексеева
КУРСОВАЯ РАБОТА по дисциплине «Информатика»
Тема: Численное и графическое моделирование и исследование кинематических и динамических характеристик механической системы
вариант 27 Руководитель Балакина Н.А. (подпись) (фамилия, и.,о.) « » 2019г. (дата) Студент Каночкин М.М. (фамилия, и.,о.) А18-ЭТКз (подпись) (группа) «» __________________2019г. (дата) Работа защищена « » 2019г. c оценкой Зачетная книжка № _________
Н. Новгород 2019 г.
Содержание Введение 1.Постановка задачи 2. Модели механической системы 2.1Физическая модель системы 2.2 Процесс работы и силы, возникающие в системе 2.3 Упрощенная физическая модель всей системы 2.4 Упрощенные физическая и геометрическая модели упругогоколеса 2.5 Физические законы, описывающие процессы в системе 2.6 Математическая модель задачи 3. Этапы выполнения курсовой работы 3.1 Этап 1. Расчет координат центра упругого колеса и скорости их изменения по участкам траектории центра жесткого колеса 3.2 Этап 2. Расчет динамических характеристик механической системы 3.3 Этап 3. Исследование зависимости избыточного ускорения массивного тела от одного из параметров системы Введение В курсе «Информатика» изучались следующие разделы: 1. Принципы алгоритмизации и программирования. 2. Элементы численных методов, используемых в инженерных расчетах. 3. Работа пользователя в программных средах MicrosoftOffice, MathCAD, Excel и др. на примерах реализации численных методов. 4. Оформление результатов расчетов в указанных программных продуктах, в редакторе MicrosoftOffice, 3D-САПР AutodeskInventor и др. В данной курсовой работе на примере упрощенной инженерной задачи о механической системе применены знания, полученные при изучении указанных разделов и умение их применить в конкретных задачах. Задача, поставленная в данной курсовой работе, не требует каких-либо специальных знаний, кроме уже изученных в курсе физики (законов механики) в математическом анализе: 1. элементарные теоремы геометрии для треугольников и окружностей; 2. законы механики Ньютона; 3. закон Гука для упругой пружины; 4. закон сопротивления движению в вязких жидкостях; 5. сведения о простейших дифференциальных уравнениях. Постановка задачи В данной работе рассматривается задача расчета и исследования кинематических идинамических характеристик механической системы, схема которойизображена на рисунке 1.
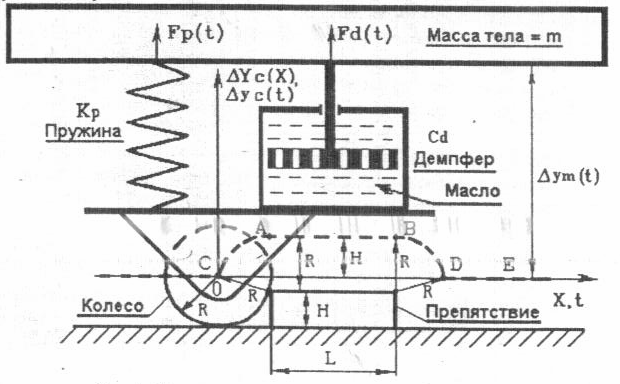
Рис. 1. Кинематическая схема механической системы и траектория центра жесткого колеса Система содержит: - массивное жесткое тело массой m; - жесткую опору и жесткое неподвижное препятствие; - упругое колесо радиусом R; - пружинно-демпферный амортизатор, состоящий из параллельно соединенных пружины и демпфера; амортизатор жестко соединен с массивным телом и шарнирно соединен с колесом. Основные допущения: 1. Массы всех частей амортизатора и колеса значительно меньше массы массивного тела, поэтому их массами можно пренебречь. 2. Вся система перемещается по горизонтали с малой постоянной скоростью, а по вертикали – с переменной скоростью без вращения вокруг любых точек или осей за счет дополнительных связей, не изображённых на рисунке 1. 3. При малой горизонтальной скорости V х и достаточно большой массе тела т колесо постоянно соприкасается с опорой и/или с препятствием (то есть колесо не подпрыгивает и не летит по воздуху). 4. Начало декартовой системы координат расположим в центре жесткого колеса (в точке С) при первом соприкосновении колеса с препятствием. 5. Изменение реакции пружины Δ Fpr (l) линейно зависит от изменения ее длины Δ Lpr (t). 6. Реакция демпфера Fd (t) линейно зависит от скорости перемещения поршня относительно корпуса демпфера. Модели механической системы Физическая модель системы Физической моделью системы называется качественное описание явлений, происходящих при функционировании того или иного механизма, прибора или другого изделия.Физической модели соответствуют: 1. рисунки, эскизы, чертежи, схемы изделия; 2. перечень физических явлений, законов, соответствующих процессу функционирования изделия; 3. описание процесса функционирования изделия, а также физических величин (координаты, скорости, ускорения, силы и др.). Этап 1 3.1 Расчет координат центра упругого колеса и скорости их изменения по участкам траектории центра жесткого колеса Исходные данные для расчета кинематических характеристик системы: R=0.33 Радиус колеса, [м]; H=0.4 Высота препятствия, [м]; L=4*H; L=1.6 Длина препятствия, [м]; Vx=0.8 Горизонтальная скорость системы, [м/с]; cLs=0.4; Ls=cLs*R; Ls=0.132 Длина сцепления колеса с опорой, [м]; Ts=Ls; Ts=0.132Эффективное время сглаживания траектории центра жесткого колеса, [с]; Xk=1.6 Конечное значение продольной координаты по умолчанию [м] tk=Xk/Vxtk=2 Конечное значение времени наблюдения [с] при расчете кинематики системы Шаг 1. 1. Расчет координаты точек из приложения AutodeskInventor
Рис. 2. Эскиз ожидаемой траектории центра жесткого колеса 1.1.1 Расчет точки координат
Таким образом, координаты точки
1.1.2 Расчет точки координат
Таким образом, координаты точки
1.1.3 Расчет точки координат
Таким образом, координаты точки
1.1.4 Расчет точки координат
Таким образом, координаты точки Шаг 1. 2. Расчет уравненийтраектории ∆ Y (x) участков
1.2.1 Расчет уравнения траектории 1-го участка
Вывод: т.к. результаты расчетов ∆Y(x) на границах 1-го участка совпадают с заданными, а в центре участка значение ∆Y(x)совпадает с чертежом, то функция ∆Y(x) найдена верно. 1.2.2 Расчет уравнения траектории 1-го участка Используя метод линейной интерполяции
Вывод: т.к. результаты расчетов ∆Y(x) на границах 2-го участка совпадают с заданными, а в центре участка значение ∆Y(x)совпадает с чертежом, то функция ∆Y(x) найдена верно. 1.2.3 Расчет уравнения траектории 1-го участка Используя метод линейной интерполяции
Вывод: т.к. результаты расчетов ∆Y(x) на границах 3-го участка совпадают с заданными, а в центре участка значение ∆Y(x)совпадает с чертежом, то функция ∆Y(x) найдена верно. 1.2.1 Расчет уравнения траектории 1-го участка
Вывод: т.к. результаты расчетов ∆Y(x) на границах 1-го участка совпадают с заданными, а в центре участка значение ∆Y(x) совпадает с чертежом, то функция ∆Y(x) найдена верно.
С помощью полученных уравнений (шаг 1.2)траектории движения центра жесткого колеса научастках Таблица 1 Значения координат перемещения центра жесткого колеса
Рис. 2. Траектория движения центра жесткого колеса Вывод. Из графика траектории движения жесткого колеса видно: 1. Траектория более сглаженная и плавная, чем само препятствие. 2. График траектории движения жесткого колеса соответствует реальной траектории движения жесткого колеса. 3. При преодолении препятствия жестким колесом происходит сглаживание острых углов препятствия.
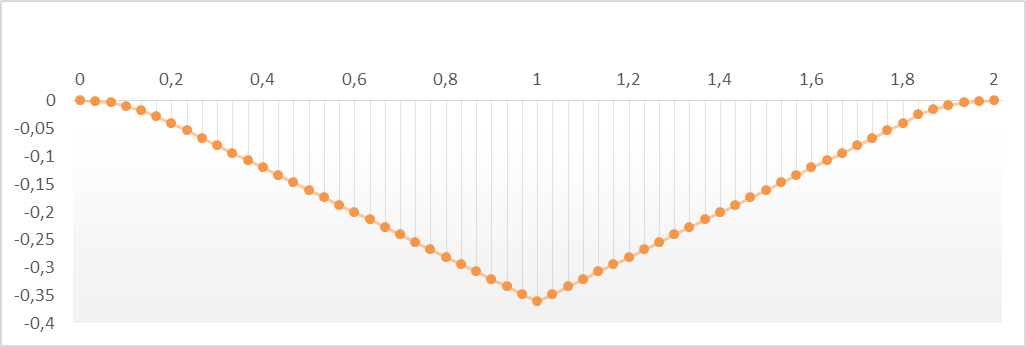
Шаг 1. 2. Расчет зависимости от времени высоты центра жесткого колеса ∆ yc (t). Функция зависимости от времени высоты [м] оси жесткого колеса при любом времени t: ∆yc(t)= ∆Yc(t*Vx) tn=0(начальное значение времениt) tk= 2 (конечное значение времениt) ht=(tk-tn)/60 (шаг времениt) ht=0.033333333 tc = tn, ht..tk С помощью выведенных (шаг 1.1) уравнений траектории движения центра жесткого колеса на участках A-B, B-Cи C-D и формулы зависимости от времени высоты оси жесткого колеса ∆yc(t)= ∆Yc(t*Vx) при любом времени t составим таблицу в MicrosoftExcel и получим графическое изображение зависимости высоты центра жесткого колеса от времени.
Таблица 2 Значения высоты центра жесткого колеса от времени
Рис 3. Зависимость высоты центра жесткого колеса от времени Вывод. из графика зависимость высоты центра жесткого колеса от времени видно: 1. Траектория более растянута по сравнению с траекторией Рис2. Шаг 1. 3. Расчет траектории центра упругого колеса ∆ ys (t) График функции Wys(τ),сглаживающей зависимости от времени∆yc(t) – высоты центра упругого колеса (–2*Ts ≤ τ ≤ 0): ПРОВЕРКА нормировки Wys(τ) (вручную)
Наши данные: Ts=0,132 (эффективное время сглаживания траектории упругими колесами)
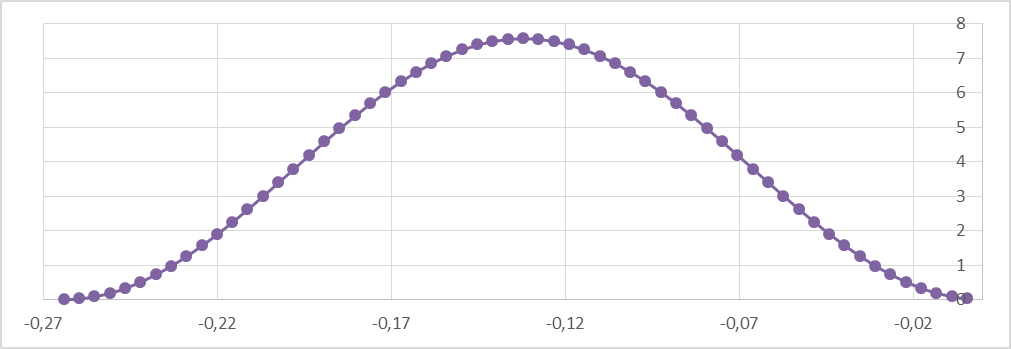
hτ=Ts/60 hτ=0,0022τn= – 2*TSτn= –0,264 τk=0 τ=τn, τn+hτ.. τk Cоставим таблицу в MicrosoftExcel и получим графическое изображение сглаживающей функцииWys(τ). Таблица 3 Значения сглаживающей функции
Рис. 4.Сглаживающая весовая функцияW ys (τ) Вывод. На графике видно, что функция Wys(τ) действительно является сглаживающей (сглаживает зависимость высоты центра упругого колеса от времени) Ts – эффективное время сглаживания траектории упругими колесами). Вывод. 1. Сглаживание графика функции Vys(t) действительно происходит благодаря амортизации. 2. Амортизация необходима из-за значительных величин скоростей жесткого колеса. 3. Скорость Этап 2 Механической системы Согласно принятым допущениям при малых изменениях длины пружины Δ Lpr (t) реакция пружины ( Δ Fpr) находится по линейному закону Гука: Δ Fpr (t)= Kpr Δ Lpr (t)= Kpr [ Δ ys (t)- Δ ym (t)]. Здесь Кр r – коэффициент восстанавливающей силы упругой пружины; Δ ys (t) – ранее найденная временная зависимость относительной высоты оси упругого колеса. Δ ym (t) = ym (t)- ym (0) – изменение начальной высоты массивного тела относительно назальной высоты ym (0) массивного тела при t =0. При малых значениях Vd – скорости перемещения поршня силу Δ Fd (t) будем находить по линейному закону для силы сопротивления жидкого трения: Δ Fd (t) = – CdVd { t)= – Cd [ Vym (t) – Vys { t)] В этой формуле знак силы Δ Fd (t) противоположен Vd (t) – скорости изменения расстояния от поршня до дна корпуса демпфера. Здесь также обозначено: Vym (t) = d / dt [ Δ ym (t)] и Vys (t) = d / dt [ Δ ys (t)] – скорости изменения вертикальной координаты массивного тела и центра колеса. Из физических соображений найдем систему, двух дифференциальных уравнений относительно двух неизвестных функций Δ ym (t) и Vym (t): 1-е дифференциальное уравнение относительно Δ ym (t) и Vym получим из определения скорости тела: d / dt [ Δ ym (t)] = Vym (t) (1) 2-е дифференциальное уравнение получим из 2-го закона Ньютона. Произведение массы тела т на его ускорение d / dt [ Vym (t)] равно алгебраической сумме всех внешних сил, действующих на это тело. d / dt [ Vym (t)]=(1/ m){ Kpr [ Δ ys (t)- Δ ym (t)]+ Cd [ Vys (t)- Vym (t)] (2)
Согласно принципу Даламбера, любое движущееся массивное тело находится в состоянии динамического (силового) равновесия, если сила инерции тела равна сумме всех внешних сил, действующих на это тело: ∆Fm(t)= ∆Fpr(t)+Fd(t), где ∆Fm(t) – сила инерции массивного тела, вычисляемая по2-му закону Ньютона: ∆Fm(t)=m*(d/dtVym(t)); Vym(t) –вертикальная составляющая скорости тела; ∆Fpr(t)Kpr*[∆ys(t) –∆ym(t)] – избыточная сила сжатия пружины (закон Гука); Fd(t)=Cd*[Vys(t) –Vym(t)] – сила сопротивления движению поршня в жидкости демпфера. Неизвестные функции ∆ym(t) иVym(t)=d/dt∆ym(t)находятся из дифференциального уравнения 2-го порядка: M*(d2/dt2∆ym(t))=Cd*(Vys(t) – d/dt∆ym(t))+Kpr*(∆ys(t) –∆ym(t))
Исходные данные необходимые для расчета динамических характеристик системы(подготовка данных для решения дифференциального уравнения) m =300 Масса тела по умолчанию m=300[кг] X С =1,6 Конечная продольная координата препятствия [м] Tprep =XС/Vx Tprep =2Время прохождения препятствия колесом [с] Tkoleb =1 Период собственных колебаний системы (Tkoleb) cTau =0,45 Отношение постоянной времени затухания колебаний (Tau) к периоду собственных колебаний (Tkoleb) (Tau<Tkoleb). Tau =cTau* Tkoleb Tau =0,45 Постоянная времени затухания колебаний [с] Расчет коэффициента демпфирования Cd: Cd=2m/Tau Cd=1333,33 [H*с/м] Расчет коэффициента упругости пружины Kpr: Kpr =m*[(2π/ Tkoleb)2+(1/Tau)2] Kpr=13333,33 [H/м] Собственные колебания массивного тела fcos 0(t)= e - t / Tau * cos (2 πt / Tkoleb) – реакция системы на единичное вертикальное смещение массивного тела на [1м] fsin 0(t)= e - t / Tau * sin (2 πt / Tkoleb) –реакция системы на единичную вертикальную скорость массивного тела [1м/c] Tkoleb=1 Период собственных колебаний [с]
[c] t=tn, ht..2* Tkoleb t=0,0.004..2 Tprep=2 Время прохождения препятствия колесом [с] Nt =60 Число расчетных шагов по времени tn =0 Начальное значение времени t tk =2 Конечное значение времени t шаг по времени: ht=(tk-tn)/Nt; ht=0,004 С помощью данных уравнений функций fcos 0(t) и fsin 0(t) при t=0,0.004..2составим таблицу зависимостей функций fcos 0(t) и fsin 0(t) от времени t вMicrosoftExcel. С помощью полученных данных таблицы построить графики функций зависимости fcos 0(t) и fsin 0(t) от времени t.
Таблица 6 Значения функций собственных колебаний массивного тела
Fcos0(t) | 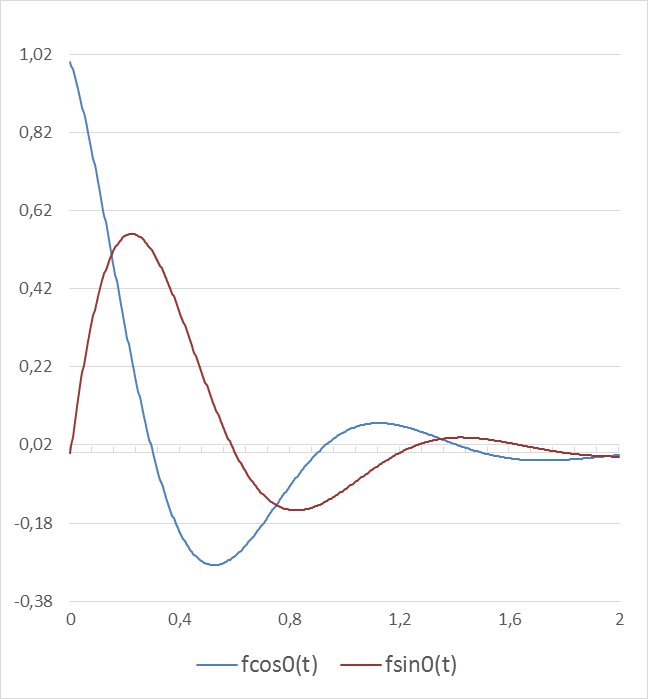 fsin0(t) fsin0(t)
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1 | 0 | 1 | 0 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2 | 0,033333 | 0,914495 | 0,16125 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3 | 0,066667 | 0,8103 | 0,294925 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4 | 0,1 | 0,693459 | 0,400369 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 5 | 0,133333 | 0,569605 | 0,477956 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6 | 0,166667 | 0,443831 | 0,528937 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7 | 0,2 | 0,32059 | 0,555279 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 8 | 0,233333 | 0,203639 | 0,559495 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 9 | 0,266667 | 0,096009 | 0,544492 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 10 | 0,3 | 3,15E-17 | 0,513417 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
5 7 | 1,866667 | -0,01484 | -0,0054 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
5 8 | 1,9 | -0,0127 | -0,00733 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
5 9 | 1,933333 | -0,01043 | -0,00875 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
6 0 | 1,966667 | -0,00813 | -0,00969 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
6 1 | 2 | -0,00587 | -0,01017 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Рис 7.2 График собственных колебаний
массивного тела, полученный в приложении Excel
из приложения MathCAD


Рис 7.1 График собственных колебаний массивного тела, полученный в приложении MathCAD
Ym(t)
Vym(t)
0
0
0
0,033333
-3,46E-04
-0,017
0,066667
-8,73E-04
-0,012
0,1
-9,71E-04
7,89E-03
0,133333
-2,52E-04
0,036
0,166667
1,46E-03
0,066
0,2
4,13E-03
0,093
0,233333
7,52E-03
0,109
0,266667
0,011
0,111
0,3
0,015
0,097
0,333333
0,018
0,066
0,366667
0,019
0,02
0,4
0,019
-0,039
0,433333
0,016
-0,106
0,466667
0,012
-0,178
0,5
4,44E-03
-0,249
0,533333
-5,03E-03
-0,318
0,566667
-0,017
-0,381
0,6
-0,03
-0,436
0,633333
-0,046
-0,482
0,666667
-0,062
-0,518
0,7
-0,08
-0,543
0,733333
-0,098
-0,559
0,766667
-0,117
-0,565
0,8
-0,136
-0,563
0,833333
-0,155
-0,553
0,866667
-0,173
-0,54
0,9
-0,191
-0,525
0,933333
-0,208
-0,514
0,966667
-0,225
-0,514
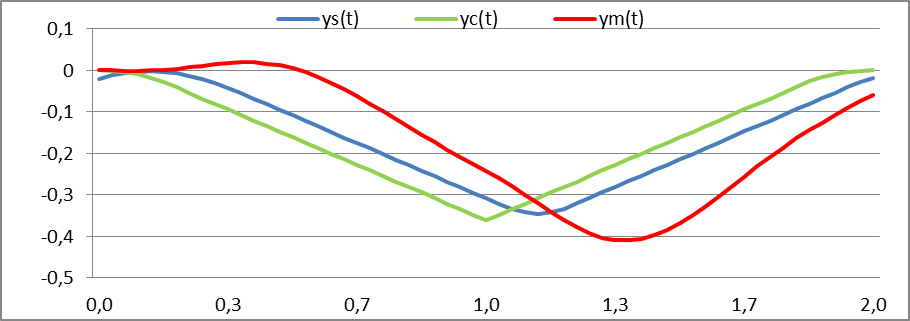
Рис. 8. Относительные высоты:
(1) массивного тела Δym (t) [мм](красная линия)
(2) оси упругого колеса Δys (t) [мм] (синяя линия) (3) оси жесткого колеса Δyc (t) [мм] (зеленая линия)
из приложения MathCAD
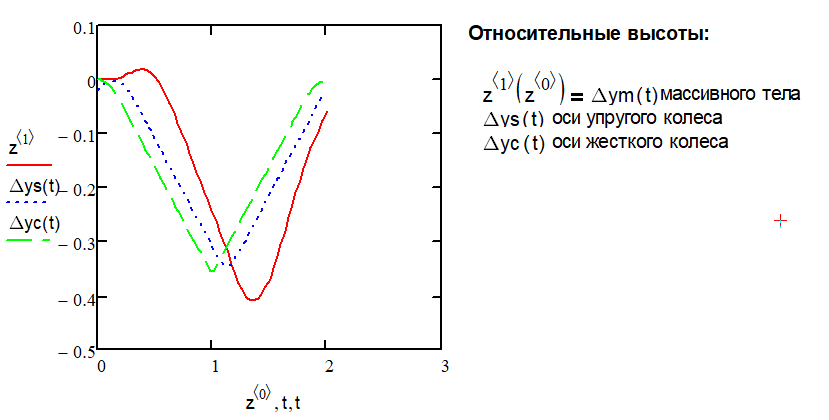
Вывод. Из этих графиков видим следующее:
1. Зависимость относительной высоты Δ ym (t) массивного тела имеет более плавный и более протяженный характер.
2. Амплитуда функции Δ ym (t) массивного тела также значительно превышает амплитуды функций Δ yc (t) и Δ ys (t).
3. График Δ ys (t) очевидно более плавный,чем Δ yc (t), что связано с плавным перетеканием вязкой жидкости
из приложения Excel
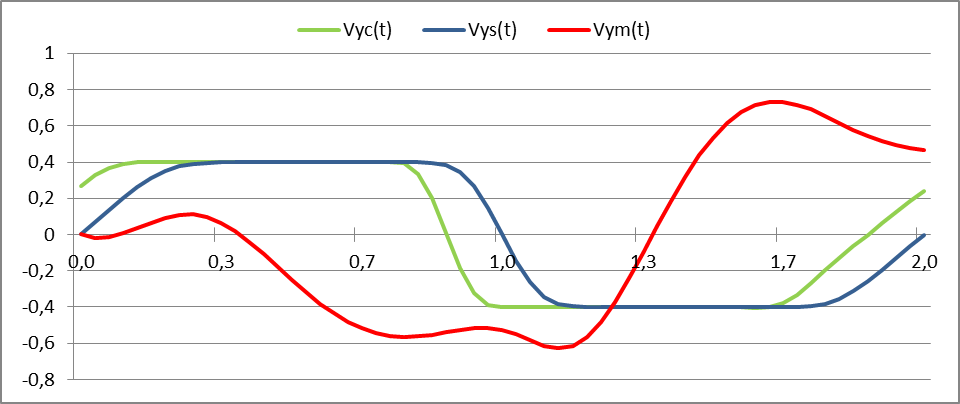
Рис. 9. Относительные скорости:
1) массивного тела Vym (t) [мм](красная линия)
2) оси упругого колеса Vys (t) [мм] (синяя линия)
3) оси жесткого колеса Vyc (t) [мм] (зеленая линия).
из приложения MathCAD
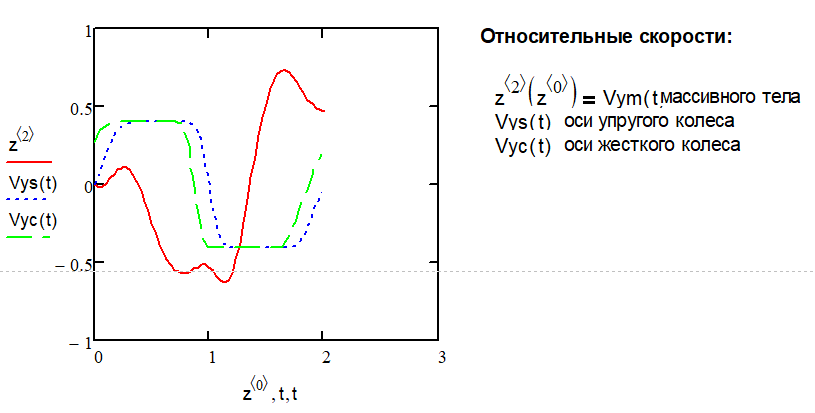
Вывод. Из этих графиков видим следующее. Зависимость Vym (t) вертикальной скорости массивного тела имеет более плавный и более протяженный характер, чем зависимость Vys (t) вертикальной скорости сглаженной высоты центра упругого колеса.
из приложения MathCAD<
|
| Поделиться: |

 (центра жесткого колеса) при преодолении препятствия относительно его положения при соприкосновении колеса с препятствием
(центра жесткого колеса) при преодолении препятствия относительно его положения при соприкосновении колеса с препятствием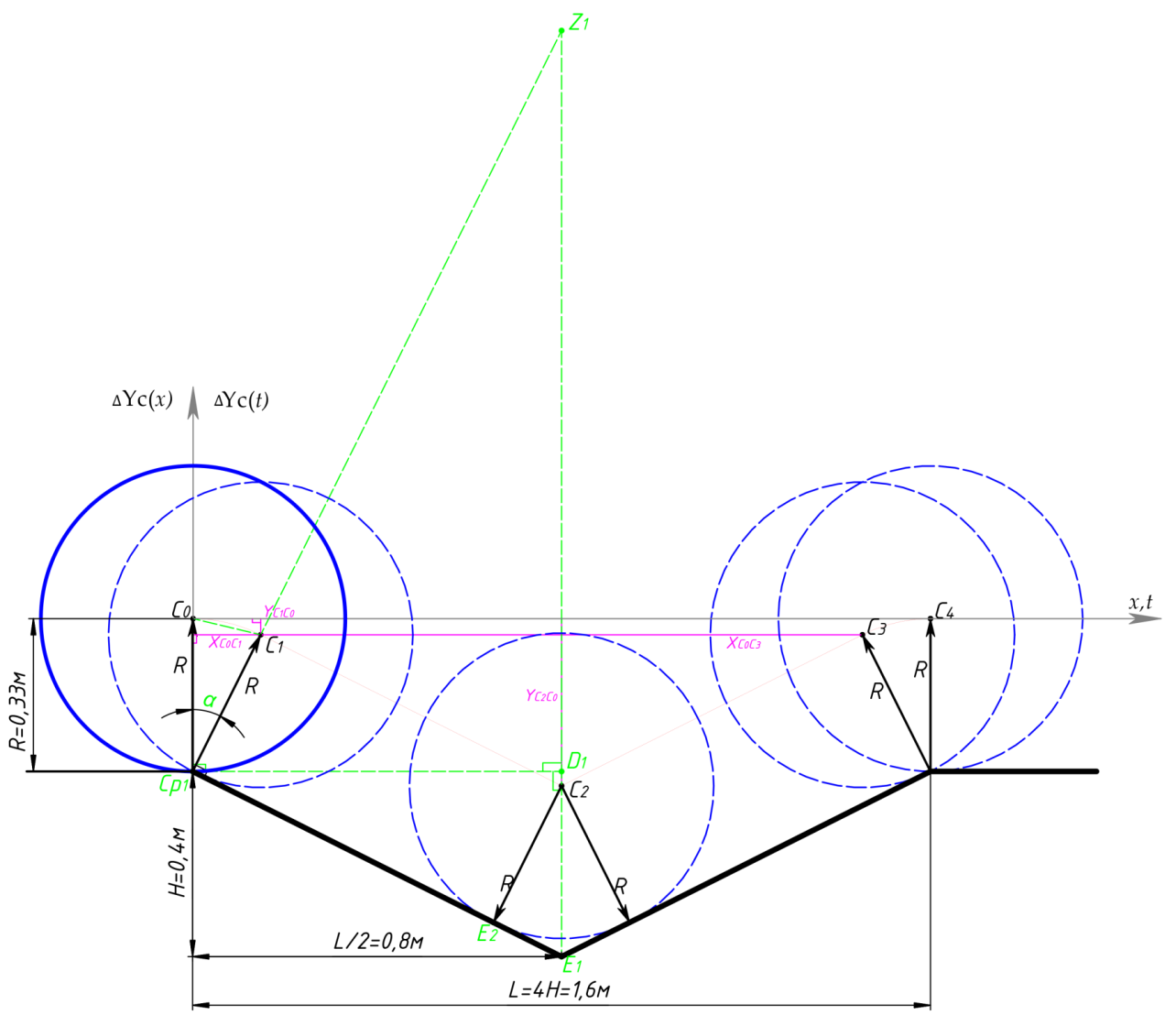
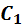 :
:  2)
2)  ;
;  ;
; 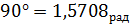
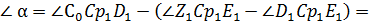
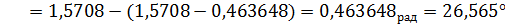 3)
3) 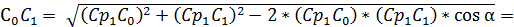
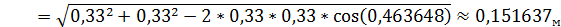 4)
4) 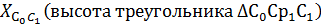
 5) По теореме Пифагора
5) По теореме Пифагора 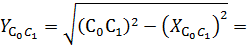
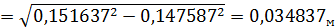
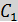 (
( )
)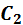 :
: 
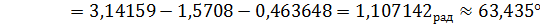 По теореме синусов
По теореме синусов  7)
7) 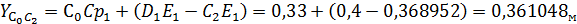 8)
8) 
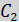 (
( )
)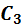 :
:  10)
10) 
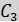 (
(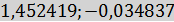 )
) :
: 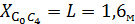 12)
12) 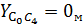
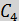 (
(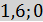 )
)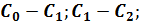
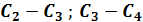
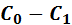 :
: 2)
2) 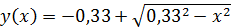
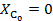

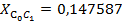
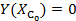

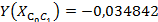
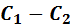 :
: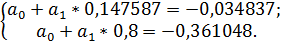 4)
4) 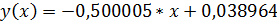
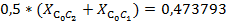
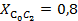
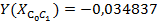
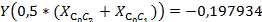
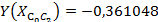
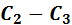 :
: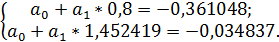 6)
6) 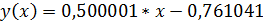

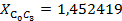

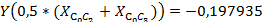
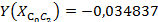
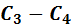 :
: 8)
8) 
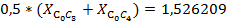

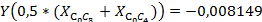
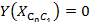
 составим таблицу в MicrosoftExcel и построим график траектории движения центра жесткого колеса.
составим таблицу в MicrosoftExcel и построим график траектории движения центра жесткого колеса.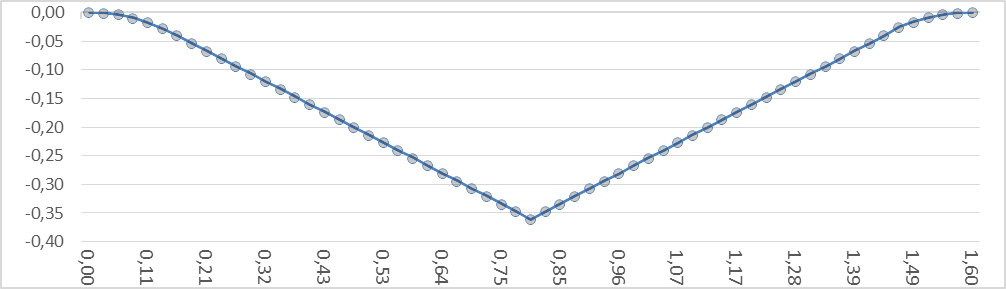

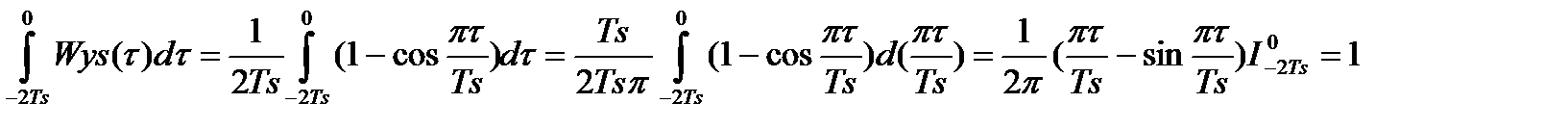
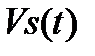 упругого колеса запаздывает на время Ts – эффективное время сглаживания(с помощью этого моделируется пневматическая шина).
упругого колеса запаздывает на время Ts – эффективное время сглаживания(с помощью этого моделируется пневматическая шина).


